2.5 波前动态
Vytvoření vlnoplochy
Jednoměničový snímač lze považovat za pístový zdroj, kde jediný disk nebo deska stlačuje zkušební médium a který generuje vlnu, již lze matematicky popsat jako součet vln od velkého počtu bodových zdrojů. Tato úvaha vychází z Huygensova principu, který v sedmnáctém století zformuloval holandský fyzik Christian Huygens a který říká, že každý bod vlnoplochy, která se šíří prostorem, lze považovat za bodový zdroj vytvářející novou vlnu, jež má v prostoru kulový tvar, a že výsledná sjednocená vlnoplocha je součtem všech těchto jednotlivých kulových vln.
Rozptyl svazku
V zásadě se bude zvuková vlna generovaná snímačem šířit přímo, dokud nenarazí na hranici prostředí. Co se stane potom, je uvedeno dále. Je-li však dráha zvuku delší, než je vzdálenost blízkého pole, průměr svazku se bude zvětšovat a svazek se bude rozbíhat stejně, jako je tomu u světelného svazku vycházejícího z bodového zdroje. Úhel rozptylu svazku nezaostřeného snímače lze vypočítat následujícím způsobem:

Z této rovnice je vidět, že rozptyl svazku se zvětšuje, když frekvence klesá a průměr se zmenšuje. Vzhledem k tomu, že velké úhly rozptylu svazku mohou způsobit rychlý pokles akustické energie se vzdáleností, lze efektivní pokles citlivosti k malým reflektorům a odezvu odraženého signálu v oblastech použití s dlouhými dráhami zvuku zlepšit tím, že se využijí snímače s vyšší frekvencí, případně s větším průměrem.
Útlum
Uspořádaná vlnoplocha generovaná ultrazvukovým snímačem se při svém šíření prostředím v důsledku nedokonalého přenosu energie mikroskopickou strukturou jakéhokoliv materiálu začne rozbíjet. Uspořádané mechanické vibrace (zvukové vlny) se změní na náhodné mechanické vibrace (teplo) a k tomuto jevu bude docházet tak dlouho, dokud vlnoplocha nezanikne. Tento proces se označuje jako útlum zvuku.
Matematická teorie útlumu a rozptylu je složitá. Zmenšování amplitudy v důsledku útlumu podél dráhy zvuku bude dáno součtem absorpčních účinků, které rostou úměrně s frekvencí, a rozptylových účinků, které se mění ve třech zónách a závisí na poměru velikosti zrn na rozhraní nebo jiných objektů, na kterých dochází k rozptylu, vůči vlnové délce. Ve všech případech účinky rozptylu nabývají na závažnosti s rostoucí frekvencí. Daný materiál bude mít při dané teplotě a zkušební frekvenci konkrétní hodnotu koeficientu útlumu, která se běžně vyjadřuje v jednotkách neperů na centimetr (Np/cm). Jakmile je znám koeficient útlumu, lze vypočítat ztráty na dané dráze zvuku podle rovnice.

Vzhledem k tomu, že se jedná o praktickou záležitost, se koeficienty útlumu v oblastech použití ultrazvukového nedestruktivního testování (NDT) za normálních okolností spíše měří než vypočítávají. Vyšší frekvence budou v libovolném médiu zeslabovány rychleji než nižší frekvence, takže u materiálů s vysokým koeficientem útlumu, jako jsou plasty s nízkou hustotou nebo pryž, se obvykle používají nízké zkušební frekvence.
Odraz a průchod na kolmém rovinném rozhraní
Když se zvuková vlna při šíření médiem setká s rozhraním s jiným médiem, které leží kolmo na směr šíření vlny, část energie vlny se odrazí přímo zpět a část bude pokračovat přímo vpřed. Procento odražené energie v porovnání s procentem energie, která projde, bude záviset na akustické impedanci těchto dvou materiálů, přičemž akustická impedance je definována jako hustota materiálu vynásobená rychlostí zvuku. Koeficient odrazu na rovinném rozhraní, tedy procento akustické energie, které se odrazí zpět směrem ke zdroji, lze vypočítat následovně:

Z této rovnice je vidět, že čím jsou akustické impedance obou materiálů podobnější, tím více koeficient odrazu klesá, a čím jsou akustické impedance odlišnější, tím více koeficient odrazu roste. Podle teorie je odraz od rozhraní mezi dvěma materiály se stejnou akustickou impedancí roven nule a v případě materiálů s naprosto odlišnými hodnotami akustické impedance, jako je tomu například na rozhraní mezi ocelí a vzduchem, se koeficient odrazu blíží ke 100 %.
Lom a režim konverze vlny na jiných než kolmých rozhraních
Když zvuková vlna, která se šíří materiálem, narazí na rozhraní s jiným materiálem pod jiným úhlem než nula stupňů, část akustické energie se odrazí pod stejným úhlem, pod jakým na rozhraní dopadla. Současně dojde k tomu, že část energie vlny, která projde do druhého materiálu, se zlomí podle Snellova zákona, což je skutečnost, která byla nezávisle odvozena přinejmenším dvěma matematiky v sedmnáctém století. Snellův zákon dává do souvislosti siny dopadajícího a lomeného úhlu s rychlostmi vlny v každém z materiálů, jak je přehledně uvedeno níže.
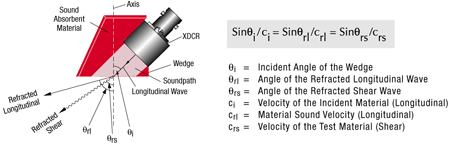
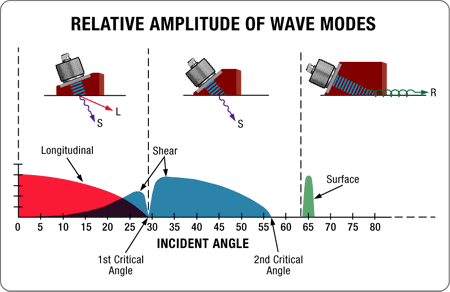
Je-li rychlost zvuku v druhém médiu vyšší než v prvním, pak kromě ohybu, jehož výpočet je vysvětlen výše, dojde ke změně režimu, a to nejčastěji z režimu podélné vlny na režim příčné vlny. Tento jev využívají postupy pro kontrolu pomocí úhlového svazku. Když úhel dopadu v prvním médiu (kde se zvuk šíří pomaleji), jako je například klín nebo voda, roste, úhel lomené podélné vlny ve druhém materiálu (kde se zvuk šíří rychleji), jako je například kov, také poroste. Když se úhel lomené podélné vlny přiblíží k 90 stupňům, stále větší část akustické energie se bude přeměňovat na příčnou vlnu s nižší rychlostí, která se zlomí pod úhlem daným Snellovým zákonem. Při úhlech dopadu větších, než které by vedly k úhlu lomu podélné vlny většímu než 90 stupňů, lomené vlny existují pouze v režimu příčné vlny. Ještě větší úhel dopadu povede k situaci, kdy teoreticky dojde k lomu příčné vlny pod úhlem 90 stupňů, přičemž v druhém materiálu se vygeneruje povrchová vlna. Diagram níže uvádí tento účinek pro typickou sestavu úhlových svazků s vazebním prostředkem do oceli.