Autoři: Nicolas Badeau, Guillaume Painchaud-April a Chi-Hang Kwan
Shrnutí
V současné době je technika úplné fokusace (TFM) používaná k provádění kontrol zahrnuta v regulačních předpisech a normách vztahujících se na oblast nedestruktivního zkoušení (NDT), například v předpisu ASME, část V. Jedním z důležitých parametrů specifikovaných v těchto předpisech pro plánování snímání technikou TFM je věrnost amplitudy. Věrnost amplitudy je definována jako změna amplitudy získaná pro specifikovaný reflektor, přináležící ke konečnému rozlišení zobrazovací mřížky. Typická přípustná mezní -prahová hodnota věrnosti amplitudy v těchto předpisech je maximálně 2 dB. Zatímco ve zmíněných předpisech jsou popsány experimentální metody měření věrnosti amplitudy daného nastavení, v tomto článku se věnujeme tradiční analytické metodě. Při odhadu věrnosti amplitudy je uváženo také použití TFM obálky, protože to umožňuje použít méně hustou TFM mřížku, aniž by přitom tento postup vedl k překročení hodnoty věrnosti amplitudy nad stanovenou toleranci. U standardního TFM zobrazování empirické výsledky ukázaly, že pro dosažení věrnosti amplitudy nižší než 2 dB je potřeba rozlišení mřížky přibližně λ0/10. U TFM zobrazování s obálkou empirické výsledky ukázaly, že pro dosažení hodnot vyhovujících předpisům je potřeba rozlišení mřížky λ0/3,3.
Úvod
Technika úplné fokusace (TFM) je nově přijatá technika nedestruktivního zkoušení součástek a dílů (NDT). Normy a regulační předpisy, například ASME V [1], začlenily techniku snímání úplnou maticí (FMC) a techniku TFM jako další techniky ultrazvukového zkoušení metodou phased array. I když v oblasti nedestruktivního zkoušení jsou techniky FMC a TFM relativní novinkou, již nějakou dobu jsou využívány při ultrazvukovém zobrazení ve zdravotnických aplikacích jako zlatý standard lékařského zobrazování ultrazvukem [2–4]. Ve skutečnosti je většina lékařských technik zobrazování pomocí ultrazvuku porovnávána se zobrazováním technikou TFM.
I když existuje několik technik podobných technikám FMC/TFM (např. VTFM [5], IWEX [6], SAFT [7]), nejčastěji používaným algoritmem zpracování je algoritmus zpoždění a sčítání [2–4, 8, 9]. Technika FMC/TFM spočívá ve schématu pořizování dat (FMC), které spoléhá na pořízení signálu ze všech kombinací vysílacích a přijímacích elementů, a schématu sčítání (TFM), kterým se vypočte výsledek fokusovaného ultrazvukového svazku ve větším počtu míst v oblasti zájmu. Oblast zájmu TFM se často překrývá karteziánskou mřížkou, přičemž jednotlivé body protnutí, do kterých je aplikováno akustické zaostření, se nazývají pixely. Metoda zaostřování je podobná standardnímu zobrazování ultrazvukem technikou phased array, s tou výjimkou, že svazky jsou tvarovány při následném zpracování za použití dat uložených v datové matici FMC. Proces zpoždění a sčítání, který následuje po pořízení dat, vychází z předpokladu linearity základních akustických vln, jak je nalézáme při typických použitích nedestruktivního zkoušení.
Na techniku FMC/TFM lze nahlížet jako na přirozené rozšíření konvenční techniky phased array. Nicméně je třeba vzít v úvahu nové parametry nastavení, a to z důvodu rozdílů v reprezentaci dat ve srovnání s ultrazvukovým zkoušením konvenční technikou phased array (PAUT). Jedním takovým konceptem je věrnost amplitudy (amplitude fidelity – AF) TFM mřížky. Věrnost amplitudy je definována jako maximální změna amplitudy indikace způsobená rozlišením TFM mřížky {Δx, Δz}. Po zbývající část této studie je uvažováno použití uniformní karteziánské mřížky, tj. (Δx = Δz). Věrnost amplitudy lze formálně vyjádřit jako
![(Rov. 1) AF(Δx)≡-20 log〖(A_(vzorkované maximum) (Δx))/A_(skutečné maximum) 〗 [dB]](https://industrial.evidentscientific.com.cn/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_01.jpg?rev=43A1)
kde Avzorkované maximum je změřená maximální amplituda zájmové vlastnosti na základě vzorkování konečné mřížky a Askutečné maximum je maximum té samé vlastnosti na základě mřížky s nekonečným rozlišením. Mezní případ, kdy velikost mřížky ve dvou osách nabývá nulové hodnoty pro Avzorkované maximum (Δx), definuje Askutečné maximum a příslušná věrnost amplitudy nabývá hodnotu 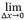 AF(Δx)=0. Rovnice 1 představuje formální definici pro výpočet věrnosti amplitudy s ohledem na rozlišení mřížky. Nicméně v praxi lze skutečné maximum Askutečné maximum základního signálu pouze odhadovat převzorkováním obrazu TFM amplitudy a interpolací.
AF(Δx)=0. Rovnice 1 představuje formální definici pro výpočet věrnosti amplitudy s ohledem na rozlišení mřížky. Nicméně v praxi lze skutečné maximum Askutečné maximum základního signálu pouze odhadovat převzorkováním obrazu TFM amplitudy a interpolací.
![(Rov. 2) (AF) ̂(Δx)=-20 log〖(A_(vzorkované maximum) (Δx))/A ̂_(skutečné maximum) 〗 [dB]](https://industrial.evidentscientific.com.cn/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_02.jpg?rev=43A1)
kde  skutečné maximum je odhad hodnoty Askutečné maximum.
skutečné maximum je odhad hodnoty Askutečné maximum.
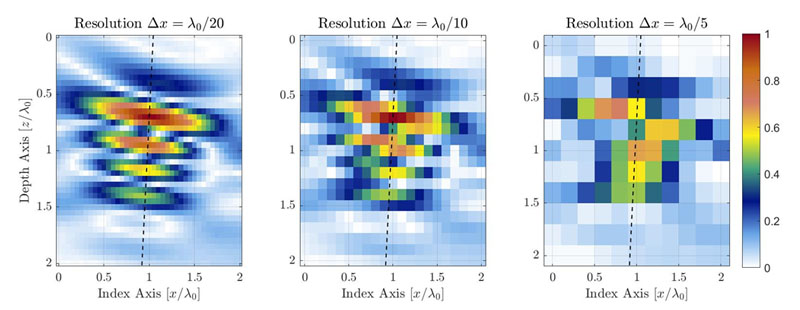
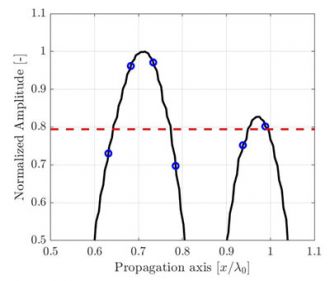
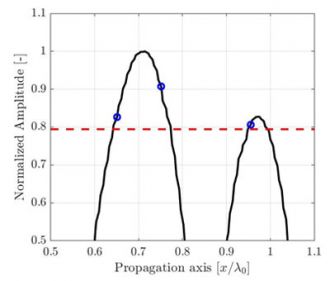
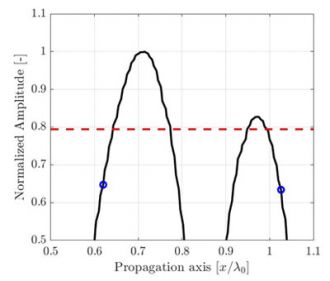
Obrázek 1. Ilustrace zhoršování kvality TFM obrazu způsobené snižováním rozlišení TFM mřížky. Čárkovaná čára představuje hlavní osu šíření akustických vln.
Pro identickou oblast zájmu má mřížka s hrubším rozlišením menší počet pixelů. Obrázek 1 ukazuje typické TFM obrazy téhož bočního vývrtu (SDH) při různých hodnotách rozlišení mřížky. Rozlišení mřížky je definováno jako zlomek vlnové délky střední frekvence sondy λ0= c/f0, kde c je rychlost šíření akustických vln v dílu a f0 je střední frekvence sondy.
Normy a regulační předpisy v současnosti obsahují požadavek, aby věrnost amplitudy byla nejvýše 2 dB [1,10]. Tento požadavek povstává z praktického kompromisu mezi dostatečnou kvalitou obrazu, při které lze stále ještě zajistit náležitou analýzu nedestruktivního zkoušení, a produktivitou provádění kontrol, na kterou má velký dopad hustota TFM mřížky v dané oblasti zájmu. Upozorňujeme, že vyváženost mezi kvalitou TFM obrazu a produktivitou provádění kontroly je kriticky důležitá zejména v případě samostatných přenosných zařízení, která nemají přístup k výkonu potřebnému ke zpracování velkého množství dat. Očekává se, že se zlepšováním výkonnosti zabudovaného hardwaru a zvyšováním dostupnosti provádění vzdálených výpočtů tento problém časem vymizí.
I když byly navrženy některé empirické metody [10–12], jejich použití obvykle vyžaduje provádění rozsáhlých výpočtů a získané výsledky nepředstavují, v důsledku rozlišení mřížky, skutečnou amplitudu, což je problém, který bude vysvětlen v následující části. V tomto článku je představen způsob, jak precizně odhadnout věrnost amplitudy TFM nastavení, který technikům nedestruktivního zkoušení pomůže provádět produktivní kontroly a přitom zachovat shodu s předpisy.
Článek je rozdělen následovně: Nejdříve je uvedeno všeobecné vysvětlení problému, kterému technici NDT čelí. Následně je popsána metoda, jak empiricky změřit věrnost amplitudy TFM nastavení. V další části je navržen analytický model pro odhad věrnosti amplitudy. Navržený model je pak porovnán s empirickými měřeními ve třech různých případech použití TFM. Celá práce je pak shrnuta ve stručném závěru.
Řešený problém
I když lze použitím velmi jemné (tj. husté) mřížky dosáhnout velmi malých hodnot věrnosti amplitudy, elektronická zařízení, která dokáží provádět výpočty živých TFM obrazů, jsou stále omezena svými výpočetními limity. Jemnější rozlišení mřížky přes danou oblast zájmu znamená, že do výpočtu musíme zahrnout velký počet zaostřených bodů, což vede ke snížení produktivity kontroly a ke zpomalení mechanického snímání. NDT technik musí být schopen vybrat vhodné rozlišení mřížky, při kterém maximalizuje produktivitu kontroly, avšak stále zachová shodu s předpisy.
Věrnost amplitudy lze ilustrovat jednoduchým jednodimenzionálním vzorkem signálu v různých intervalech. Na příkladu zobrazeném na obrázku 2 je zobrazeným jednodimenzionálním signálem amplituda bočního vývrtu uvedeného na obrázku 1 spolu s osou šíření akustických vln, které jsou pořízeny z obrazu s vysokým rozlišením λ0/100. Pro účely příkladu je zobrazena pouze přiblížená (zvětšená) část v blízkosti maximální amplitudy signálu. I zde jsou měření při třech různých rozlišeních λ0/20, λ0/10 a λ0/5 označena modrým kroužkem přes velké rozlišení a je interpolována referenční hodnota (plná černá čára).
(a) Diskrétní rozlišení mřížky je λ0/20 a vypočítaná věrnost amplitudy je AF = 0,27 dB. |
(b) Diskrétní rozlišení mřížky je λ0/10 a vypočítaná věrnost amplitudy je AF = 0,82 dB. |
(c) Diskrétní rozlišení mřížky je λ0/5 a vypočítaná věrnost amplitudy je AF = 3,7 dB. |
Obrázek 2. Ilustrace účinku periody vzorkování na zaznamenanou amplitudu spolu s osou šíření vyznačenou na obr. 1. Interpolovaný referenční signál s vysokým rozlišením (černá čára) je zobrazen jako vizuální pomůcka. Věrnost amplitudy o hodnotě 2 dB, kterou vyžadují předpisy, je zobrazena červenou čárkovanou čarou.
Očividný závěr je, že hustší mřížka poskytuje lepší reprezentaci kontinuálního signálu, jak je kvantifikováno podle hodnoty AF z rovnice 1, avšak problém optimalizace přetrvává: Jaká je maximální velikost mřížky (Δxmax) zaručující, pro všechny možné polohy mřížky na TFM obraze, věrnost amplitudy  , která je rovna cílové hodnotě AFcíl? Neboli,
, která je rovna cílové hodnotě AFcíl? Neboli,
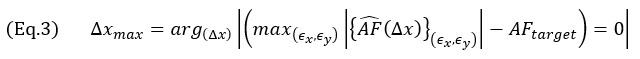
Z tohoto vyjádření problému je zřejmé, že pro získání maximální  pro pevnou velikost buňky (Δx) se musí vzít v úvahu všechny translace mřížky, identifikované posunutími (ϵx, ϵy). To proto, aby byly pokryty všechny možné případy umístění mřížky pro výpočet TFM obrazu.
pro pevnou velikost buňky (Δx) se musí vzít v úvahu všechny translace mřížky, identifikované posunutími (ϵx, ϵy). To proto, aby byly pokryty všechny možné případy umístění mřížky pro výpočet TFM obrazu.
V následující části je uvedena ilustrace principu měření pro soubor hodnot věrnosti amplitudy vygenerovaných několika posunutími mřížky { (Δx)}(ϵx, ϵy).
(Δx)}(ϵx, ϵy).
Empirické měření věrnosti amplitudy
Předtím než uvedeme, jak lze věrnost amplitudy odhadnout pomocí jednoduchého analytického modelu, je důležité definovat, jak lze věrnost amplitudy měřit v případě TFM obrazu experimentálně. V oboru nedestruktivního zkoušení bylo popsáno a navrženo několik technik [10–12], některé z nich však nekvantifikují věrnost amplitudy úplným způsobem. Empirické měření věrnosti amplitudy se pro techniky NDT může rychle stát velkou zátěží z hlediska pořizování dat, protože je zapotřebí provést výpočet velkého množství TFM obrazů z několika přesných poloh TFM mřížky.
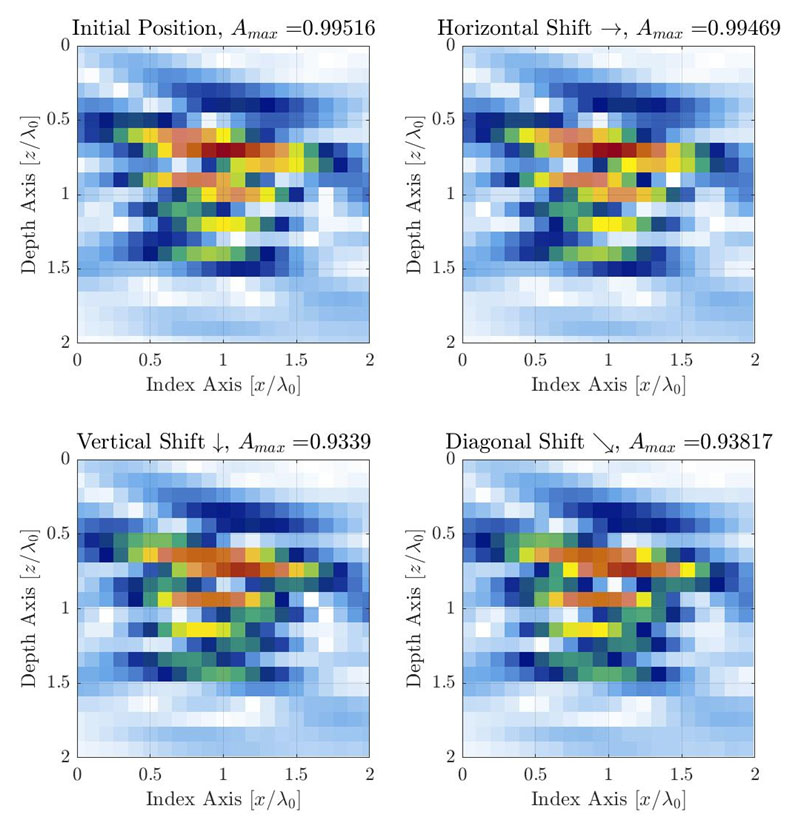
Obrázek 3. Ilustrace změn AF způsobených diskrétním rozlišením mřížky při posunutí mřížky ve 3 různých směrech. Rozlišení mřížky je nastaveno na Δx=Δy=λ0/10. Mřížka je posunuta o jednu čtvrtinu velikosti buňky mřížky doprava (ϵx=λ0/40, ϵy=0) (nahoře vpravo), dolů (ϵx=0, ϵy=λ0/40) (dole vlevo) a úhlopříčně (ϵx=λ0/40, ϵy=λ0/40) (dole vpravo).
Při typických použitích techniky TFM se jako referenční vada pro kalibraci amplitudy a měření věrnosti amplitudy používá boční vývrt [1,10]. Pozorovaná amplituda se nejvíce mění podél hlavní osy šíření akustických vln, což je funkce sondy, klínu a cílové polohy v oblasti zájmu (tj. polohy TFM mřížky relativně vůči sondě). V případě ilustrovaném na obrázku 1 je hlavní osa šíření akustického signálu téměř svislá. Nicméně v případě generické metody měření se bude osa šíření lišit v závislosti na lokaci v oblasti zájmu. U TFM obrazu je nutné k zachycení skutečné změny amplitudy způsobené diskrétností mřížky posunout vzorkovací mřížku ve všech směrech. Tento proces je ilustrován níže se stejným příkladem, jako je příklad na obrázku 1 (uprostřed), kde je rozlišení mřížky λ0/10.
Je doporučeno posunout mřížku o zlomek zkoušeného rozlišení mřížky (např. přibližně o jednu dvacetinu rozlišení) v každém směru; to je nutné, aby bylo dosaženo překrytí mřížky. To znamená, že k pokrytí posunutí jednoho rozlišení mřížky ve dvou ortogonálních směrech, je nutné vykonat celkem 202 = 400 kroků posunutí (používáme-li doporučený krok mřížky o hodnotě jedné dvacetiny rozlišení). Pro každé posunutí mřížky se zaznamená maximální amplituda a maximální a minimální zaznamenaná hodnota se použijí k získání věrnosti amplitudy pomocí rovnice 2. V příkladě uvedeném na obrázku 3 je rozlišení mřížky λ0/10 a změřená věrnost amplitudy je 0,88 dB. Pokud je tento ruční proces pro techniky NDT posuzován z pohledu potřebného počtu posunutí, je relativně těžkopádný a časově náročný. Znamená to také, že pro změření věrnosti amplitudy by muselo být spočítáno celkem 400 TFM obrazů jednoho rozlišení mřížky.
Stojí za to zmínit, že použitím softwarového posunutí polohy TFM mřížky relativně vůči sondě namísto mechanického posunutí sondy relativně vůči dílu, jak je navrženo v normě ASME, část V [12], je možné vygenerovat větší počet TFM obrazů pomocí jediné FMC datové sady. Další výhodou tohoto přístupu je možnost přístupu ke svislým složkám mřížky. Ve skutečnosti není možné mechanicky posunovat sondu a klín relativně vůči zvolenému bočnímu vývrtu ve směru hloubkové osy.
Některé přístroje NDT poskytují poloautomatizované nástroje, které posunou TFM mřížku, zaznamenají maximální amplitudu v oblasti zájmu a nakonec vypočítají výslednou věrnost amplitudy [11]. Nicméně tyto nástroje obvykle provádí posun pouze ve vodorovném směru a v důsledku toho věrnost amplitudy podhodnocují. Pro srovnání, jestliže je mřížka posouvána výhradně ve směru vodorovné osy, pro příklad ilustrovaný na obrázku 3, je změřená věrnost amplitudy 0,06 dB, což je více než 15krát nižší hodnota, než je změřená hodnota věrnosti amplitudy při uvážení svislé osy.
Fenomenologický model pro odhad věrnosti amplitudy
V této části je navržen jednoduchý analytický model založený na empirickém pozorování. Tento fenomenologický model bere v úvahu chování signálu podél hlavní osy šíření, u kterého se předpokládá, že obsahuje nejvíce fluktuací amplitudy, a tudíž je na rozlišení mřížky nejcitlivější. Obrázek 4 ukazuje empirický profil výsledného TFM obrazu bočního vývrtu podél hlavní osy šíření (modře) a podél boční osy svazku (červeně). Počátek osy je umístěn ve zřejmém umístění maxima amplitudy reprezentace obálky, což vysvětluje malý posun ve směru osy  pro reprezentaci oscilací. Poskytnuty jsou profily pro standardní oscilační TFM a pro TFM obálku.
pro reprezentaci oscilací. Poskytnuty jsou profily pro standardní oscilační TFM a pro TFM obálku.
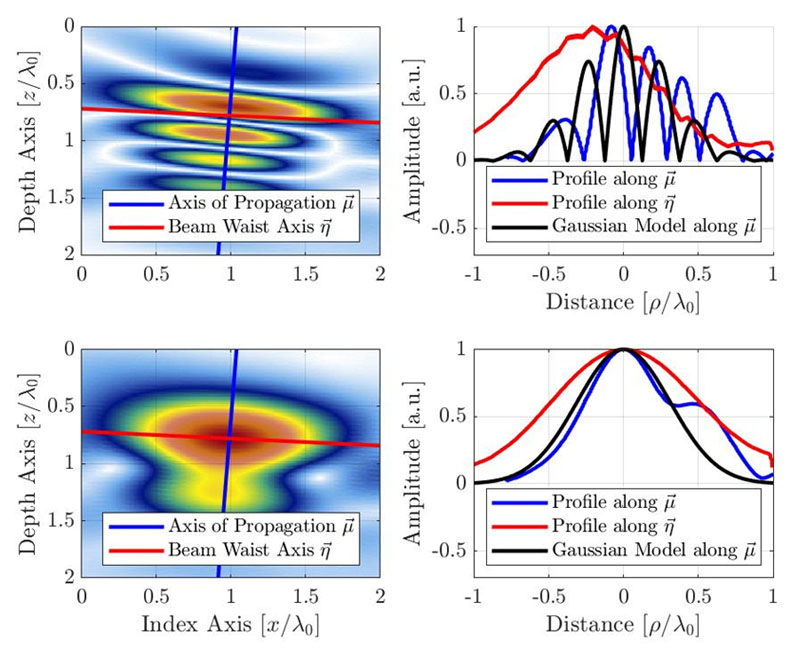
Obrázek 4. TFM obraz (nahoře: oscilační, dole: obálka) s profilem signálu podél osy šíření akustických vln a boční osy svazku. Navržený gaussovský model je ilustrován také pro obraz oscilační TFM a obraz TFM obálky. Všimněte si, že zřejmá vlnová délka je půlena z důvodu vlastní podstaty impulz–echo tvarování TFM svazku.
Jak již bylo uvedeno dříve, předpokládá se, že osou, v jejímž směru dochází k největším změnám amplitudy, je hlavní osa šíření akustických vln. Proto model cílí na změny amplitudy v tomto směru. Modelovým signálem je kosinově modulovaná gaussovská křivka
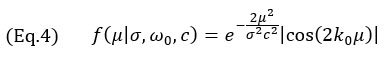
kde k0=ω0/c je vlnové číslo při střední úhlové frekvenci ω0 sondy, σ je šířkový parametr závislý na střední frekvenci a relativní šířce pásma bw. Šířkový parametr σ se vypočítá pomocí rovnice
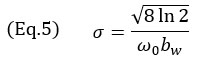
U typické NDT phased array sondy se relativní šířka pásma blíží 60 % označení, proto je v modelu použita hodnota (bw=0,6). Tím dojde k tomu, že gaussovská obálka je větší než jedna kosinová oscilace. Stojí za to zmínit, že střední frekvence kosinového členu v rovnici 3 je zdvojenou střední frekvencí sondy. To je dáno podstatou TFM zobrazování impulz–echo (dráha vysílaného signálu a dráha přijímaného signálu) a je možné toto pozorovat ve vzdálenosti mezi oscilacemi na obrázku 4. Konverzi mezi časovou doménou a prostorovou doménou lze zapsat jako μ = tc/2. To také vysvětluje faktor 2 použitý jako exponenciální člen v rovnici 3.
Pro oscilační model rovnice 4, protože gaussovská obálka je mnohem větší než jedna oscilace kosinové funkce, jsou uvažovány pouze hodnoty |μ|≤λ0/8, protože větší hodnoty vytvářejí efekt prostorového aliasingu věrnosti amplitudy.
Pro model TFM obálky se použije jen gaussovský člen rovnice 4, což vede k následující rovnici
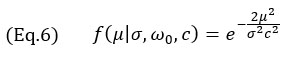
platné pro jakékoli rozlišení mřížky. Profil získaný z modelu rovnic 3 a 7 je ilustrován na obrázku 4 spolu s experimentálními profily. Všimněte si, že empirická měření vykazují také signál povrchové vlny („wrap around“ echo, typické u bočních vývrtů) zpožďující se za hlavním echem. To je vlastnost, která se v navrženém modelu nevyskytuje.
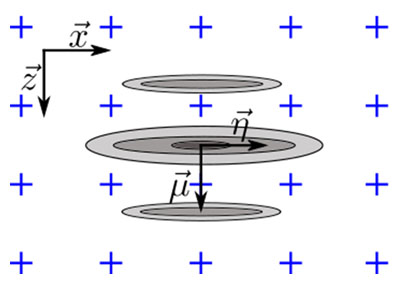
Musí se vzít v úvahu orientace vady relativně vůči ortogonálním osám mřížky, aby se v rámci modelu získal případ nejhoršího možného scénáře věrnosti amplitudy. Jak je ilustrováno na obrázku 5a, k nejhoršímu scénáři pro oscilační TFM dochází tehdy, když je hlavní osa šíření akustických vln  rovnoběžná s jednou z os mřížky. Odtud plyne, že věrnost amplitudy musí být vypočtena, jako kdyby maximum amplitudy bylo umístěno ve středu mezi dvěma body mřížky ve směru kterékoli osy
rovnoběžná s jednou z os mřížky. Odtud plyne, že věrnost amplitudy musí být vypočtena, jako kdyby maximum amplitudy bylo umístěno ve středu mezi dvěma body mřížky ve směru kterékoli osy 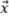 nebo
nebo 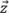 , výsledkem čehož je vztah
, výsledkem čehož je vztah
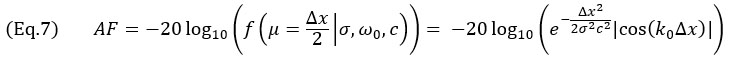
pro Δx≤λ0/4. V případě TFM obálky k nejhoršímu scénáři dochází v případě, kdy je profil amplitudy identický podél hlavní osy šíření  a boční osy svazku
a boční osy svazku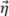 . Tento případ – ilustrovaný na obrázku 5b – odpovídá situaci, kdy je boční vývrt reprezentován jako kruh a tudíž hlavní osa šíření
. Tento případ – ilustrovaný na obrázku 5b – odpovídá situaci, kdy je boční vývrt reprezentován jako kruh a tudíž hlavní osa šíření  může mít jakoukoli orientaci. K nejhoršímu scénáři dochází v případě, kdy se echo bočního vývrtu nachází ve středu mezi dvěma sousedícími body, jak je ilustrováno na obrázku. V tomto případě se musí věrnost amplitudy vypočítat podél úhlopříčky mřížky, čímž se získá vztah
může mít jakoukoli orientaci. K nejhoršímu scénáři dochází v případě, kdy se echo bočního vývrtu nachází ve středu mezi dvěma sousedícími body, jak je ilustrováno na obrázku. V tomto případě se musí věrnost amplitudy vypočítat podél úhlopříčky mřížky, čímž se získá vztah
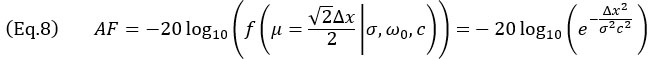
Aproximativní výraz pro hodnotu Δx s ohledem na AF, v případech, kdy je hodnota AF malá, což je typický případ použití NDT, lze získat pro oscilační model z rovnice 7,

a pro model obálky z rovnice 8,
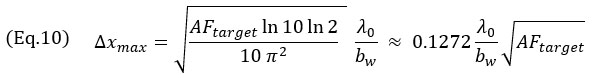
Ve všech případech tyto výrazy vyjadřují závislost velikosti mřížky na druhé odmocnině hodnoty AF. Rovnice 9 byla získána aproximací rovnice 7, rozvojem do Taylorovy řady druhého řádu. Tato aproximace je ilustrována na obrázku 6 spolu s exaktním modelem. Všimněte si také, že velikost mřížky v případě modelu oscilací je pro malá bw téměř nezávislá na relativní šířce pásma. Také stojí za to zmínit, že jak u oscilačního modelu, tak u modelu obálky je maximální rozlišení mřížky Δxmax ve vztahu s druhou odmocninou cílené věrnosti amplitudy. Tyto hodnoty reprezentují maximální rozlišení mřížky pro dosažení shody s předpisy na základě fenomenologického modelu.
(a) Scénář nejhoršího případu u oscilační TFM nastává, když je osa |
(b) Scénář nejhoršího případu pro TFM obálku nastává, když profil amplitudy podél |
Obrázek 5. Ilustrace orientace vady relativně vůči ortogonální ose mřížky pro nejhorší scénář pro (a) oscilační TFM a (b) TFM obálku.
Experimentální ověření
Navržený model byl ověřen pomocí empirických výsledků u tří různých případů kontrol technikou TFM. U všech tří nastavení TFM bylo několik bočních vývrtů zobrazeno s různými rozlišeními mřížky a byla změřena věrnost amplitudy podle dříve popsaného modelu. Parametry těchto tří případů použití jsou uvedeny v tabulce 1. Prvním případem je kontaktní měření s použitím vysokofrekvenční sondy (7,5 MHz), ve druhém případě byly použity smykové vlny při nízké frekvenci (5 MHz) a ve třetím případě byly použity smykové vlny při vyšší frekvenci sondy (10 MHz) a počty elementů. Ve všech případech se vývrty nacházely v rámci 50 mm od horní plochy měrky z uhlíkové oceli.
Tabulka 1: Parametry TFM nastavení použité k experimentálnímu ověření věrnosti amplitudy.
| Pouzdro | Parametry sondy | Parametry klínu | Parametry dílu | TFM režim | |||||
|---|---|---|---|---|---|---|---|---|---|
|
Frekvence
[MHz] |
Počet
[#] |
Rozteč
[mm] |
Rychlost
[m/s] |
Úhel
[°] |
Výška
[mm] |
Rychlost
cp – cs [m/s] |
SDH
Průměr [mm] | ||
| 1 | 7,5 | 64 | 1,0 | nevztahuje se | nevztahuje se | 0 | 3240 - 5890 | 1 | L-L |
| 2 | 5 | 32 | 1,0 | 2330 | 36,1 | 11,0 | 3240 - 5890 | 0,5 | T-T |
| 3 | 10 | 64 | 0,5 | 2330 | 36,1 | 11,0 | 3240 - 5890 | 1 | T-T |
Na obrázku 5 je znázorněna výsledná věrnost amplitudy pro standardní oscilační TFM (nahoře) a pro TFM obálku (dole). Každý jednotlivý šedý bod reprezentuje různou kombinaci případu použití, bočního vývrtu a rozlišení mřížky. Věrnost amplitudy odhadnutá pomocí dříve představeného gaussovského modelu je znázorněna černou plnou čarou. Červená čárkovaná čára odpovídá mezní hodnotě vyžadované předpisy, tedy hodnotě 2 dB.
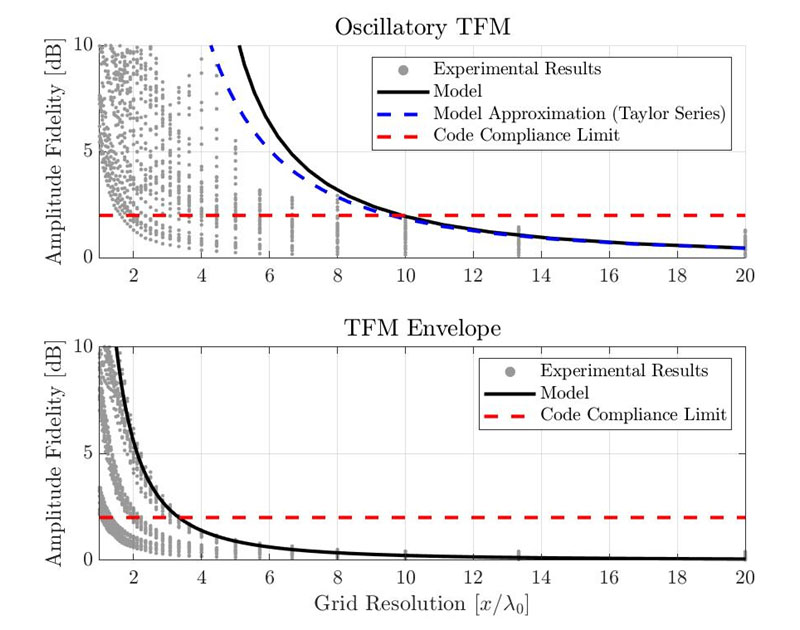
Obrázek 6. Srovnání empirických měření věrnosti amplitudy s výsledky navrhovaného gaussovského modelu pro standardní oscilační TFM (nahoře) a pro TFM obálku (dole).
Podle navrženého modelu je rozlišení potřebné k dodržení shody s předpisy λ0/9,9 pro oscilační TFM a λ0/3,3 pro TFM obálku. Experimentální výsledky ukazují, že minimální rozlišení mřížky pro dodržení shody s předpisy je kolem λ0/10 pro standardní oscilační TFM a λ0/3,3 pro TFM obálku. Všimněte si však, že tyto hodnoty byly vzaty z nejhorších prezentovaných experimentálních případů. Některé měřené hodnoty věrnosti amplitudy jsou nižší než 2 dB, a to i při hrubším rozlišení mřížky. Navržený model tedy poskytuje dobré, i když stále konzervativní odhady pro věrnost amplitudy TFM nastavení.
Závěr
Věrnost amplitudy TFM nastavení je důležitou mírou odolnosti zobrazení s ohledem na rozlišení mřížky. Čím je mřížka hustší, tím je hodnota věrnosti amplitudy nižší. Normy a regulační předpisy v současnosti zahrnují techniku úplné fokusace jako novou techniku pro provádění kontrol a vyžadují, aby hodnota věrnosti amplitudy byla 2 dB nebo méně. V tomto článku jsme představili, jak lze věrnost amplitudy korektně empiricky měřit, a jednoduchý analytický model pro odhad věrnosti amplitudy výsledků pro TFM nastavení.
Jednoduchý analytický model byl navržen na základě profilu amplitudy podél hlavní osy šíření akustických vln. Model odhaduje profil amplitudy jako gaussovské modulované kosinové oscilace. Použití tohoto profilu k odhadům věrnosti amplitudy vede k dobrým výsledkům pro standardní oscilační TFM i pro TFM obálku. Empirické výsledky ukázaly, že pro rozlišení mřížky je potřeba pro standardní oscilační TFM hodnota do λ0/10, resp. pro TFM obálku λ0/3,3. Navržený analytický model odhaduje jako potřebné rozlišení mřížky hodnotu λ0/9,9 pro standardní TFM a λ0/3,3 pro TFM obálku. Navržený model by tudíž mohl být používán k odhadu věrnosti amplitudy TFM nastavení.
Chcete-li se dozvědět více o výhodách použití TFM obálky jako součásti řešení vyhovujícího předpisům, přečtěte si naši bílou knihu „Použití techniky úplné fokusace s funkcí obálky.“
Literatura
[1] ASME Committee, 2019, „ASME BPVC.V Article 4 Mandatory Appendix XI Full Matric Capture“.
[2] Oralkan, O., Ergun, A. S., Johnson, J. A., Karaman, M., Demirci, U., Kaviani, K., Lee, T. H., and Khuri-Yakub, B. T., 2002, „Capacitive Micromachined Ultrasonic Transducers: Next-Generation Arrays for Acoustic Imaging?“, IEEE Trans. Ultrason., Ferroelect., Freq. Contr., 49(11), pp. 1596–1610.
[3] Thomenius, K. E., 1996, „Evolution of Ultrasound Beamformers“, 1996 IEEE Ultrasonics Symposium. Proceedings, IEEE, San Antonio, TX, USA, pp. 1615–1622.
[4] Freeman, S., Li, P., and O’Donnell, M., „Retrospective Dynamic Transmit Focusing“, p. 24.
[5] Wilcox, P. D., 2006, „Exploiting the Full Data Set from Ultrasonic Arrays by Post-Processing“, AIP Conference Proceedings, AIP, Brunswick, Maine (USA), pp. 845–852.
[6] Portzgen, N., Gisolf, D., and Blacquiere, G., 2007, „Inverse Wave Field Extrapolation: A Different NDI Approach to Imaging Defects“, IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 54(1), pp. 118–127.
[7] Sharpe, R. S., ed., 1982, Research Techniques in Nondestructive Testing. Vol. 6: ..., Acad. Press, London.
[8] Holmes, C., Drinkwater, B. W., and Wilcox, P. D., 2008, „Advanced Post-Processing for Scanned Ultrasonic Arrays: Application to Defect Detection and Classification in Non-Destructive Evaluation“, Ultrasonics, 48(6–7), pp. 636–642.
[9] Holmes, C., Drinkwater, B. W., and Wilcox, P. D., 2005, „Post-Processing of the Full Matrix of Ultrasonic Transmit–Receive Array Data for Non-Destructive Evaluation“, NDT & E International, 38(8), pp. 701–711.
[10] ISO, 2020, „ISO/DIS 23865 -FMC-TFM - General Use of TFM-FMC Technique“.
[11] Johnson, P., 2019, „With a New Software Wizard, There’s No Sorcery but the Magic of the M2M Gekko Is Evident with Instant Code Compliance for Your TFM Weld Inspections.“, Code Compliant TFM Weld Inspection with Three Clicks.
[12] ASME Committee, 2019, „ASME BPVC.V Article 4 Nonmandatory Appendix F - Examination of Welds Using Full Matrix Capture“.