2.5 波前动态
Wellenfrontbildung
Man kann sich einen Einzelschwinger-Prüfkopf wie einen elastischen Körper vorstellen, der seine Energie an das zu prüfende Material überträgt. Die so erzeugte Schallwelle wird entsprechend dem Huygensschen Prinzip mathematisch als Summe der Wellen einer großen Anzahl Ausgangspunkte errechnet. Dieses Prinzip, das zuerst im 17. Jahrhundert vom niederländischen Physiker Christiaan Huygens aufgestellt wurde, besagt, dass jeder Punkt einer sich ausbreitenden Wellenfront der Ausgangspunkt einer neuen kugelförmigen Welle ist, und dass die daraus entstehende vereinte Wellenfront die Summe aller einzelnen kugelförmigen Wellen darstellt.
Schallbündelausbreitung
Im Prinzip breitet sich eine von einem Schallkopf erzeugte Schallwelle in gerader Linie aus, bis sie auf eine Materialgrenze stößt. Was dann passiert, wird im folgenden Diagramm erklärt. Ist jedoch der Schallweg länger als das Nahfeld, vergrößert sich der Durchmesser des Schallbündels wie der Lichtkegel eines Scheinwerfers. Der Winkel der Schallbündelausbreitung eines nicht fokussierten Schallkopfs wird wie folgt berechnet:

Aus dieser Gleichung ist ersichtlich, dass die Schallbündelausbreitung bei niedrigeren Frequenzen und kleineren Durchmesser zunimmt. Da ein großer Ausbreitungswinkel des Schallbündels dazu führen kann, dass die Schallenergie pro Flächeneinheit mit der Entfernung schnell abnimmt, wodurch die Empfindlichkeit gegenüber kleinen Reflektoren effektiv verringert wird, kann das Echoansprechen in einigen Anwendungsbereichen mit langen Schallwegen durch den Einsatz eines Schallkopfes mit höherer Frequenz und/oder größerem Durchmesser verbessert werden.
Schallschwächung
Bei der Ausbreitung in einem Medium zerfällt aufgrund einer unvollkommenen Energieübertragung durch die Mikrostruktur des Materials allmählich die von einem Ultraschallkopf erzeugte organisierte Wellenfront. Geordnete mechanische Schwingungen (Schallwellen) verwandeln sich in willkürliche mechanische Schwingungen (Hitze), bis die Wellenfront nicht mehr erkennbar ist. Diesen Vorgang nennt man Schallschwächung.
Die mathematische Theorie der Schallschwächung und der Schallstreuung ist komplex. Der Amplitudenverlust eines gegebenen Schallwegs ist die Summe der Absorptionseffekte, die linear mit der Frequenz zunehmen, und der Streuungseffekte, die über drei Bereiche in Abhängigkeit vom Verhältnis der Wellenlänge zur Korngrößengrenze oder von anderen Streuungsfaktoren variieren. In jedem Fall erhöht sich der Streuungseffekt mit der Frequenz. Jedes bei gegebener Temperatur mit gegebener Frequenz geprüfte Material besitzt einen spezifischen Schallschwächungskoeffizienten, der üblicherweise in Neper pro Zentimeter (Np/cm) angegeben wird. Ist der Schwächungskoeffizient bekannt, kann der Verlust auf einem gegebenen Schallweg mit folgender Gleichung berechnet werden:

In der Praxis wird in der zerstörungsfreien Ultraschallprüfung der Schwächungskoeffizienten eher gemessen als berechnet. Hohe Frequenzen werden in jedem Medium schneller geschwächt als niedrige, weswegen üblicherweise niedrige Prüffrequenzen bei Werkstoffen mit hohen Schwächungskoeffizienten, wie Kunststoffen mit geringer Dichte und Kautschuk, eingesetzt werden.
Reflexion und Transmission an senkrecht aufeinander treffenden Grenzen
Bei der Schallwellenausbreitung in einem bestimmten Medium und dem Auftreffen der Schallwelle auf die Grenzen zu einem anderen senkrecht zur Wellenrichtung liegenden Medium, wird ein Teil der Wellenenergie gerad zurückgeschallt und ein Teil breitet sich weiter geradlinig aus. Der Anteil an Reflexion und Transmission hängt von der akustischen Impedanz der zwei Materialien ab, wobei die akustische Impedanz als Materialdichte multipliziert mit der Schallgeschwindigkeit definiert wird. Der Reflexionskoeffizient an einer planaren Grenze (also der Prozentsatz der Schallenergie, der zur Schallquelle zurückreflektiert wird) kann folgendermaßen berechnet werden:

Aus dieser Gleichung ist ersichtlich, dass je ähnlicher die akustische Impedanz der beiden Materialien ist, desto kleiner ist der Reflexionskoeffizient, und je unterschiedlicher die akustische Impedanz ist, desto größer ist der Reflexionskoeffizient. Theoretisch ist die Reflexion an der Grenzfläche von zwei Materialien mit derselben akustischen Impedanz gleich null. Während im Fall von zwei Stoffen mit sehr verschiedener akustischer Impedanz, wie an der Grenze von Stahl und Luft, der Reflexionskoeffizent fast 100 % beträgt.
Brechung und Modenwandlung an nicht senkrecht aufeinander treffenden Grenzen
Breitet sich eine Schallwelle durch ein Material aus und trifft auf eine Grenze zu einem anderen Material unter einem anderen Winkel als Null, wird ein Teil der Wellenenergie nach vorne, in einem Winkel, der dem Einschallwinkel entspricht, reflektiert. Gleichzeitig wird der in das zweite Material geleitete Teil der Wellenenergie gemäß dem Snelliusschen Gesetz reflektiert. Dieses Gesetz wurde von mindestens zwei Mathematikern des 17. Jahrhunderts unabhängig voneinander aufgestellt. Das Snelliussche Gesetz definiert das Verhältnis des Sinus des Einschallwinkels und des reflektierten Winkels zur Ausbreitungsgeschwindigkeit der Schallwellen in beiden Materialien, wie im folgenden Diagramm gezeigt.
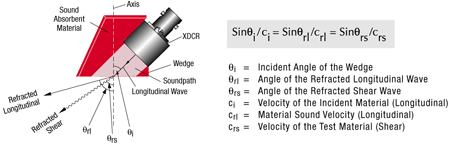
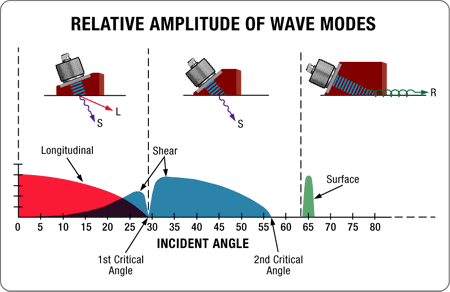
Ist die Schallgeschwindigkeit im zweiten Medium höher als im ersten, geht bei Winkeln oberhalb einer bestimmten Größe die Brechung mit einer Modenkonversion einher, meistens vom Longitudinalwellenmodus in den Transversalwellenmodus. Dies ist die Grundlage der weitverbreiteten Prüfmethode mit Schrägeinschallung. Mit Erhöhung des Einschallwinkels im ersten (langsameren) Medium (z. B. Vorlaufkeil oder Wasser) erhöht sich auch der Winkel der reflektierten Longitudinalwelle im zweiten (schnelleren) Medium (z. B. Metall). Mit Annäherung des Winkels der reflektierten Longitudinalwelle an 90° wird ein immer größerer Teil der Wellenenergie in Transversalwellen mit niedrigerer Geschwindigkeit umgewandelt, die im vorhergesehenen Winkel, nach dem Snelliusschen Gesetz, reflektiert werden. Bei größeren Einschallwinkeln, die eine mit 90° reflektierte Longitudinalwelle erzeugen würden, geht die gesamte reflektierte Welle in den Transversalmodus über. Bei noch größeren Einschallwinkeln, bei denen die Transversalwelle theoretisch mit 90° reflektiert würde, wird ein Punkt erreicht, in dem im zweiten Material eine Oberflächenwelle erzeugt wird. Das folgende Diagramm zeigt diesen Effekt für einen typischen Winkelschallkopf, der an Stahl gekoppelt ist.