包络功能使全聚焦方式更出色

Zusammenfassung

In diesem Artikel werden die Berechnung der Hüllkurve des TFM-Bilds (Total Focusing Method) und die Vorteile der Verwendung dieses optimierten TFM-Bilds als Teil einer normkonformen Lösung erklärt. Ein optimiertes TFM-Bild entsteht durch die Berechnung des Betrags von zwei verschiedenen TFM-Bildern: das erste TFM-Bild wird mithilfe der Standard-FMC-Funktion (Full Matrix Capture) berechnet und das zweite TFM-Bild mithilfe von FMC nach Hilbert-Transformation berechnet. Das entstandene TFM-Bild bietet eine bessere Grundlage für die Fehlergrößenbestimmung mit Amplitudenverfahren, da es bei gleicher Rasterauflösung weniger empfindlich gegenüber Amplitudenabweichungen ist als ein oszillatorisches Standard-TFM-Bild. Daher kann für das optimierte TFM-Bild eine gröbere Rasterauflösung eingestellt werden als für das oszillatorische Standard-TFM-Bild. Dies wiederum verringert den Gesamtaufwand der Berechnung und erhöht so die Erfassungsrate.

Einführung

TFM (Total Focusing Method) ist eine seit Kurzem anerkannte Methode zur zerstörungsfreien Prüfung von Material und Gefüge. Einige Standards und Normen umfassen nun einen Abschnitt zu FMC (Full Matrix Capture) und TFM (Total Focusing Method) für die zerstörungsfreie Prüfung (ZfP) [1], [2].

Einige ZfP-Geräte, wie das OmniScan X3 Prüfgerät ermöglichen eine TFM-Bildgebung in Echtzeit. Das TFM-Verfahren mittels FMC ist in den folgenden Abschnitten zusammengefasst. Grundsätzlich gilt, dass ein TFM-Bild die Summierung mehrerer Rohdaten der A-Bild-Amplituden ist. TFM-Bilder sind aufgrund des Ursprungs der Schallwellen für rohe A-Bilder oszillatorisch. Doch ZfP-Anwendungen basieren auch auf Amplitudentechniken, bei denen das Schwingungsverhalten als ein unerhebliches akustische Artefakt betrachtet wird. Häufig wird zur Anpassung des Schwingungsverhaltens in ZfP-Anwendungen die Amplitude bereinigt, sodass das Bild nur mit positiven Werten angezeigt wird. Dieser Ansatz kann die Interpretation eines optimierten Bildes, im Gegensatz zu einem vollständig oszillatorischen Bild, erleichtern. In diesem Artikel wird die Verwendung der Signalhüllkurve erläutert und wie sie die Fehlererkennung zunehmend verbessern sowie die Erfassungsrate bezüglich des oszillatorischen Standard-TFM-Bilds tatsächlich erhöhen kann.

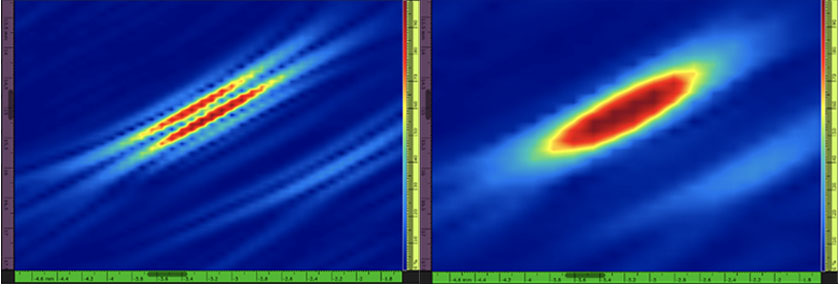
Abbildung 1: TFM-Bild einer Querbohrung (links) mit rein positiven Amplitudenwerten und Standard-TFM mit Signaloszillation. Die Rasterauflösung beträgt 0,08 mm (λ/8,1) bei einer max. Amplitude von 108,7 %. TFM mit Hüllkurve der gleichen Querbohrung (rechts). Die Rasterauflösung beträgt 0,16 mm (λ/4,0) bei einer max. Amplitude von 122,6 %.

Die Verwendung solcher oszillatorischen TFM-Bild ist allerdings mit einigen Nachteilen verbunden. Das gilt z. B. für die TFM-Rasterauflösung, da der Abstand zwischen zwei Pixeln im Rahmen ca. λ/8 betragen muss, um normkonform zu sein [1]–[3]. In diesem Artikel entspricht λ der Wellenlänge der Sensormittenfrequenz und der Schallgeschwindigkeit im Prüfteil. Eine geringe Rasterauflösung bedeutet einen großen Berechnungsaufwand, was sofort zu einer niedrigeren Erfassungsrate führt. Ein stabiles Bild mit entsprechender Fehlergrößenbestimmung mit Amplitudenverfahren wird ebenfalls durch ein oszillatorisches TFM-Bild beeinträchtigt. Die max. Amplitude eines gemessenen Echos ist nämlich in erster Linie eine Funktion des Phasen-Offsets des erfassten Signals.

All diese Probleme können mit einem optimierten TFM-Bild mit Signalhüllkurve beseitigt werden, da die Signaloszillationen im Bild entfallen und eine stabile Messung der max. Amplitude ermöglicht (siehe Abbildung 1). Die Erfassungsproduktivität profitiert von der Verwendung der TFM-Signalhüllkurve, da sie bei gleicher Empfindlichkeit gegenüber der Amplitude im Vergleich zum Standard-TFM-Bild eine geringe Rasterauflösung erfordert (d. h. größen Abstand zwischen zwei benachbarten Pixeln). Beispielsweise ist eine Rasterauflösung von ca. λ/4 mit der TFM-Signalhüllkurve ausreichend, um die gleiche Amplitudentreue (2 dB) wie mit dem oszillatorischen TFM-Bild bei einer Auflösung von λ/8 zu erhalten [3].

Das Ziel dieses Artikels ist es, ZfP-Experten über die Vorteile der TFM-Signalhüllkurve zu informieren. Zuerst erfolgt eine Kurzdarstellung des FMC-TFM-Ansatzes und dann eine kurze Präsentation der Konzepte bezüglich der Berechnung der optimierten TFM-Bilder. Am Ende sind die Vorteile der optimierten TFM-Bilder als Teil einer normkonformen Lösung im Vergleich zu oszillatorischen Standard-TFM-Bildern erläutert.

Zusammenfassung des FMC-TFM-Ansatzes

Das Markenzeichen von Ultraschall-Phased-Array ist die Möglichkeit, auf jede gewünschte Stelle im Prüfteil zu fokussieren. Das Phased-Array-Fokussierverfahren verwendet Verzögerungen bei der Übertragung und beim Empfang, um die Laufzeitbeugung von kurzen gesendeten Signalen an der gewünschten Stelle zu synchronisieren. Im Fokusbereich des Prüfteils wird die generierte Gesamtbreite des Schallbündels schmaler und die entsprechende Erkennungsauflösung erhöht sich erheblich [4]–[12].

Die TFM-Funktion ist eine natürliche Erweiterung dieses Ansatzes. Sie generiert mittels Phased-Array-Fokussierung und -Steuerung ein fokussiertes Schallbündel an jeder gewünschten Stelle im Prüfteil und nur der Satz aus hochaufgelösten fokussierten Datenpunkten wird angezeigt [13]–[16]. Häufig besteht der Prüfbereich aus einem einheitlichen kartesischen Raster mit allen gewünschten Fokuszielen. Eine Fokussierung an jeder Rasterposition unter Verwendung von Schallbündeln mit konventionellem Ultraschall mit ihren physikalischen Eigenschaften würde aufgrund der erforderlichen physikalischen Schallausbreitungszeit für jede gewünschte Position äußerst zeitaufwendig sein.

Da konventionelle Ultraschallwellen für ZfP-Anwendungen linear verlaufen, kann die physikalische Schallbündelbildung aufgrund der Überlagerung der aktuellen akustischen Felder für alle beteiligten Elemente einer gegebenen Apertur in einer Nachbearbeitung basierend auf dem FMC-Datensatz nachgebildet werden. Ein Abruf von FMC-Daten setzt eine Signalaufzeichnung von allen Elementen der Empfängerapertur voraus, während eine Schallemission von jedem einzelnen Element mit Sendeapertur erzeugt wird. Als solches wird der FMC-Datensatz durch viele rohe A-Bilder für alle Kombinationen von Sende- und Empfangselementen gebildet.

Wie mit herkömmlicher fokussierter Phased-Array-Technik muss für eine fokussierte Amplitude von einer gegebenen Fokusposition Folgendes erfolgen:

• Berechnung der Laufzeit, die zur Schallausbreitung benötigt wird, um die Fokusstelle zu erreichen, die mit einer ausgewählten Rasterposition übereinstimmt, und zurück zum Empfängerelement aller Sender- und Empfängerelementpaare der Apertur zu gelangen
• Auswahl des Amplitudendatenpunktes entsprechend der geeigneten vollständigen Laufzeit aller Sender- und Empfängerelementpaare der Apertur
• Summe aller ausgewählten Amplitudendatenpunkte von allen Elementen der Sender- und Empfängeraperturen
• Position der summierten Amplitude an der ausgewählten Anfangsposition im Raster

Werden diese Schritte für alle Rasterpositionen des Prüfbereichs wiederholt, wird eine Amplitudenkarte, in der alle Amplitudenwerte beim Senden und Empfangen einem fokussierten Schallbündel entsprechen, erzeugt. Die Verwendung der FMC-Daten zur Erzeugung einer Amplitudenkarte mit den gewünschten Fokusstellen im Prüfbereich (TFM-Bereich) wird als FMC-TFM-Verfahren bezeichnet.

Berechnung der TFM-Signalhüllkurve

In diesem Abschnitt wird die Berechnung der TFM-Hüllkurve mittels roher A-Bilder (FMC), derselben wie für Standard-TFM-Bilder, erläutert. Es ist zu beachten, dass die Hüllkurve eine physikalische Erscheinungsform aufweist und nicht nur ein Bildglättungsalgorithmus ist. Die Hüllkurve des TFM-Bilds besteht aus einzelnen A-Bildern. Um das Verhalten zunächst schematisch darzustellen, wird das Konzept der Hüllkurve anhand einer Gauß-Impulsserie verwendet. Das Verfahren wird auch für ein empirisches A-Bild und ein vollständiges TFM-Bild angewendet.

Das Signal a(t) entspricht dem erfassten Signal (d. h. dem Äquivalent eines mittels FMC erfassten rohen A-Bilds) und ist der Realteil eines komplexen analytischen Signals z(t), das wie folgt beschrieben werden kann:

wobei a’(t) dem imaginären Teil des analytischen Signals und θ(t) der unmittelbaren Signalphase entspricht. Der imaginäre Teil wird effektiv unter Verwendung der Hilbert-Transformation berechnet [17]. Die Signal-Hüllkurve entspricht der Norm eines analytischen Signals, das wie folgt beschrieben werden kann:

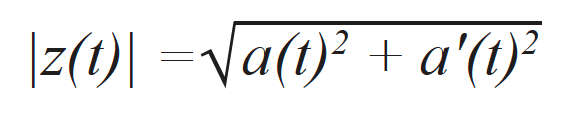
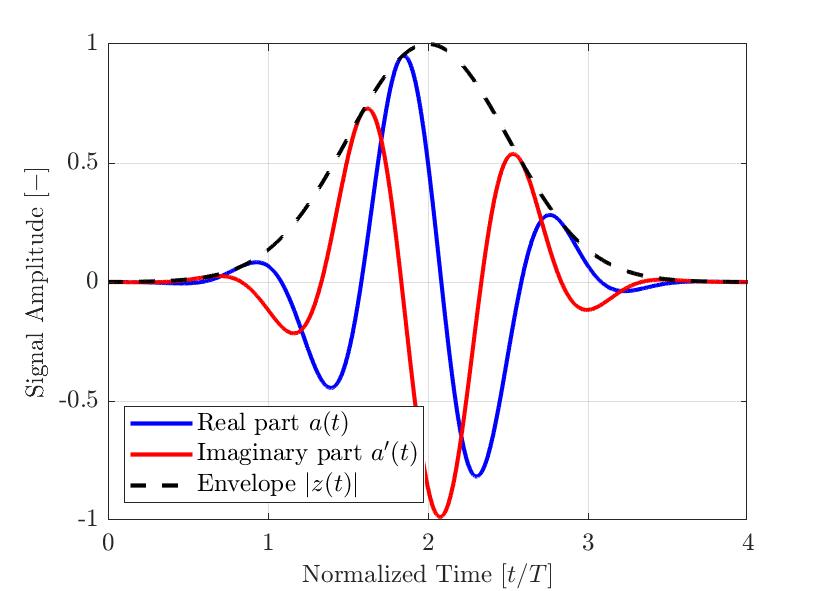
Abbildung 2: Typischer Gauß-modulierter Impuls für ZfP-Anwendungen. Gezeigt sind der reale und der imaginäre Teil sowie die berechnete Hüllkurve. Die Zeit-Achse ist mit der ausgewählten Mittenfrequenzeinheit des Impulses normalisiert.

Abbildung 2 zeigt ein Beispiel eines einfachen Gauß-modulierten Impulses a(t). Der reale Teil des Signals a(t) ist blau dargestellt, der mittels Hilbert-Transformation berechnete imaginäre Teil a’(t) rot und die Hüllkurve |z(t)| las gestrichelte Linie. Wie in der obigen Gleichung zu sehen ist, wird die Signal-Hüllkurve |z(t)| nicht durch die unmittelbare Signalphase θ(t) beeinträchtigt. Daher können Signale mit unterschiedlichen Phasen-Offsets ϕ die gleiche Hüllkurve haben. In Abbildung 3 sind mehrere Gauß-modulierte Impulse mit unterschiedlichen Phasen-Offsets ϕ und ihrer Hüllkurve abgebildet. Daher ist die gemessene max. Signalamplitude bei Verwendung der Signal-Hüllkurve stabiler als der Absolutwert des realen Teils des analytischen Signals.

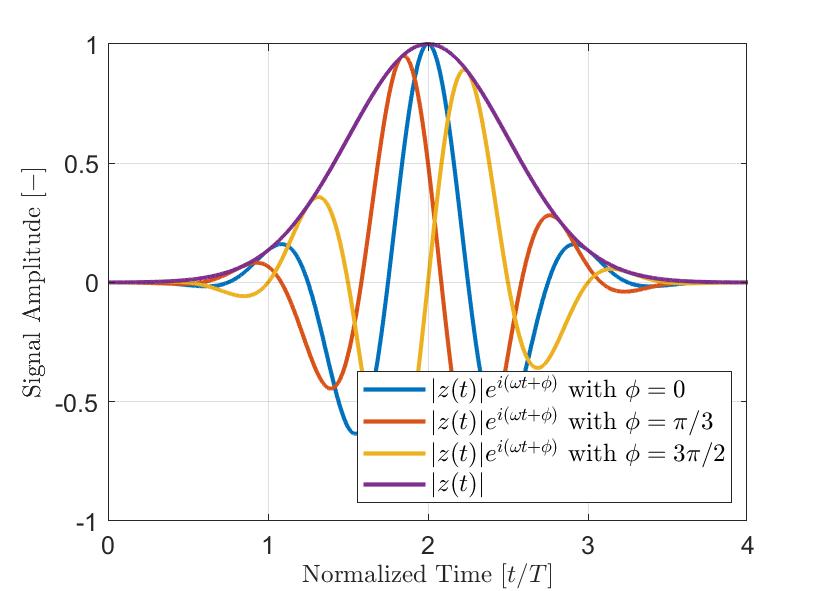
Abbildung 3: Typische Gauß-modulierte Impulse (|z(t)|e^i(ωt+ϕ)) mit verschiedenen Phasen-Offsets ϕ. Die Signal-Hüllkurve |z(t)| ist eindeutig unabhängig von der unmittelbare Phase des analytischen Signals.

Dasselbe Verfahren kann zum Erhalt der Hüllkurve eines empirischen A-Bilds verwendet werden. In Abbildung 4 ist ein typisches mit FMC erfasstes rohes A-Bild gezeigt. In Abbildung 5 ist dasselbe A-Bild (blau) mit der Hilbert-Transformation (rot) und der berechneten Hüllkurve (gestrichelte Linie) dargestellt. Alle abgebildeten Signale sind entsprechend der max. Amplitude der Hüllkurve normalisiert.

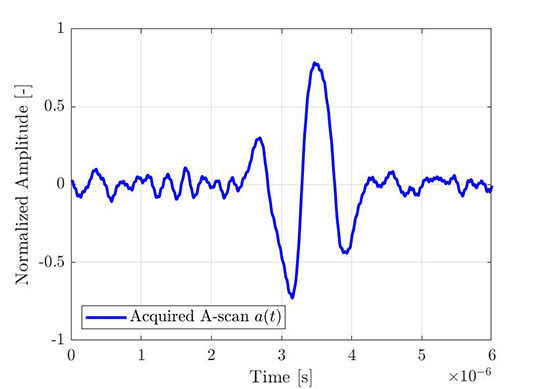Abbildung 4: Anteil eines rohen A-Bilds (erfasst mit FMC).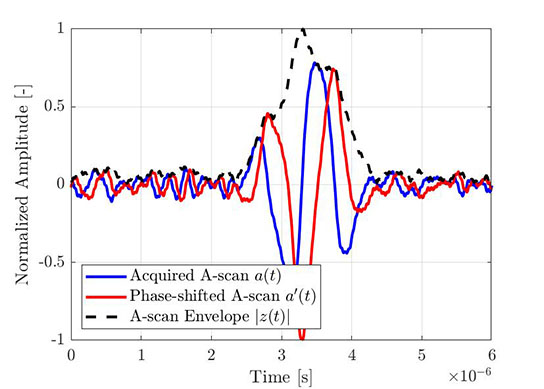

Abbildung 5: Dasselbe A-Bild mit Hilbert-Transformation und berechneter Hüllkurve.

Das Bild der TFM-Hüllkurve (mit einzelnen Rasterpunkten (k,l)), wird unter Verwendung der analytischen Signale von allen A-Bildern berechnet [15]. Sie ist im Grunde das Ergebnis der Berechnung der Norm eines analytischen TFM-Bilds y(k,l), das aus einem Standard-TFM-Rahmen x(k,l), der mit erfassten Standard-FMC-Daten berechnet wurde, und einem TFM-Bild x'(k,l), das mit Hilbert-transformierten FMC-Daten berechnet wurde, zusammengesetzt ist. In beiden Fällen wurden die gleichen Verzögerungssätze verwendet. Die TFM-Hüllkurve wird dann nach folgender Formel berechnet:

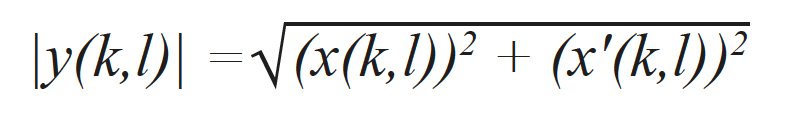
Ein optimiertes TFM-Bild ist daher das Ergebnis einer Kombination aus zwei TFM-Bildern (siehe Abbildung 6): von einem realen Teil der rohen A-Bilder und vom berechneten imaginären Teil der rohen A-Bilder. Während dieses Verfahrens ist der Berechnungsaufwand erhöht und die Erfassungsgeschwindigkeit des Prüfgeräts verringert. Im nächsten Abschnitt wird gezeigt, dass die erforderliche Rasterauflösung erheblich reduziert werden kann, ohne dabei die Amplitudentreue zu beeinträchtigen, und so die Erfassungsgeschwindigkeit auf eine Rate erhöht wird, die höher ist als bei Verwendung des Standard-TFM-Bilds.

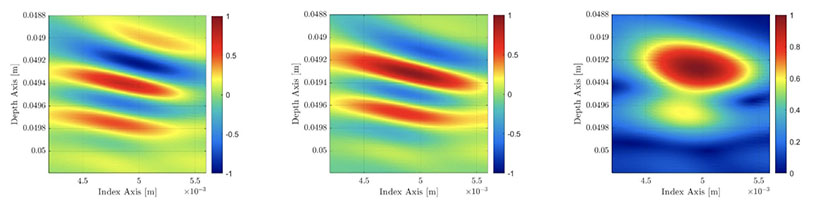
Abbildung 6: Standard-TFM-Bild nicht in absolutem Wert (links). TFM-Bild mit Hilbert-Transformation der FMC (Mitte). TFM-Signalhüllkurve (rechts).

Vorteile der TFM-Signalhüllkurve

In diesem Abschnitt werden die Vorteile der TFM-Hüllkurve anhand eines Vergleichs mehrerer TFM-Bilder mit unterschiedlichen Rasterauflösungsverhältnissen von λ/9,3 bis λ/4,0 und einer Überprüfung verschiedener kritischer Prüfeinheiten dargelegt. Die Ergebnisse wurden unter Verwendung eines 5L32-A31 Sensors und eines SA31-N55S-IHC Vorlaufkeils mit einem Stahlprüfblock mit Querbohrungen mit einem Durchmesser von 1 mm erhalten (siehe Abbildung 7). Ein Ankoppelmittel (Sonotech Ultragel II) wurde zwischen Vorlaufkeil und Stahlprüfblock aufgetragen. Daten wurden mit dem OmniScan X3 Prüfgerät erfasst. Als Schallweg wurde der Impuls-Echo-Modus (T-T) wurde und der Prüfbereich betrug 20 mm × 20 mm. Die Wellenlänge entsprechend des Prüfteils und des Schallweg ist λ = 0,648 mm. Die Rasterauflösung ist als Wellenlängenanteil angegeben.

Abbildung 7: Einstellungen zur Erfassung der TFM-Bilder in Tabelle 1. Das blaue Rechteck entspricht dem gesamten Prüfbereich (20 mm × 20 mm) und das rote Rechteck entspricht dem vergrößerten Prüfbereich (5 mm × 5 mm) [siehe Abbildungen in Tabelle 1]. Es wurde ein 5L32-A31 Sensor und ein SA31-N55S-IHC Vorlaufkeil verwendet. Der Stahlprüfblock hatte eine Dicke von 40 mm.

In Tabelle 1 sind die TFM-Bilder für vier verschiedene Rasterauflösungen von λ/9,3 bis λ/4,0 für das Standard-TFM-Bild und das optimierte TFM-Bild angegeben. Die berechneten Werte der Amplitudentreue [3] und der Erfassungsrate sind in jedem Bild angeben.

Rasterauflösung	Standard-TFM-Bild	Optimiertes TFM-Bild
λ/9,3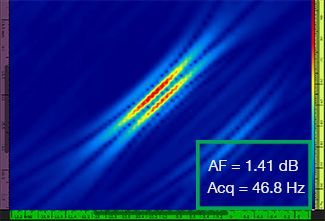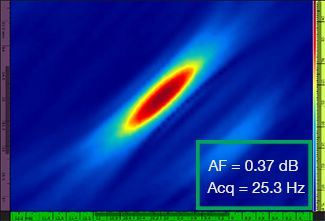
λ/8,1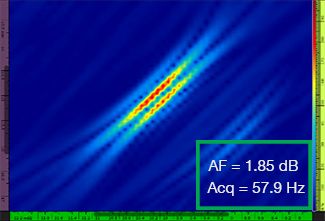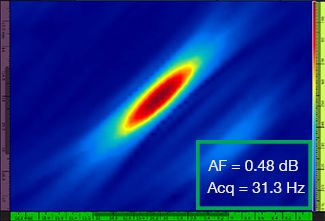
λ/5,9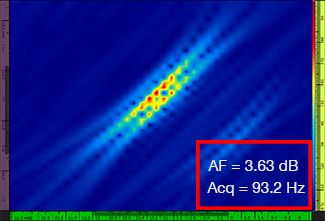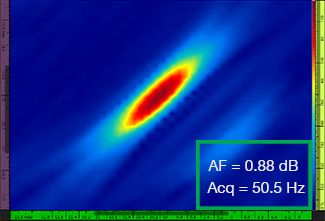
λ/4,0

Erst seit Kurzem ist nach Normen und Standards [1, 2] eine Amplitudentreue von 2 dB oder weniger gültig. Daher sind nur die ersten zwei Werte der Rasterauflösung (λ/9,3, λ/8,1) mit dem Standard-TFM-Bild normkonform. Die TFM-Hüllkurve ermöglicht eine gröbere Rasterauflösung (λ/4,0) unter Beibehaltung einer normkonformen Amplitudentreue. Die Verwendung der TFM-Hüllkurve mit einem gröberen Raster führt zu einer erhöhten Erfassungsgeschwindigkeit von ca. 37 % entsprechend der höchsten Erfassungsrate, die durch das normkonforme Standard-TFM-Bild erreicht wird (57,9 Hz bei λ/8,1).

Zusammenfassung

Die Methode zur Berechnung der Hüllkurve eines TFM-Bilds wurde an einfachen Beispielen dargestellt. Es wurde gezeigt, dass die Signal-Hüllkurve unabhängig von der unmittelbaren Phase ist und somit eine stabilere Grundlage zur Fehlererkennung mit Amplitudenverfahren (wie einem Amplitudenabfall von 6 dB) ermöglicht. Die Signal-Hüllkurve ist mehr als nur eine Bildglättung und sollte nicht als Filter betrachtet werden, der zu Datenverlusten führen kann. Die Vorteile der Hüllkurve bei der TFM-Bildgebung wurden durch Vergleiche von TFM-Bildern mit und ohne Hüllkurve für verschiedene Werte der Rasterauflösung gezeigt. Obwohl zwei TFM-Bilder berechnet werden müssen, um die TFM-Hüllkurve zu erhalten, kann der Verarbeitungsaufwand erheblich reduziert werden, indem eine gröbere normkonforme Rasterauflösung verwendet wird. Dies ist auf die Unempfindlichkeit der Hüllkurve gegenüber der Amplitudenschwankungen zurückzuführen. Das Ergebnis ist ein Bild, das besser an die Amplitudengröße angepasst ist und dennoch schneller erhalten wird als das äquivalente Standard-TFM-Bild.

Literaturnachweis

[1] ASME Committee (2019): ASME BPVC.V Article 4 Mandatory Appendix XI Full Matric Capture. In: ASME.

[2] ASME Committee (2019): ASME BPVC.V Article 4 Nonmandatory Appendix F - Examination of Welds Using Full Matric Capture. In: ASME.

[3] N. Badeau, A. Le Duff und C.-H. Kwan (2020): Theoretical Model for Amplitude Fidelity Reading (submitted). In: ASNT Research Symposium.

[4] A. C. Clay, S.-C. Wooh, L. Azar und J.-Y. Wang (1999): Experimental Study of Phased Array Beam Steering Characteristics. In: Journal of Nondestructive Evaluation, Vol. 18, Nr. 2, S. 13.

[5] L. J. Bond (2018): Fundamentals of Ultrasonic Inspection. In: ASM Handbook, Vol. 17, Nr. Nondestructive Evaluation of Material, S. 155–168.

[6] S.-J. Song, H. J. Shin und Y. H. Jang (Mai 2002): Development of an ultra sonic phased array system for nondestructive tests of nuclear power plant components. In: Nuclear Engineering and Design, Vol. 214, Nr. 1–2, S. 151–161. doi: 10.1016/S0029-5493(02)00024-9.

[7] S. Mahaut, O. Roy, C. Beroni und B. Rotter (Mai 2002): Development of phased array techniques to improve characterization of defect located in a component of complex geometry. In: Ultrasonics, Vol. 40, Nr. 1–8, S. 165–169. doi: 10.1016/S0041-624X(02)00131-2.

[8] S. C. Mondal, P. D. Wilcox und B. W. Drinkwater (August 2005): Design of Two-Dimensional Ultrasonic Phased Array Transducers. In: Journal of Pressure Vessel Technology, Vol. 127, Nr. 3, S. 336–344. doi: 10.1115/1.1991873.

[9] S.-C. Wooh und Y. Shi (April 1998): Influence of phased array element size on beam steering behavior. In: Ultrasonics, Vol. 36, Nr. 6, S. 737–749. doi: 10.1016/S0041-624X(97)00164-9.

[10] Joon-Hyun Lee und Sang-Woo Choi (Mai 2000): A parametric study of ultrasonic beam profiles for a linear phased array transducer. In: IEEE Trans. Ultrason., Ferroelect., Freq. Contr., Vol. 47, Nr. 3, S. 644–650. doi: 10.1109/58.842052.

[11] R. Ahmad, T. Kundu und D. Placko (April 2005): Modeling of phased array transducers. In: The Journal of the Acoustical Society of America, Vol. 117, Nr. 4, S. 1762–1776. doi: 10.1121/1.1835506.

[12] B. W. Drinkwater und P. D. Wilcox (Oktober 2006): Ultrasonic arrays for non-destructive evaluation: A review. In: NDT & E International, Vol. 39, Nr. 7, S. 525–541. doi: 10.1016/j.ndteint.2006.03.006.

[13] P. D. Wilcox (2006): Exploiting the Full Data Set from Ultrasonic Arrays by Post-Processing. In: AIP Conference Proceedings, Brunswick, Maine (USA), Vol. 820, S. 845–852. doi: 10.1063/1.2184614.

[14] J. Zhang, B. W. Drinkwater und P. D. Wilcox (Juli 2011): Effects of array transducer inconsistencies on total focusing method imaging performance. In: NDT & E International, Vol. 44, Nr. 4, S. 361–368. doi: 10.1016/j.ndteint.2011.03.001.

[15] C. Holmes, B. W. Drinkwater und P. D. Wilcox (November 2008): Advanced post-processing for scanned ultrasonic arrays: Application to defect detection and classification in non-destructive evaluation. In: Ultrasonics, Vol. 48, Nr. 6–7, S. 636–642. doi: 10.1016/j.ultras.2008.07.019.

[16] C. Holmes, B. W. Drinkwater und P. D. Wilcox (Dezember 2005): Post-processing of the full matrix of ultrasonic transmit–receive array data for non-destructive evaluation. In: NDT & E International, Vol. 38, Nr. 8, S. 701–711. doi: 10.1016/j.ndteint.2005.04.002.

[17] D. Gabor (1946): Theory of Communication. In: Journal of the Institution of Electrical Engineers, Vol. 96, S. 429–441.