Autoren: Nicolas Badeau, Guillaume Painchaud-April und Chi-Hang Kwan
Zusammenfassung
Die TFM-Prüftechnik (Total Focusing Method) ist nun in Normen und Standards für die zerstörungsfreie Prüfung (ZfP) enthalten, wie z. B. in ASME Section V. Ein wichtiger Parameter, der in diesen Normen und Standards für die TFM-Prüfplanung angegeben ist, ist die Amplitudentreue. Sie ist als die Amplitudenvariation definiert, die für einen bestimmten Reflektor aufgrund der endlichen Auflösung des Abbildungsrasters erhalten wird. Der typische zulässige Grenzwert der Amplitudentreue in diesen Normen und Standards beträgt maximal 2 dB. Während in den Normen und Standards experimentelle Methoden vorgeschlagen werden, um die Amplitudentreue einer bestimmten Konfiguration zu messen, wird in diesem Whitepaper eine einfache und konservative analytische Methode vorgeschlagen. Die Verwendung der TFM-Hüllkurve wird auch bei der Schätzung der Amplitudentreue berücksichtigt, da sie die Verwendung eines weniger dichten TFM-Rasters ermöglicht, ohne dass der Wert der Amplitudentreue den festgelegten Toleranzwert überschreitet. Für die Standard-TFM-Bildgebung zeigten die empirischen Ergebnisse, dass eine Rasterauflösung von etwa λ0/10 erforderlich ist, um eine Amplitudentreue unter 2 dB zu erreichen. Für die TFM-Bildgebung mit Hüllkurve zeigten die empirischen Ergebnisse, dass eine Rasterauflösung von λ0/3,3 erforderlich ist, um dem Standard zu entsprechen.
Einführung
Die Total Focusing Method (TFM) ist eine neu anerkannte Technik für die zerstörungsfreie Prüfung (ZfP) von Komponenten. In manchen Standards und Normen (wie ASME V [1]) wurde FMC (Full Matrix Capture) und TFM als eine zusätzliche Phased-Array-Ultraschallprüftechnik hinzugefügt. Während FMC/TFM in der ZfP-Industrie relativ neu ist, wird es in der Medizin schon seit einiger Zeit als Goldstandard für die medizinische Ultraschallbildverarbeitung eingesetzt [2-4]. Die meisten medizinischen Ultraschallbildgebungstechniken werden in der Regel mit der TFM-Bildgebung verglichen und bewertet.
Es gibt zwar mehrere FMC/TFM-ähnliche Techniken (z. B. VTFM [5], IWEX [6], SAFT [7]), doch der am häufigsten verwendete Algorithmus ist der Verzögerungs- und Summierungsvorgang [2-4,8,9]. Das FMC/TFM-Verfahren besteht aus einem Erfassungsschema (FMC), das auf der Erfassung des Signals aller Kombinationen der Sender- und Empfängerelemente beruht, und einem Summierungsschema (TFM), das das Ergebnis des fokussierten Schallbündels an mehreren Stellen in einem Bereich von Interesse berechnet. Der TFM-Bereich von Interesse ist häufig über ein kartesisches Raster vernetzt. Einzelne Rasterschnittpunkte, an denen die Ultraschall-Fokussierung angewendet wird, werden als Pixel bezeichnet. Das Fokussierungsverfahren ähnelt der Standard-Phased-Array-Ultraschallbildgebung, mit dem Unterschied, dass die Schallbündel in der Nachverarbeitung unter Verwendung der gespeicherten Daten in der FMC-Datenmatrix gebildet werden. Der Verzögerungs- und Summierungsvorgang nach der Erfassung geht von der Linearität der zugrundeliegenden Schallwellen aus, wie sie in typischen ZfP-Anwendungen zu finden sind.
Die FMC/TFM-Technik kann als natürliche Erweiterung der herkömmlichen Phased-Array-Technik betrachtet werden. Aufgrund der Unterschiede in der Datendarstellung im Vergleich zur herkömmlichen Phased-Array-Ultraschallprüfung (PAUT) müssen jedoch neue Konfigurationsparameter berücksichtigt werden. Ein solches Konzept ist die Amplitudentreue eines TFM-Rasters. Die Amplitudentreue ist als die maximale Amplitudenvariation einer Anzeige definiert, die durch die TFM-Rasterauflösung {Δx,Δz} verursacht wird. Die Verwendung eines einheitlichen kartesischen Koordinatensystems, d. h. (Δx=Δz), wird für den Rest dieser Studie berücksichtigt. Die Amplitudentreue kann als Gleichung wie folgt ausgedrückt werden:
![(Gl. 1) AF(Δx)≡-20 log〖(A_(sampled max) (Δx))/A_(true max) 〗 [dB], wobei:](https://industrial.evidentscientific.com.cn/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_01.jpg?rev=43A1)
sampled max die gemessene maximale Amplitude eines Merkmals von Interesse basierend auf einer begrenzten Rasterabtastung ist, und Atrue max das Maximum desselben Merkmals von Interesse basierend auf einer unbegrenzten Rasterauflösung ist. Der Grenzwert, bei dem die Rastergröße über die beiden Achsen für Asampled max (Δx) Null wird, definiert Atrue max, und die entsprechende Amplitudentreue wird 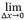 AF(Δx)=0. Gleichung 1 liefert eine formale Definition zur Berechnung der Amplitudentreue in Bezug auf die Rasterauflösung. In der Praxis kann jedoch das wahre Maximum Atrue max des zugrundeliegenden Signals nur durch Oversampling des TFM-Amplitudenbildes und Interpolation geschätzt werden,
AF(Δx)=0. Gleichung 1 liefert eine formale Definition zur Berechnung der Amplitudentreue in Bezug auf die Rasterauflösung. In der Praxis kann jedoch das wahre Maximum Atrue max des zugrundeliegenden Signals nur durch Oversampling des TFM-Amplitudenbildes und Interpolation geschätzt werden,
![(Gl. 2) (AF) ̂(Δx)=-20 log〖(A_(sampled max) (Δx))/A ̂_(true max) 〗 [dB], wobei:](https://industrial.evidentscientific.com.cn/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_02.jpg?rev=43A1)
 true max ist ein geschätzter Wert von Atrue max. ist.
true max ist ein geschätzter Wert von Atrue max. ist.
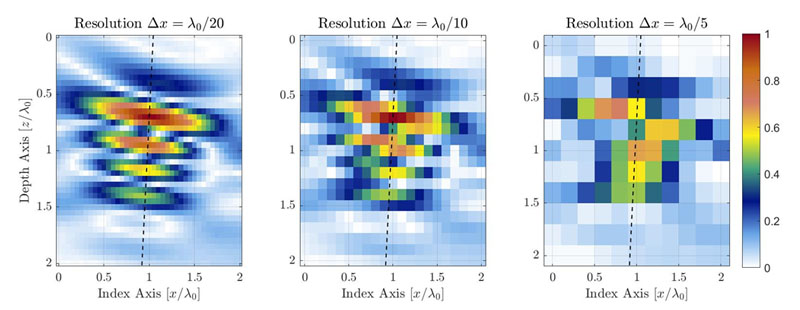
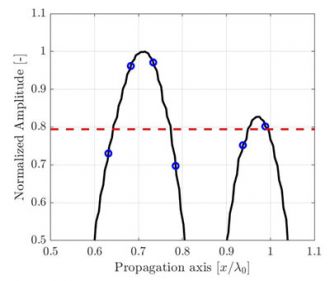
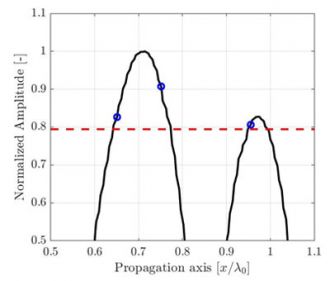
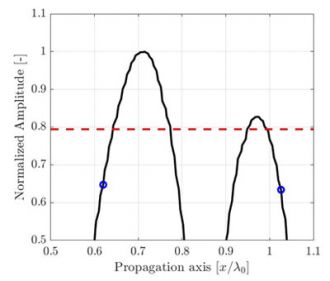
Abbildung 1: Verschlechterung der TFM-Bildqualität, verursacht durch eine abnehmende TFM-Rasterauflösung. Die gestrichelten Linien repräsentieren die Hauptachse der Schallausbreitung.
Für einen identischen Bereich von Interesse hat eine gröbere Rasterauflösung eine niedrigere Pixelanzahl. Abbildung 1 zeigt typische TFM-Bilder derselben Querbohrung für verschiedene Rasterauflösungswerte. Die Rasterauflösung ist als ein Bruchteil der Wellenlänge der Sensorzentralfrequenz λ0= c/f0 definiert, wobei die Schallgeschwindigkeit im Prüfteil und f0 die Sensorzentralfrequenz ist.
In Normen und Standards wird inzwischen eine Amplitudentreue von maximal 2 dB gefordert [1,10]. Diese Anforderung ergibt sich aus dem anwendungsspezifischen Kompromiss zwischen einer ausreichenden Bildqualität, um eine ordnungsgemäße ZfP-Analyse zu gewährleisten, und der Prüfproduktivität, die stark von der Dichte des TFM-Rasters eines bestimmten Bereichs von Interesse beeinträchtigt wird. Es ist zu beachten, dass das Gleichgewicht zwischen TFM-Bildqualität und Prüfproduktivität besonders kritisch für autonome tragbare Geräte ist, die keinen Zugang zu einer großen Rechenleistung haben. Es wird erwartet, dass dieses Problem im Laufe der Zeit nicht mehr existiert, wenn sich die Energieeffizienz der eingebetteten Hardware verbessert und Remote-Berechnungen größtenteils verfügbar werden.
Obwohl einige empirische Methoden vorgeschlagen wurden [10–12], erfordern sie normalerweise umfangreiche Berechnungen, und die erhaltenen Ergebnisse sind nicht repräsentativ für die wahre Amplitude, die durch die Rasterauflösung verursacht wird, was ein Problem ist, das im folgenden Abschnitt erläutert wird. Dieses Whitepaper stellt eine Methode zur genauen Schätzung der Amplitudentreue einer TFM-Konfiguration vor, um Prüfer der zerstörungsfreien Prüfung bei der Durchführung einer normkonformen und produktiven TFM-Prüfung zu unterstützen.
Das Whitepaper ist wie folgt gegliedert. Zuerst wird die Problemstellung umfassend erläutert, mit der ZfP-Prüfer konfrontiert sind. Anschließend wird ein Verfahren zur empirischen Messung der Amplitudentreue einer TFM-Konfiguration beschrieben. Im folgenden Abschnitt wird ein analytisches Modell zur Schätzung der Amplitudentreue vorgeschlagen. Das vorgeschlagene Modell wird dann mit empirischen Messungen anhand drei verschiedener TFM-Anwendungen verglichen. Abschließend folgt eine kurze Zusammenfassung der Arbeit.
Problemstellung
Während ein sehr feines (d. h. dichtes) Raster eine sehr kleine Amplitudentreue ermöglicht, haben moderne elektronische Geräte, die Live-TFM-Bilder berechnen können, immer noch rechnerische Grenzen. Eine feinere Rasterauflösung über einen bestimmten Bereich von Interesse bedeutet, dass eine große Anzahl Fokussierungspunkte zu berechnen ist, was zu einer Verringerung der Prüfproduktivität und der mechanischen Abtastgeschwindigkeit führt. Der ZfP-Prüfer muss eine geeignete Rasterauflösung auswählen können, die die Prüfproduktivität maximiert und gleichzeitig die Normkonformität gewährleistet.
Die Amplitudentreue lässt sich anhand einer einfachen eindimensionalen Signalprobe an verschiedenen Perioden veranschaulichen. In dem in Abbildung 2 dargestellten Beispiel ist das eindimensionale Signal die Amplitude der in Abbildung 1 dargestellten Querbohrung entlang der akustischen Ausbreitungsachse von einem hochauflösenden λ0/100-Bild. Für das Beispiel wird nur ein vergrößerter Ausschnitt nahe der maximalen Signalamplitude dargestellt. Erneut sind die Messungen bei drei verschiedenen Auflösungen λ0/20, λ0/10 und λ0/5 durch blaue Kreise über einer hochauflösenden, interpolierten Referenz (einfache schwarze Kurve) gekennzeichnet.
(a) Die Auflösung des diskreten Rasters beträgt λ0/20, und die berechnete Amplitudentreue beträgt AF = 0,27 dB. |
(b) Die Auflösung des diskreten Rasters beträgt λ0/10, und die berechnete Amplitudentreue beträgt AF = 0,82 dB. |
(c) Die Auflösung des diskreten Rasters beträgt λ0/5, und die berechnete Amplitudentreue beträgt AF = 3,7 dB. |
Abbildung 2: Veranschaulichung der Auswirkung der Abtastperiode auf die aufgezeichnete Amplitude entlang der in Abbildung 1 dargestellten Ausbreitungsachse. Eine hochauflösende interpolierte Signalreferenz (schwarze Linie) ist als Sehhilfe dargestellt. Die normkonforme Amplitudentreue von 2 dB wird durch eine rote gestrichelte Linie dargestellt.
Die offensichtliche Schlussfolgerung ist, dass ein dichteres Raster eine bessere Darstellung eines kontinuierlichen Signals liefert, wie es durch den AF-Wert aus Gleichung 1 quantifiziert wird, aber das Optimierungsproblem bleibt bestehen: Welches die maximale Gittergröße (Δxmax ) ist, die für alle möglichen Rasterpositionen in einem TFM-Bild eine Amplitudentreue  garantiert, die gleich einem Sollwert der AFtarget ist? Oder,
garantiert, die gleich einem Sollwert der AFtarget ist? Oder,
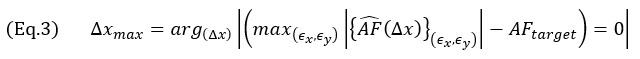
Aus dieser Problemstellung geht hervor, dass alle Translationen des Rasters, die durch Verschiebungen (ϵx,ϵy) gekennzeichnet sind, berücksichtigt werden müssen, um das Maximum  für eine feste Zellengröße (Δx) zu erhalten. Dies dient dazu, alle möglichen Fälle von Rasteranordnungen zur Berechnung des TFM-Bildes abzudecken.
für eine feste Zellengröße (Δx) zu erhalten. Dies dient dazu, alle möglichen Fälle von Rasteranordnungen zur Berechnung des TFM-Bildes abzudecken.
Im folgenden Abschnitt wird das Messprinzip für die Werte der Amplitudentreue veranschaulicht, das sich aus mehreren Rasterverschiebungen { (Δx)}(ϵx,ϵy) ergibt.
(Δx)}(ϵx,ϵy) ergibt.
Empirische Messung der Amplitudentreue
Bevor dargestellt wird, wie die Amplitudentreue mit Hilfe eines einfachen analytischen Modells geschätzt werden kann, ist es von entscheidender Bedeutung zu definieren, wie sie im Falle eines TFM-Bildes experimentell gemessen werden kann. In der ZfP-Industrie wurden bereits mehrere Verfahren beschrieben und vorgeschlagen [10-12], aber einige von ihnen quantifizieren die Amplitudentreue nicht in vollständiger Weise. Die empirische Messung der Amplitudentreue kann für den ZfP-Prüfer schnell zu einer Last werden, da sie die Berechnung vieler TFM-Bilder aus mehreren präzisen TFM-Rasterpositionen erfordert.
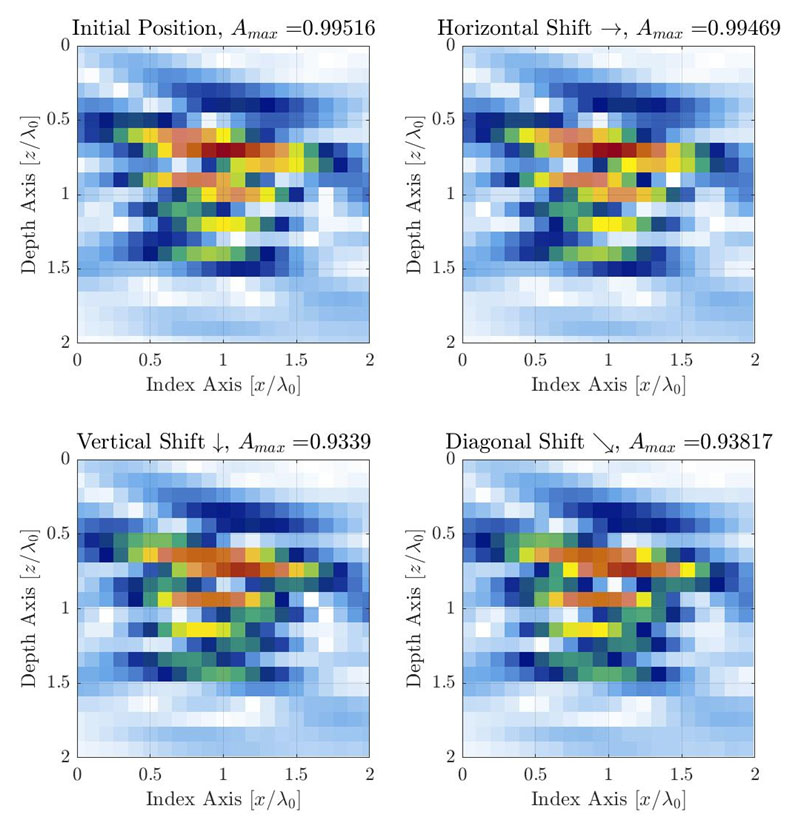
Abbildung 3: Veranschaulichung der Amplitudentreuevariation, die durch die diskrete Rasterauflösung verursacht wird, wenn das Raster in 3 verschiedene Richtungen verschoben wird. Die Rasterauflösung wird auf Δx=Δy=λ0/10 eingestellt. Das Raster wird um ein Viertel der Rasterzelle nach rechts (ϵx=λ0/40,ϵy=0) (oben rechts), nach unten (ϵx=0, ϵy=λ0/40) (unten links) und diagonal (ϵx=λ0/40,ϵy=λ0/40) (unten rechts) verschoben.
Für typische TFM-Anwendungen wird eine Querbohrung als Referenzfehler für die Amplitudenkalibrierung und Messung der Amplitudentreue verwendet [1,10]. Die beobachtete Amplitude variiert am stärksten entlang der Hauptachse der Schallausbreitung, die eine Funktion der Position des Sensors, des Vorlaufkeils und des Prüfbereichs ist (d. h. der TFM-Rasterposition relativ zum Sensor). In dem in Abbildung 1 dargestellten Fall ist die Hauptausbreitungsachse nahezu vertikal. Bei einem allgemeinen Messverfahren ist die Ausbreitungsachse jedoch je nach Messort im Prüfbereich unterschiedlich. Bei einem TFM-Bild muss das Abtastraster in alle Richtungen verschoben werden, um die tatsächliche Amplitudenvariation zu erfassen, die durch das diskrete Raster verursacht wird. Dieser Prozess wird im Folgenden anhand des gleichen Beispiels aus Abbildung 1 (Mitte) mit einer Rasterauflösung von λ0/10 veranschaulicht.
Es wird vorgeschlagen, das Raster um einen Bruchteil der zu prüfenden Rasterauflösung (z. B. etwa ein Zwanzigstel der Auflösung) in jede Richtung zu verschieben, und zwar so oft, wie es nötig ist, um eine Rasterüberlappung zu erhalten. Dies bedeutet, dass zur Abdeckung eines Versatzes einer Rasterauflösung in den beiden orthogonalen Richtungen insgesamt 202 = 400 Verschiebungsschritte erforderlich sind (bei Verwendung des vorgeschlagenen Rasterschrittes von einem Zwanzigstel der Auflösung). Die maximale Amplitude wird für jeden Rasterversatz aufgezeichnet, und die aufgezeichneten Maximal- und Minimalwerte werden verwendet, um die Amplitudentreue unter Verwendung von Gleichung 2 zu erhalten. In dem in Abbildung 3 dargestellten Fall beträgt die Rasterauflösung λ0/10, und die gemessene Amplitudentreue beträgt 0,88 dB. Gemessen an der Anzahl erforderlicher Verschiebungen wäre dieser manuelle Vorgang für den ZfP-Prüfer umständlich und zeitaufwändig. Dies bedeutet auch, dass insgesamt 400 TFM-Bilder berechnet werden müssen, um die Amplitudentreue einer einzelnen Rasterauflösung zu messen.
Erwähnenswert ist, dass durch die Verwendung der Software-Verschiebung der TFM-Rasterposition relativ zum Sensor anstelle einer mechanischen Verschiebung des Sensors relativ zum Prüfteil, nach ASME Section V [12], mehrere TFM-Bilder mit einem einzigen FMC-Datensatz erzeugt werden können. Ein weiterer Vorteil dieses Ansatzes ist die Möglichkeit, auf die vertikale Komponente des Rasters zuzugreifen. Tatsächlich können der Sensor und Vorlaufkeil relativ zur ausgewählten Querbohrung entlang der Tiefenachse nicht mechanisch bewegt werden.
Einige ZfP-Geräte bieten teilautomatisierte Werkzeuge, mit denen das TFM-Raster verschoben, die maximale Amplitude im Prüfbereich aufgezeichnet und schließlich die resultierende Amplitudentreue berechnet werden kann [11]. Doch leider verschieben diese Werkzeuge das Raster meist nur in horizontaler Richtung und unterschätzen damit die Amplitudentreue. Zum Vergleich: Wird das Raster nur entlang der horizontalen Achse verschoben, wie in Abbildung 3 dargestellt, beträgt die gemessene Amplitudentreue 0,06 dB, was mehr 15 Mal niedriger ist als die Amplitudentreue, die bei Berücksichtigung der vertikalen Achse gemessen wird.
Ein phänomenologisches Ansatz zur Schätzung der Amplitudentreue
In diesem Abschnitt wird ein einfaches analytisches Modell vorgeschlagen, das auf empirischen Beobachtungen basiert. Bei diesem phänomenologischen Ansatz wird das Signalverhalten entlang der Hauptausbreitungsachse berücksichtigt, von der angenommen wird, dass sie die meisten Amplitudenschwankungen enthält und daher am empfindlichsten für die Rasterauflösung ist. Abbildung 4 zeigt das empirische Profil eines resultierenden TFM-Bildes einer Querbohrung entlang der Hauptausbreitungsachse (blau) und entlang der Schallbündelmittelachse (rot). Der Ausgangspunkt der Achse befindet sich an der scheinbaren Stelle der maximalen Amplitude der Hüllkurvendarstellung, was den kleinen Versatz entlang der Achse  für die Schwingungsdarstellung erklärt. Die Profile für das oszillatorische Standard-TFM-Bild und für die TFM-Hüllkurve werden bereitgestellt.
für die Schwingungsdarstellung erklärt. Die Profile für das oszillatorische Standard-TFM-Bild und für die TFM-Hüllkurve werden bereitgestellt.
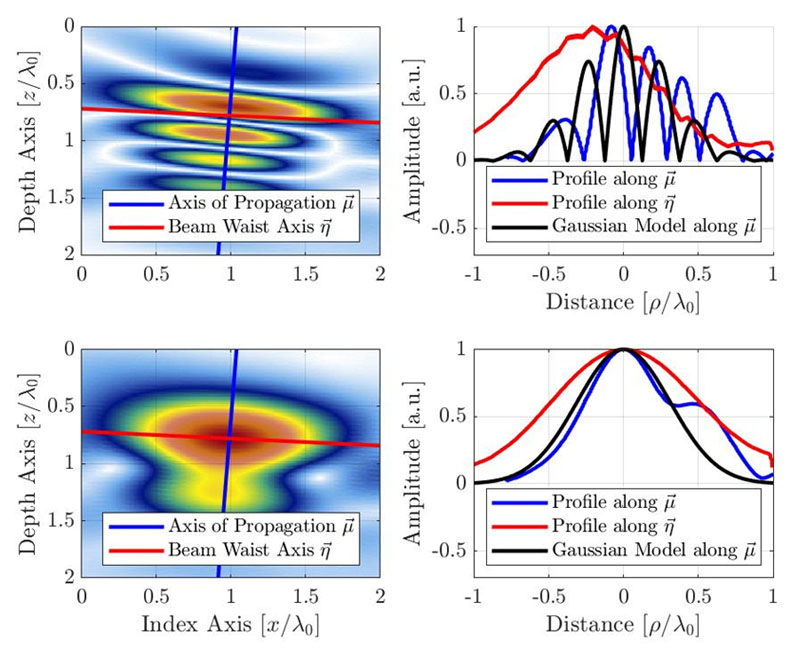
Abbildung 4: TFM-Bild (oben: oszillatorisch, unten: Hüllkurve) mit dem Signalprofil entlang der Schallausbreitungsachse und der Mittelachse des Schallbündels. Das vorgeschlagene Gauß-Modell ist auch für das oszillatorische TFM-Bild und die TFM-Hüllkurve dargestellt. Beachten Sie, dass sich die scheinbare Wellenlänge aufgrund des Impuls-Echoverfahrens der TFM-Schallbündelbildung halbiert.
Wie bereits erwähnt, wird davon ausgegangen, dass die Achse der größten Amplitudenvariation entlang der Hauptachse der Schallausbreitung liegt. Daher zielt das Modell darauf ab, die Amplitudenvariation in dieser Richtung zu reproduzieren. Das Modellsignal ist ein kosinusmoduliertes Gauß-Signal
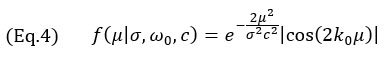
wobei: k0=ω0/c die Wellenzahl bei der zentralen Kreisfrequenz ω0 des Sensors ist, σ der von der zentralen Frequenz abhängige Breitenparameter ist und die relative Bandbreite bw ist. Der Breitenparameter σ wird so berechnet:
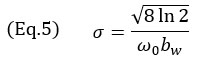
Bei einem typischen Phased-Array-Sensor für die zerstörungsfreie Prüfung liegt die relative Bandbreite nahe der 60 % Grenze, daher wird ein Wert von (bw=0,6) in diesem Modell verwendet. Dies wiederum macht die Hüllkurve nach Gauß größer als eine einzelne Kosinusschwingung. Erwähnenswert ist, dass die Mittenfrequenz des Kosinusterms in Gleichung 3 doppelt so hoch ist, wie die Mittenfrequenz des Sensors. Dies ist auf den Impuls-Echo-Modus in der TFM-Abbildung (Sende- und Empfangsschallweg) zurückzuführen und lässt sich an den Abständen zwischen den Schwingungen in Abbildung 4 ablesen. Tatsächlich wird die Umwandlung zwischen dem Zeitbereich und dem Raumbereich als μ = tc/2 geschrieben. Es erklärt auch den Faktor 2, der als Exponentialterm aus Gleichung 3 verwendet wird.
Da die Hüllkurve nach Gauß viel größer als eine einzelne Schwingung der Kosinusfunktion ist, werden für das Schwingungsmodell aus Gleichung 4 nur die Werte |μ|≤λ0/8 berücksichtigt, da größere Werte räumliches Aliasing für die Amplitudentreue erzeugen.
Für das TFM-Hüllkurvenmodell wird nur der Gauß-Term aus Gleichung 4 verwendet:
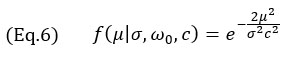
was für alle Rasterauflösungen gilt. Das Profil, das mit dem Modell der Gleichungen 3 und 7 erhalten wurde, ist in Abbildung 4 neben den experimentellen Profilen dargestellt. Es ist zu beachten, dass die empirischen Messungen auch zeigen, dass das Oberflächenwellensignal (das "Wrap-around"-Echo, typisch für Querbohrungen) hinter dem Hauptecho bleibt, ein Merkmal, das in dem vorgeschlagenen Modell nicht vorkommt.
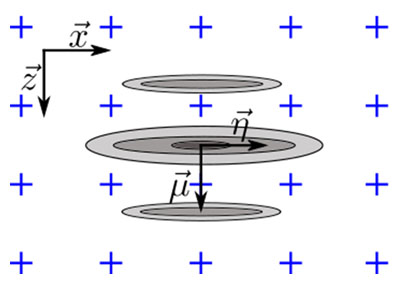
Die Orientierung des Fehlers relativ zu den orthogonalen Achsen des Rasters muss berücksichtigt werden, um mit dem Modell das Worst-Case-Szenario der Amplitudentreue zu erhalten. Wie in Abbildung 5a dargestellt, tritt das Worst-Case-Szenario für das oszillatorische TFM-Bild auf, wenn die Hauptachse der Schallausbreitung  parallel zu einer der Rasterachsen ist. Daher muss die Amplitudentreue so berechnet werden, als ob die maximale Amplitude zwischen zwei Rasterpunkten entlang einer der Achsen
parallel zu einer der Rasterachsen ist. Daher muss die Amplitudentreue so berechnet werden, als ob die maximale Amplitude zwischen zwei Rasterpunkten entlang einer der Achsen 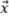 oder
oder 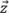 zentriert ist, was folgendes ergibt:
zentriert ist, was folgendes ergibt:
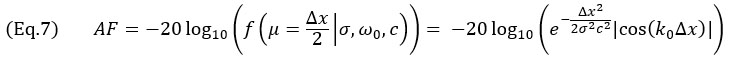
für Δx≤λ0/4. Für die TFM-Hüllkurve tritt das Worst-Case-Szenario ein, wenn das Amplitudenprofil entlang der Hauptausbreitungsachse  und der Tiefenachse der Schallbündel identisch ist.
und der Tiefenachse der Schallbündel identisch ist.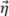 Dieser Fall (siehe Abbildung 5b) entspricht der Darstellung der Querbohrung als Kreis und kann damit als Hauptausbreitungsachse
Dieser Fall (siehe Abbildung 5b) entspricht der Darstellung der Querbohrung als Kreis und kann damit als Hauptausbreitungsachse  jede Ausrichtung haben. Das Worst-Case-Szenario tritt ein, wenn das Echo der Querbohrung, wie dargestellt, zwischen vier benachbarten Punkten zentriert ist. In diesem Fall muss die Amplitudentreue entlang der Rasterdiagonale berechnet werden, was zu folgendem Ergebnis führt:
jede Ausrichtung haben. Das Worst-Case-Szenario tritt ein, wenn das Echo der Querbohrung, wie dargestellt, zwischen vier benachbarten Punkten zentriert ist. In diesem Fall muss die Amplitudentreue entlang der Rasterdiagonale berechnet werden, was zu folgendem Ergebnis führt:
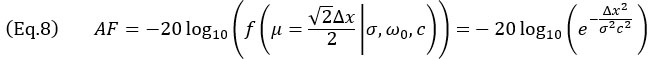
Eine Näherungsform für den Wert von Δx bezüglich der Amplitudentreue in Fällen, in denen der Wert der Amplitudentreue klein ist, was der typische Anwendungsfall für ZfP-Anwendungen ist, kann für das oszillatorische Modell mit Gleichung 7

und für das Hüllkurvenmodell mit der Gleichung 8
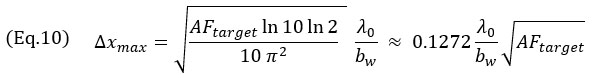
Diese Terme übersetzen in allen Fällen die Quadratwurzelabhängigkeit der Rastergröße in den Wert der Amplitudentreue. Gleichung 9 wurde unter Verwendung der Taylor-Approximation zweiter Ordnung von Gleichung 7 erhalten. Diese Annäherung ist in Abbildung 6 neben dem exakten Modell dargestellt. Beachten Sie auch, dass die Rastergröße des oszillatorischen Modells fast unabhängig von der relativen Bandbreite für kleine b w ist. Erwähnenswert ist auch, dass für das oszillatorische Modell und für das Hüllkurvenmodell die maximale Rasterauflösung Δxmax mit der Quadratwurzel der angestrebten Amplitudentreue zusammenhängt. Diese Werte stellen die maximale Rasterauflösung für das normkonforme phänomenologische Modell dar.
(a) Worst-Case-Szenario für das oszillatorische TFM-Bild tritt auf, wenn Achse |
(b) Worst-Case-Szenario für die TFM-Hüllkurve tritt auf, wenn das Amplitudenprofil entlang |
Abbildung 5: Darstellung der Fehlerausrichtung relativ zur orthogonalen Achse des Rasters für das Worst-Case-Szenario, für (a) das oszillatorische TFM-Bild und (b) die TFM-Hüllkurve.
Validierung der Versuchsanordnung
Das vorgeschlagene Modell wird mit den empirischen Ergebnissen anhand drei verschiedener TFM-Prüfanwendungen validiert. Für alle drei TFM-Konfigurationen wurden mehrere Querbohrungen mit verschiedenen Rasterauflösungen abgebildet. Die Amplitudentreue wurde mit der zuvor beschriebenen Methode gemessen. Die Parameter der drei Anwendungsfälle sind in Tabelle 1 beschrieben. Die erste Anwendung ist in Kontakt mit einem hochfrequenten Sensor (7,5 MHz), die zweite Anwendung verwendet Transversalwellen mit einer niedrigeren Frequenz (5 MHz) und die dritte Anwendung verwendet Transversalwellen mit einer höheren Sensorfrequenz (10 MHz) und Elementanzahl. In allen Fällen befinden sich die Querbohrungen innerhalb von 50 mm von der oberen Oberfläche eines Kohlenstoffstahlblocks.
Tabelle 1: Parameter der TFM-Konfigurationen, die für die Validierung der Versuchsanordnung der Amplitudentreue verwendet wurden.
| Gehäuse | Sensorparameter | Vorlaufkeilparameter | Prüfteilparameter | TFM-Modus | |||||
|---|---|---|---|---|---|---|---|---|---|
|
Frequenz
[MHz] |
Anzahl
[#] |
Abstand
[mm] |
Schallgeschwindigkeit
[m/s] |
Winkel
[°] |
Höhe
[mm] |
Schallgeschwindigkeit
cp - cs [m/s] |
Querbohrung
Diameter [mm] | ||
| 1 | 7,5 | 64 | 1,0 | - | - | 0 | 3240 - 5890 | 1 | L-L |
| 2 | 5 | 32 | 1,0 | 2330 | 36,1 | 11,0 | 3240 - 5890 | 0,5 | T-T |
| 3 | 10 | 64 | 0,5 | 2330 | 36,1 | 11,0 | 3240 - 5890 | 1 | T-T |
Abbildung 5 zeigt die resultierende Amplitudentreue für das oszillatorische Standard-TFM-Bild (oben) und für die TFM-Hüllkurve (unten). Jeder einzelne graue Punkt repräsentiert eine andere Kombination aus Anwendung, Querbohrungen und Rasterauflösung. Die Amplitudentreue, die mit dem zuvor vorgestellten Gauß-Modell geschätzt wurde, ist mit einer schwarzen Kurve dargestellt. Die rote gestrichelte Linie stellt die normkonforme Grenze bei 2 dB dar.
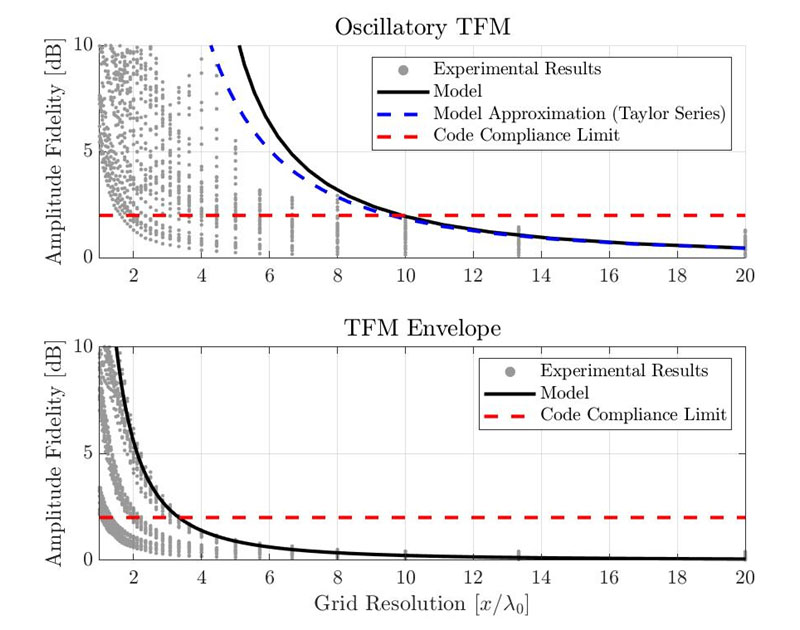
Abbildung 6: Empirische Messungen der Amplitudentreue und Ergebnisse unter Verwendung des vorgeschlagenen Gauß-Modells für die oszillatorische Standard-TFM (oben) und für die TFM-Hüllkurve (unten) im Vergleich.
Mit dem vorgeschlagenen Modell beträgt die erforderliche Auflösung, um dem Standard zu entsprechen, λ0/9,9 für die oszillatorische TFM und λ0/3,3 für die TFM-Hüllkurve. Experimentelle Ergebnisse zeigen, dass die minimale Rasterauflösung für die Normkonformität bei etwa λ0/10 für die oszillatorische Standard-TFM und λ0/3,3 für die TFM-Hüllkurve liegt. Es ist jedoch zu beachten, dass diese Werte aus dem Worst-Case-Szenario des Falls stammen. Einige der gemessenen Werte der Amplitudentreue liegen unter 2 dB, selbst bei einer gröberen Rasterauflösung. Daher ermöglicht das vorgestellte Modell gute, aber dennoch konservative Schätzungen für die Amplitudentreue einer TFM-Konfiguration.
Schlussfolgerung
Die Amplitudentreue einer TFM-Konfiguration ist ein wichtiges Maß für die Bildverarbeitungsrobustheit bezüglich der Rasterauflösung. Umso dichter das Raster ist, desto geringer ist der Wert für die Amplitudentreue. In Normen und Standards ist nun die Total Focusing Method als neue Prüftechnik mit einer reglementierten Amplitudentreue von 2 dB oder weniger enthalten. In diesem Whitepaper wird beschrieben, wie die Amplitudentreue empirisch korrekt gemessen werden kann und wie ein einfaches analytisches Modell verwendet werden kann, um die Amplitudentreue der Ergebnisse einer TFM-Konfiguration zu schätzen.
Es wurde ein einfaches analytisches Modell vorgeschlagen, das auf dem Amplitudenprofil entlang der Hauptachse der Schallausbreitung basiert. Nach dem Modell soll das Amplitudenprofil eine modulierte Kosinusschwingung nach Gauß sein. Die Verwendung dieses Profils zur Schätzung der Amplitudentreue führt zu guten Ergebnissen hinsichtlich des oszillatorischen Standard-TFM-Bilds und der TFM-Hüllkurve. Empirische Ergebnisse zeigten die Notwendigkeit einer Rasterauflösung von bis zu λ0/10 oder λ0/3,3 für das oszillatorische Standard-TFM-Bild und die TFM-Hüllkurve. Das vorgeschlagene analytische Modell schätzt die Notwendigkeit einer Rasterauflösung auf λ0/9,9 für das Standard-TFM-Bild und auf λ0/3,3 für die TFM-Hüllkurve. Das vorgeschlagene Modell könnte daher verwendet werden, um die Amplitudentreue der TFM-Konfiguration einzuschätzen.
Erfahren Sie mehr über die Vorteile der Verwendung der TFM-Hüllkurve als Teil einer normkonformen Lösung im folgenden Whitepaper: Use of the Total Focusing Method with the Envelope Feature.
Literaturverzeichnis
[1] ASME Committee (2019): ASME BPVC.V Article 2019 Mandatory Appendix XI Full Matric Capture.
[2] O. Oralkan, A. S. Ergun, J. A. Johnson, M. Karaman, U. Demirci, K. Kaviani, T. H. Lee, und N. T. Khuri-Yakub (2002): „Capacitive Micromachined Ultrasonic Transducers: Next-Generation Arrays for Acoustic Imaging?,” In: IEEE Trans. Ultrason., Ferroelect., Freq. Contr., 49(11), S. 1596–1610.
[3] K. E. Thomas (1996): „Evolution of Ultrasound Beamformers,” In: IEEE Ultrasonics Symposium. Proceedings, IEEE, San Antonio, TX, USA, S. 1615–1622.
[4] S. Freimann, P. Li, und M. O’Donnell: „Retrospective Dynamic Transmit Focusing,“ S. 24.
[5] P. D. Wilcox (2006): „Exploiting the Full Data Set from Ultrasonic Arrays by Post-Processing,“ AIP Conference Proceedings, AIP, Brunswick, Maine (USA), S. 845–852.
[6] N. Portzgen, D. Gisolf, und G. Blacquiere (2007): „Inverse Wave Field Extrapolation: A Different NDI Approach to Imaging Defects,“ In: IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 54(1), S. 118–127.
[7] R. S. Sharpe, Hrsg. (1982): Research Techniques in Nondestructive Testing. Ausgabe 6: ..., Acad. Press, London.
[8] C. Holmes, B. W. Trinkwasser, und P. D. Wilcox (2008): „Advanced Post-Processing for Scanned Ultrasonic Arrays: Application to Defect Detection and Classification in Non-Destructive Evaluation,“ In: Ultrasonics, 48(6–7), S. 636–642.
[9] C. Holmes, B. W. Trinkwasser, und P. D. Wilcox (2005): „Post-Processing of the Full Matrix of Ultrasonic Transmit-Receive Array Data for Non-Destructive Evaluation“. In: NDT & E International, 38(8), S. 701–711.
[10] ISO (23865): ISO/DIS 2020 -FMC-TFM - General Use of TFM-FMC Technique.
[11] P. Johnson (2019): „With a New Software Wizard, There’s No Sorcery but the Magic of the M2M Gekko Is Evident with Instant Code Compliance for Your TFM Weld Inspections.” In: Code Compliant TFM Weld Inspection with Three Clicks.
[12] ASME Committee (2019): „ASME BPVC.V Article 4 Nonmandatory Appendix F - Examination of Welds Using Full Matrix Capture.”