2.5 波前动态
Formación de frente de onda
Mientras que una sonda monoelemento puede ser considerada como un pistón, un solo disco o una placa que es impulsada hacia el material de ensayo, la onda que genera puede ser modelada matemáticamente como la suma de las ondas desde un amplia cantidad de fuentes puntuales. Esto deriva del principio de Huygens. Christiaan Huygens fue un físico neerlandés del siglo XVII quién estableció inicialmente que cada punto de un frente de onda que avanza puede ser considerado como una fuente puntual, la cual genera una nueva onda esférica y el frente de onda unificado resultante es la suma de todas las ondas esféricas individuales.
Dispersión del haz
En teoría, una onda acústica generada por una sonda se propagará en línea recta hasta encontrar un obstáculo o límite en el material. La segunda etapa se explica a continuación. Pero si la longitud del camino es más extenso que la distancia de campo cercano, el haz sólo aumentará en diámetro, diseminándose como el haz de un proyector. El ángulo de dispersión del haz, emitido por una sonda desenfocada, puede ser calculado de la siguiente manera:

A partir de esta ecuación es posible visualizar que la dispersión del haz incrementa con frecuencias más bajas y diámetros más pequeños. Un haz que mantiene un gran ángulo de dispersión puede causar, según la distancia, una rápida caída de la energía de sonido por unidad inspeccionada, como también la disminución de la sensibilidad en pequeños reflectores. Por ello, la respuesta de ecos en algunas aplicaciones donde intervienen largas trayectorias de sonido, puede ser optimizada al utilizar sondas de mayor frecuencia y diámetro.
Atenuación
Durante la propagación a través del medio, el frente de onda organizado que ha sido generado por una sonda de ultrasonido se dividirá debido a la transmisión imperfecta de la energía a través de microestructura de cualquier material. Las vibraciones mecánicas organizadas (ondas de ultrasonido) se transformarán en vibraciones mecánicas aleatorias (calor) hasta que el frente de sonda no pueda ser detectado. A este proceso se le conoce como atenuación de sonido.
La teoría matemática sobre la atenuación y dispersión es compleja. La pérdida de amplitud debido a la atenuación, en una trayectoria acústica específica, sería la suma de los efectos de absorción que incrementan la linealidad con la frecuencia, y los efectos de dispersión, que varían a través de tres zonas, según el tamaño del plano de exfoliación u otros reflectores de longitud de onda. En cualquiera de los casos, los efectos de dispersión incrementan con la frecuencia. En el caso de un material específico con una temperatura determinada, que está siendo inspeccionado mediante una frecuencia dada, existirá un coeficiente de atenuación específico que se expresa en neperios por centímetros (Np/cm). Cuando este coeficiente de atenuación es conocido, las pérdidas a través de una trayectoria pueden ser calculadas según la ecuación.

En la práctica, los coeficientes de atenuación durante las aplicaciones no destructivas por ultrasonido normalmente son medidos en lugar de ser calculados. Las frecuencias más altas serán atenuadas con mayor rapidez a diferencia de aquellas frecuencias más bajas. Por ello, las frecuencias de ensayo bajas normalmente son empleadas en materiales con mayores coeficientes de atenuación, tales como los plásticos y el caucho de baja densidad.
Reflexión y transmisión en un límite/obstáculo plano perpendicular
Cuando la onda, que se propaga a través de un medio, impacta con un límite u obstáculo que presenta un medio distinto y está orientado de manera perpendicular a la dirección de la onda, una porción de la energía de la onda se reflejará directamente y otra porción continuará. El porcentaje de la reflexión, a comparación de la transmisión, está relacionado con la impedancia acústica correspondiente a dos materiales. La impedancia acústica es a su vez definida como la densidad del material multiplicada por la velocidad del sonido. El coeficiente de reflexión en un límite u obstáculo plano y el porcentaje de la energía acústica, que vuelve a reflejarse en la fuente, deben ser calculados de la siguiente manera:

A partir de esta ecuación puede visualizarse que mientras las impedancias acústicas de dos materiales devienen más similares, el coeficiente de reflexión disminuye, y mientras las impedancias acústicas devienen menos similares, el coeficiente de reflexión aumenta. En teoría, la reflexión a partir del obstáculo o límite entre dos materiales que presentan la misma impedancia acústica es de cero. En el caso de materiales con impedancias acústicas muy diferentes, como un límite entre el acero y el aire, el coeficiente de reflexión se acercará a 100 %.
Refracción y conversión de modo en límites no perpendiculares.
Cuando una onda acústica se propaga a través de un material e impacta con el límite de un material diferente, obteniendo un ángulo superior a cero grados, una porción de la energía de la onda se reflejará en adelante con un ángulo igual al ángulo de incidencia. Al mismo tiempo, la porción de la energía de la onda que es transmitida a través del segundo material será refractada según la ley de Snell, la cual ha sido derivada independientemente por al menos dos matemáticos del siglo XVII. La ley de Snell relaciona los senos de los ángulos de incidencia y de los ángulos refractados con la velocidad de la onda en cada material, tal como es explicada a continuación.
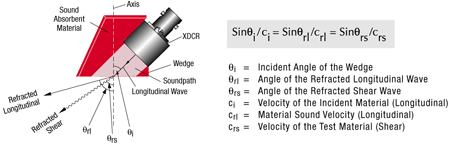
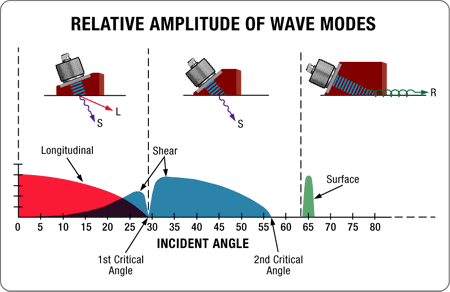
Si la velocidad del sonido en el segundo medio es superior a aquella del primero, sobre algunos ángulos, esta flexión será acompañada por la conversión de modo —frecuentemente de un modo de onda longitudinal a un modo de onda transversal. Esta es la base de la técnicas de inspección de haces angulares ampliamente utilizadas. Tal como en el caso de un ángulo de incidencia en el primer (más lento) medio —como una suela o agua— que aumenta, el ángulo de la onda longitudinal refractada en el segundo medio (más rápido) —como metales— también incrementará. Mientas el ángulo de onda longitudinal refractada se aproxima a 90 grados, una porción progresiva mayor de la energía de onda será convertida a una onda transversal de velocidad más baja. Ésta será refractada en el ángulo previsto por la ley de Snell. En ángulos de incidencia superiores, que pueden crear una onda longitudinal refracta de 90 grados, la onda refractada existe completamente en modo transversal. Aun así, un ángulo de incidencia superior puede presentar una situación donde la onda transversal es teóricamente refractada a 90 grados. A partir de este punto, una onda superficial será generada en el segundo medio o material. La siguiente secuencia muestra este efecto en el caso de un grupo de haz angular acoplado en acero.