包络功能使全聚焦方式更出色

Resumen

Este artículo expone cómo calcular la representación de la envolvente del método de focalización total (TFM) y los beneficios de usarla como parte de una solución conforme a las normativas en vigor. La envolvente TFM es obtenida por cálculo normativo de dos representaciones diferentes: en concreto, la primera es una representación del TFM calculada mediante la captura de matriz completa (FMC) estándar, y la segunda es una representación del TFM calculada mediante la FMC descrita por la transformada de Hilbert. La representación resultante de la envolvente TFM proporciona un mejor contexto para el método de dimensionamiento en función de la amplitud ya que es más fuerte para la variación de amplitud con respecto a una representación TFM oscilatoria estándar bajo una resolución idéntica de cuadrícula. Por lo tanto, con respecto a la representación TFM oscilatoria estándar, se puede determinar una resolución de cuadrícula más elevada (gruesa) para la envolvente TFM, lo que permite reducir la completa labor del cálculo e incrementa en última instancia la velocidad de adquisición resultante.

Introducción

El método de focalización total (TFM) es una técnica recientemente adoptada para evaluar materiales y estructuras de forma no destructiva. Ciertos estándares/códigos y normas ahora incluyen una sección sobre la captura de matriz completa (FMC) y el método de focalización total (TFM) para ensayos no destructivos (END) [1], [2].

Algunos dispositivos de ensayos no destructivos, como el detector de defectos OmniScan™ X3, permiten el procesamiento de representaciones por el TFM en tiempo real. La metodología del TFM con FMC se resume en las siguientes secciones; pero, la premisa de partida es que el TFM se basa en la suma de una multitud de valores de amplitud de formaciones de onda (A-scan) elementales. Las representaciones TFM son oscilatorias debido a ondas procedentes de representaciones A-scan elementales. Por otro lado, los esquemas de caracterización que se hallan en las aplicaciones de ensayos no destructivos son técnicas basadas esencialmente en la amplitud cuyo comportamiento oscilatorio puede ser visualizado como un artefacto acústico superfluo. Una práctica común para adaptar el comportamiento oscilatorio a los esquemas de caracterización es a través de la rectificación de la amplitud, de tal manera que la representación aparezca exclusivamente con valores positivos. Si bien este enfoque facilita la interpretación de representaciones en función de su equivalente completamente oscilante, este artículo mostrará cómo el uso de la envolvente de señal puede aligerar aún más el esfuerzo de caracterización e incrementar realmente la frecuencia de adquisición en relación con la representación TFM oscilatoria estándar.

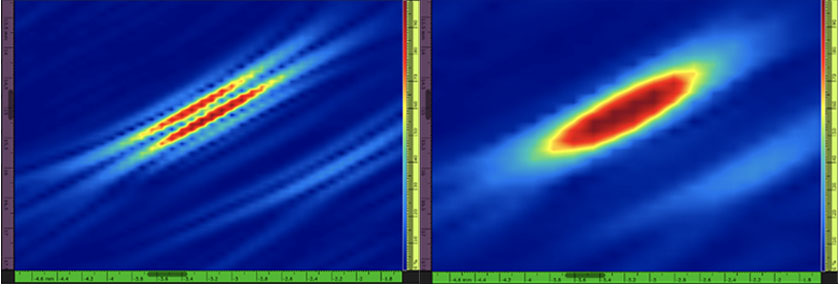
Figura 1: Izq. — Ejemplo de una imagen TFM de taladro de fondo plano (SDH) con valores de amplitud exclusivamente positivos y oscilación de señal (p. ej. representación TFM estándar).
La resolución de cuadrícula es 0,08 mm (λ / 8,1) y la amplitud máxima es de 108,7 %. Der. — Envolvente TFM del mismo taladro de fondo plano. La resolución de cuadrícula es 0,16 mm (λ / 4,0) y la amplitud máxima es de 122,6%.

Existen varias desventajas al usar representaciones TFM oscilatorias. La primera es la resolución de la cuadrícula TFM (p. ej., la distancia entre dos píxeles en la trama) que debe ser de aproximadamente λ / 8 en conformidad con las normas [1]–[3]. En este artículo, λ es la longitud de onda asociada a la frecuencia central de la sonda y, en parte, a la velocidad acústica. Una resolución de cuadrícula pequeña implica un gran esfuerzo de cálculo, lo que resulta de inmediato en una frecuencia de adquisición más baja. La fuerza asociada a los métodos de dimensionamiento en función de la amplitud es afectada por la representación TFM oscilatoria. Por lo tanto, la amplitud máxima de un eco medido es más fuerte según la compensación de fase de la señal adquirida.

Todas estas complejidades pueden resolverse usando la envolvente TFM ya que ella elimina las oscilaciones de señal en la representación y otorga una medición de amplitud máxima más fuerte (vea la Figura 1). La productividad de adquisición se beneficia al usar la envolvente TFM ya que requiere una resolución de cuadrícula reducida (p. ej., separación más amplia entre dos píxeles adyacentes) dotada de la misma fuerza de amplitud frente a la representación TFM estándar. Por ejemplo, una resolución de cuadrícula de aproximadamente λ / 4 es suficiente para la envolvente TFM la cual proporcionará la misma fidelidad de amplitud (2 dB) que la representación TFM oscilatoria estándar dotada de una resolución de λ / 8 [3].

El objetivo de este artículo es informar al especialista de ensayos no destructivos (END) sobre los beneficios que brinda el uso de la envolvente TFM. En la primera parte se presentará un resumen sobre la metodología FMC-TFM, seguida de los conceptos de cálculo que se atribuyen a la envolvente TFM. Por último, se presentaran los beneficios atribuidos al uso de la envolvente TFM como parte de una solución de conformidad normativa frente a las representaciones de tipo oscilatorio estándar.

Resumen de la metodología FMC-TFM

El sello distintivo de la tecnología de ultrasonido multielemento es su capacidad de enfoque en cualquier posición de una pieza bajo inspección. La técnica del ultrasonido multielemento (Phased Array) aplica retardos, ya sea en la emisión como en la recepción, para sincronizar el tiempo de vuelo de señales cortas impulsadas hacia la posición de interés. En el área focal de la muestra, la anchura completa del haz acústico generado deviene más pequeña y la resolución de detección correspondiente incrementa de forma radical [4]–[12].

El método de focalización total es una extensión natural de esta capacidad. Este produce un haz enfocado a través de la focalización de ultrasonido multielemento (Phased Array) y su dispersión en cada posición sobre una región de interés a nivel de la pieza inspeccionada; además, solo los puntos de datos focalizados altamente resueltos son presentados al operador [13]–[16]. A menudo, la región de interés consiste en una cuadrícula cartesiana uniforme de todos los objetivos de focalización requeridos. Obviamente, lograr esta focalización en cada posición de la cuadrícula, usando la técnica de formación física del haz de manera convencional, puede consumir tiempo debido al período de propagación acústica física que es requerido para alcanzar cada posición de interés.

Puesto que las ondas acústicas típicas del ultrasonido para las aplicaciones de END son lineales, el resultado de la formación física del haz, que resulta de la superposición de los campos acústicos actuales para todos los elementos contribuyentes en una apertura específica, puede ser imitado por un proceso de adquisición posterior basado en el conjunto de datos de la captura de matriz completa (FMC). La recuperación del conjunto de datos FMC requiere grabar la señal a partir de todos los elementos que componen la apertura recibida mientras una emisión acústica se genera por cada elemento individual incluida en dicha apertura de emisión. Como tal, el conjunto de datos FMC se forma por múltiples A-scan elementales en función de todas las combinaciones de los elementos emitidos y recibidos.

Obtener la amplitud focalizada a partir de una posición de enfoque específica, tal como en el caso del ultrasonido multielemento convencional, requiere lo siguiente:

• El cálculo del tiempo de vuelo requerido para la propagación acústica a fin de alcanzar la posición focal correspondiente a una posición de cuadrícula de interés seleccionada y regresar al elemento de recepción, dirigido a todos los pares de elementos de emisión y recepción de la apertura.
• La selección del punto de los datos de amplitud que corresponden al tiempo de vuelo apropiado y completo de emisión y recepción dirigido a todos los pares de elementos de emisión y recepción de la apertura.
• La adición de todos los puntos de datos de amplitud seleccionados sobre todos los elementos de emisión y recepción de las aperturas que hayan intervenido.
• La ubicación del resultado de la amplitud sumada en la posición de la cuadrículas que fue seleccionada inicialmente.

La repetición de estos pasos para todas las posiciones de la cuadrícula sobre la región de interés produce un mapa de amplitud cuya totalidad de valores de amplitud corresponden a un haz focalizado, ya sea en emisión y recepción. Este método para usar los datos FMC a fin de producir un mapa de amplitud focalizado en cada posición sobre la región de interés (p. ej. la zona TFM) es mencionado como metodología FMC-TFM.

¿Cómo se calcula la envolvente TFM?

Esta sección describe cómo se calcula la envolvente TFM usando los mismos A-scan elementales (FMC) que han sido adquiridos por el método de focalización total estándar. Note que la envolvente tiene una manifestación física y no es un simple algoritmo de afinamiento de imagen. La envolvente de la representación TFM tiene raíces en cada A-scan constituido. Primero, para ilustrar de forma esquemática su comportamiento, el concepto de envolvente es presentado usando una serie de tiempos de impulso de función gaussiana. El proceso también se aplica a un A-scan empírico y a una trama TFM completa.

La señal a(t) corresponde a la señal adquirida —por ejemplo, el equivalente de un A-scan elemental adquirido a través de la FMC— y es, de hecho, la parte real de una señal analítica compleja z(t) que puede ser formulada como sigue:

donde a’(t) corresponde a la parte imaginaria de la señal analítica, y θ(t) es la fase instantánea de la señal. La parte imaginaria es calculada de forma efectiva mediante la transformada de Hilbert [17]. La envolvente de la señal corresponde a la norma de señal analítica que puede ser formulada como sigue:

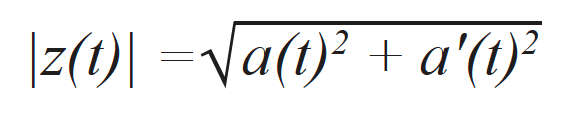
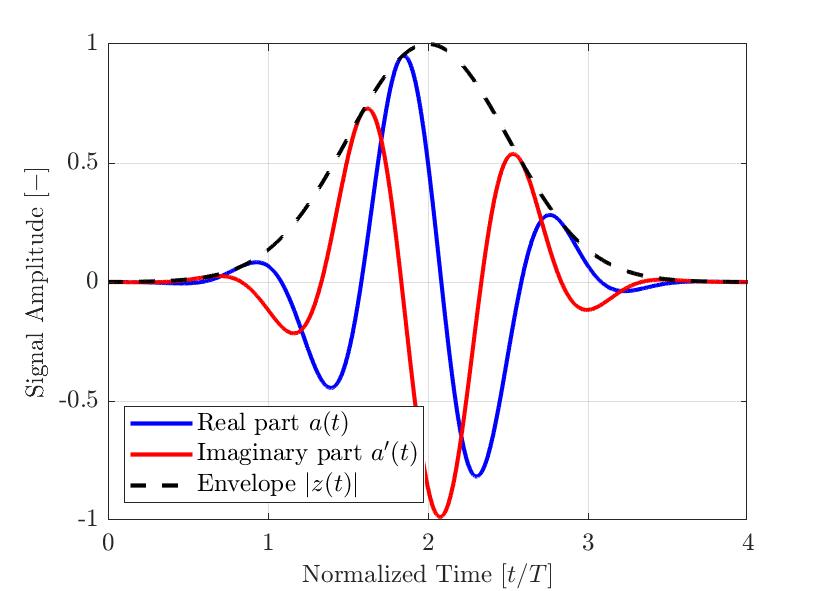
Figura 2: Impulso modulado gaussiano típico para aplicaciones de END Se muestran las partes reales e imaginarias y la envolvente calculada.
El eje de tiempo es normalizado con el período de frecuencia central seleccionado del impulso.

La Figura 2 se muestra como un ejemplo de un impulso modulado gaussiano a(t). La señal real a(t) aparece en azul; su parte imaginaria a’(t) tratada por la transformada de Hilbert aparece en rojo y la envolvente resultante |z(t)| aparece como línea discontinua. Tal como se ha visto en la ecuación anterior, la envolvente de la señal |z(t)| no es afectada por la fase θ(t) de la señal. Por lo tanto, las señales con diferentes desfases ϕ pueden tener la misma envolvente. La Figura 3 ilustra varios impulsos modulados gaussianos con diferentes desfases ϕ y su envolvente resultante. Por consiguiente, la amplitud máxima medida de la señal es más fuerte cuando se usa la envolvente de la señal a diferencia del valor absoluto del componente real de la señal analítica.

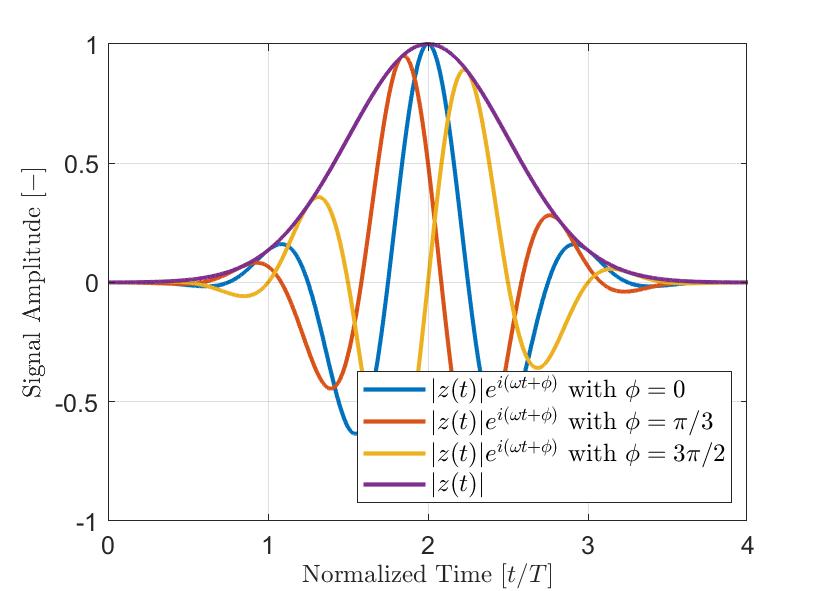
Figura 3: Impulsos modulados gaussianos típicos (|z(t)|e^i(ωt+ϕ)) con diferentes desfases ϕ. La envolvente |z(t)| de las señales es claramente independiente de la fase instantánea de la señal analítica.

El mismo proceso puede utilizarse para obtener la envolvente de un A-scan empírico. La Figura 4 muestra un A-scan elemental típico adquirido a través de la FMC, mientras que la Figura 5 muestra el mismo A-scan (azul) con su transformada de Hilbert (rojo) y la envolvente calculada (línea discontinua). Todas las señales mostradas están normalizadas al nivel máximo de la envolvente de la amplitud.

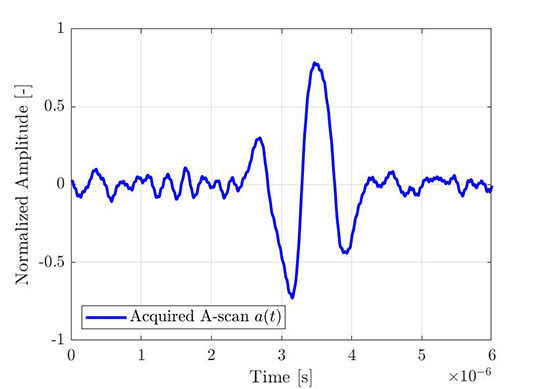Figura 4: Porción de un A-scan elemental adquirido (a partir de una adquisición FMC)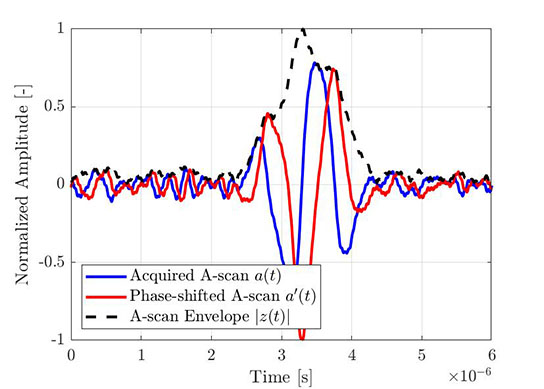

Figura 5: El mismo A-scan elemental con su transformada de Hilbert y la envolvente calculada.

La representación de la envolvente TFM —con índices de puntos individuales (k,l)— es calculada usando las señales analíticas de todos los A-scan que han contribuido [15]. En sí, el resultado del cálculo es la norma de una representación analítica TFM y(k,l) compuesta por la trama TFM estándar x(k,l) que ha sido calculada usando los datos estándar adquiridos por la FMC y una trama TFM x'(k,l) calculada con la transformada de Hilbert de los datos provenientes de la FMC. Para ambos casos se utiliza el mismo conjunto de retardos. La envolvente TFM pasa a ser calculada usando la siguiente expresión:

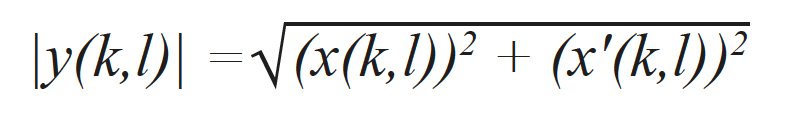
Por lo tanto, una representación de la envolvente TFM es el resultado de una combinación de dos representaciones TFM (vea la Figura 6): una proveniente del componente real a partir de los A‐scan elementales y la otra del componente imaginario calculado a partir de los A-scan elementales. Si bien este proceso carga el esfuerzo de cálculo y reduce la velocidad de adquisición del instrumento de ensayos no destructivos, en la siguiente sección se demuestra que la resolución de la cuadrícula requerida puede ser reducida significativamente sin afectar la fidelidad de la amplitud, lo cual aumenta la velocidad de adquisición a un nivel superior con respecto al uso de la representación TFM estándar.

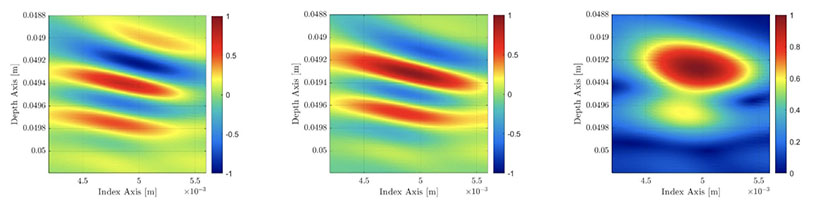
Figura 6: Izq. —Trama TFM estándar (no en el valor absoluto). Centro —Trama TFM calculada usando la transformada de Hilbert de la FMC. Der. —Representación de la envolvente TFM resultante.

Ventajas de usar la envolvente TFM

En esta sección, se demostrarán las ventajas de la envolvente TFM mediante la comparación de varias tramas TFM con diferentes índices de resolución de cuadrícula, que van desde λ / 9,3 hasta λ / 4,0, y la monitorización de indicadores de inspección críticos. Los resultados se obtuvieron usando una sonda 5L32-A31 y una suela (zapata) SA31-N55S-IHC en un bloque de acero con un taladro lateral (DSH) de de 1 mm de diámetro (vea la Figura 7). Se usó un gel de acoplamiento (Ultragel II de la empresa Sonotech) entre la suela (zapata) y el bloque de acero. Los datos fueron adquiridos con un detector de defectos OmniScan™ X3 de Olympus. Se seleccionó la trayectoria acústica de pulso-eco (T-T) y la dimensión de área (20 mm × 20 mm). La longitud de onda asociada a la pieza y trayectoria acústica que se seleccionó es λ = 0,648 mm. La resolución de la cuadrícula es anotada en términos de fracción de longitud de onda.

Figura 7: Foto de la configuración empleada para adquirir las representaciones TFM de la Tabla 1. El rectángulo azul corresponde a toda la región de interés (20 mm × 20 mm) mientras que el rectángulo rojo corresponde a la región de interés ampliada (5 mm × 5 mm) que se muestra en las representaciones de la Tabla 1. La sonda 5L32-A31 y la suela (zapata) SA31-N55S-IHC fueron usadas. El bloque de acero era de 40 mm de espesor.

La tabla 1 muestra las representaciones TFM resultantes para cuatro valores de resolución de cuadrícula diferentes, que van desde λ / 9,3 a λ / 4,0, tanto para la representación TFM estándar como para la representación de la envolvente TFM. El valor de fidelidad de amplitud computada [3] y la tasa de adquisición resultante se indican en cada una de las imágenes TFM.

Resolución de cuadrícula	TFM estándar	Envolvente TFM
λ / 9,3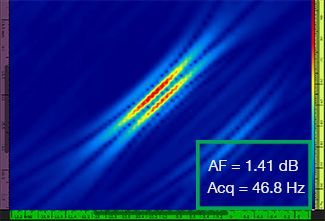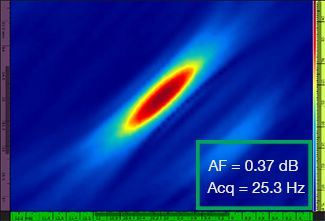
λ / 8,1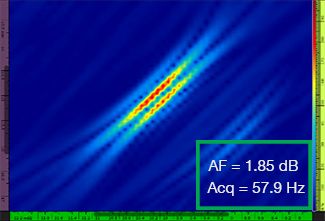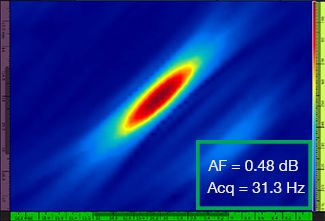
λ / 5,9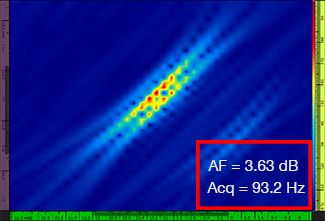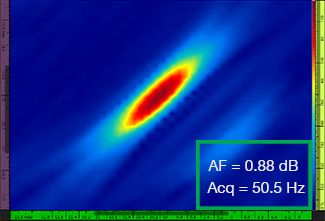
λ / 4,0

Los nuevos códigos y normas disponibles [1, 2] requieren que el valor de fidelidad de amplitud sea igual o inferior a 2 dB. Por lo tanto, sólo los dos primeros valores de resolución de cuadrícula (λ / 9,3, λ / 8,1) son conformes a la normativa cuando se utiliza la representación TFM estándar. La envolvente del TFM permite una resolución de cuadrícula más alta (gruesa) [λ / 4.0] manteniendo una fidelidad de amplitud conforme a la normativa. A su vez, el uso de la envolvente TFM con una cuadrícula más gruesa conlleva al aumento de la velocidad de adquisición un 37 % aprox. con respecto a la frecuencia de adquisición más elevada que se ha logrado mediante la representación TFM estándar conforme a la normativa (57,9 Hz en λ / 8,1).

Conclusiones

En esta publicación se ha presentado e ilustrado con ejemplos sencillos el método para calcular la envolvente de una representación TFM. Se demostró que la envolvente de una señal es independiente de su fase instantánea y, por lo tanto, proporciona una base más sólida para las técnicas de dimensionamiento basadas en la amplitud (como el método de caída de 6 dB). La envolvente de la señal no es simplemente un afinamiento de imagen y no debe considerarse como un filtro cuya aplicación puede generar pérdidas de datos. Las ventajas de utilizar la envolvente en las representaciones TFM se demostraron mediante comparaciones de representaciones TFM, con y sin la envolvente, en función de diferentes valores de resolución de cuadrícula. Aunque dos representaciones TFM deben ser calculadas para obtener la envolvente TFM resultante, la carga del procesamiento puede reducirse significativamente utilizando una resolución de cuadrícula más gruesa sin ir en contra del cumplimiento normativo. Esto se debe a la fuerza de la envolvente en cuanto a la variación de la amplitud. El resultado es una representación más adaptada al tamaño de la amplitud, pero obtenida a un ritmo más rápido que la imagen equivalente procesada con la representación TFM estándar.

Referencias

[1] Comité ASME, «ASME BPVC.V Article 4 Mandatory Appendix XI Full Matric Capture.» ASME, 2019.

[2] Comité ASME, «ASME BPVC.V Article 4 Nonmandatory Appendix F - Examination of Welds Using Full Matric Capture.» ASME, 2019.

[3] N. Badeau, A. Le Duff, y C.-H. Kwan, «Theoretical Model for Amplitude Fidelity Reading (submitted),» presentado en el Simposium de investigación ASNT, 2020.

[4] A. C. Clay, S.-C. Wooh, L. Azar y J.-Y. Wang, «Experimental Study of Phased Array Beam Steering Characteristics,» Journal of Nondestructive Evaluation, vol. 18, N.º 2, pág. 13, 1999.

[5] L. J. Bond, «Fundamentals of Ultrasonic Inspection,» ASM Handbook, vol. 17, N.º Nondestructive Evaluation of Material, págs. 155–168, 2018.

[6] S.-J. Song, H. J. Shin e Y. H. Jang, «Development of an ultra sonic phased array system for nondestructive tests of nuclear power plant components,» Nuclear Engineering and Design, vol. 214, N.º 1–2, págs. 151–161, Mayo 2002, doi: 10.1016/S0029-5493(02)00024-9.

[7] S. Mahaut, O. Roy, C. Beroni y B. Rotter, «Development of phased array techniques to improve characterization of defect located in a component of complex geometry,» Ultrasonics, vol. 40, N.º 1–8, págs. 165–169, Mayo de 2002, doi: 10.1016/S0041-624X(02)00131-2.

[8] S. C. Mondal, P. D. Wilcox y B. W. Drinkwater, «Design of Two-Dimensional Ultrasonic Phased Array Transducers,» Journal of Pressure Vessel Technology, vol. 127, N.º 3, págs. 336–344, Agosto de 2005, doi: 10.1115/1.1991873.

[9] S.-C. Wooh y Y. Shi, «Influence of phased array element size on beam steering behavior,» Ultrasonics, vol. 36, N.º 6, págs. 737–749, Abril de 1998, doi: 10.1016/S0041-624X(97)00164-9.

[10] Joon-Hyun Lee y Sang-Woo Choi, «A parametric study of ultrasonic beam profiles for a linear phased array transducer,» IEEE Trans. Ultrason., Ferroelect., Freq. Contr., vol. 47, N.º 3, págs. 644–650, Mayo de 2000, doi: 10.1109/58.842052.

[11] R. Ahmad, T. Kundu y D. Placko, «Modeling of phased array transducers,» The Journal of the Acoustical Society of America, vol. 117, N.º 4, págs. 1762–1776, Abril de 2005, doi: 10.1121/1.1835506.

[12] B. W. Drinkwater y P. D. Wilcox, «Ultrasonic arrays for non-destructive evaluation: A review,» NDT & E International, vol. 39, N.º 7, págs. 525–541, Octubre 2006, doi: 10.1016/j.ndteint.2006.03.006.

[13] P. D. Wilcox, «Exploiting the Full Data Set from Ultrasonic Arrays by Post-Processing,» en Actas de conferencias AIP, Brunswick, Maine (EE. UU.), 2006, vol. 820, págs. 845–852, doi: 10.1063/1.2184614.

[14] J. Zhang, B. W. Drinkwater y P. D. Wilcox, «Effects of array transducer inconsistencies on total focusing method imaging performance,» NDT & E International, vol. 44, N.º 4, págs. 361–368, Julio de 2011, doi: 10.1016/j.ndteint.2011.03.001.

[15] C. Holmes, B. W. Drinkwater y P. D. Wilcox, «Advanced post-processing for scanned ultrasonic arrays: Application to defect detection and classification in non-destructive evaluation,» Ultrasonics, vol. 48, N.º 6–7, págs. 636–642, Nov. 2008, doi: 10.1016/j.ultras.2008.07.019.

[16] C. Holmes, B. W. Drinkwater y P. D. Wilcox, «Post-processing of the full matrix of ultrasonic transmit–receive array data for non-destructive evaluation,» NDT & E International, vol. 38, N.º 8, págs. 701–711, Diciembre de 2005, doi: 10.1016/j.ndteint.2005.04.002.

[17] D. Gabor, «Theory of Communication,» Journal of the Institution of Electrical Engineers, vol. 96, págs. 429–441, 1946.