Auteurs : Nicolas Badeau, Guillaume Painchaud-April et Chi-Hang Kwan
Résumé
La technique d’inspection du nom de « méthode de focalisation en tout point » (TFM) est désormais incluse dans les codes et les normes qui régissent les contrôles non destructifs (CND). C’est le cas par exemple dans la section V du code ASME. L’un des paramètres importants indiqués dans ces codes pour l’établissement du plan d’inspection TFM est la fidélité en amplitude. Celle-ci se définit comme la variation d’amplitude obtenue pour un réflecteur en particulier, étant donné la résolution limitée de la grille d’imagerie. Le seuil de fidélité en amplitude généralement permis dans ces codes est de 2 dB au maximum. Bien que les codes proposent des méthodes expérimentales pour mesurer la fidélité en amplitude d’une configuration donnée, nous proposons dans cet article une méthode analytique à la fois simple et prudente. L’utilisation de l’enveloppe TFM est également prise en compte dans l’estimation de la fidélité en amplitude, car elle permet l’utilisation d’une grille TFM moins dense sans que la valeur de fidélité en amplitude dépasse la tolérance établie. Pour l’imagerie TFM standard, les résultats empiriques ont montré qu’une résolution de grille d’environ λ0/10 est nécessaire pour obtenir une fidélité en amplitude inférieure à 2 dB. Pour l’imagerie TFM avec l’enveloppe, les résultats empiriques ont montré la nécessité d’une résolution de grille de λ0/3,3 pour assurer la conformité au code.
Introduction
La méthode de focalisation en tout point (TFM) est une technique nouvellement acceptée pour les contrôles non destructifs (CND) des composants. En effet, les normes et les codes, comme le code ASME (section V) [1], intègrent maintenant l’utilisation de l’acquisition de la matrice intégrale (FMC) et de la TFM comme technique supplémentaire d’inspection par ultrasons multiéléments. Bien que la méthode FMC/TFM soit relativement nouvelle dans l’industrie du CND, elle est utilisée depuis un certain temps dans les applications médicales, où elle constitue la référence en matière d’imagerie médicale par ultrasons [2–4]. En effet, la plupart des techniques d’imagerie médicale par ultrasons sont habituellement comparées à l’imagerie TFM.
Bien qu’il existe plusieurs techniques similaires à la méthode FMC/TFM (par exemple, VTFM [5], IWEX [6] et SAFT [7]), l’algorithme le plus couramment utilisé est le traitement du retard et de la sommation [2–4,8,9]. La méthode FMC/TFM se fait sur la base d’un schéma d’acquisition (FMC), qui repose sur l’acquisition du signal de toutes les combinaisons d’éléments émetteurs et récepteurs, et d’un schéma de sommation (TFM), qui calcule le résultat du faisceau ultrasonore focalisé à plusieurs emplacements dans une région d’intérêt. La région d’intérêt de la TFM est souvent maillée sur une grille cartésienne, et les intersections individuelles de la grille auxquelles la focalisation acoustique est appliquée sont appelées « pixels ». La méthode de focalisation est similaire à l’imagerie par ultrasons multiéléments standard, sauf que les faisceaux sont formés en post-traitement à l’aide des données stockées dans la matrice de données FMC. Le traitement du retard et de la sommation post-acquisition suppose la linéarité des ondes acoustiques sous-jacentes que l’on retrouve dans les applications de CND habituelles.
La méthode FMC/TFM peut être considérée comme une extension naturelle de la technique multiélément classique. Toutefois, de nouveaux paramètres de configuration doivent être pris en compte en raison des différences dans la représentation des données par rapport à l’inspection par ultrasons multiéléments (PAUT). L’un de ces nouveaux concepts est la « fidélité en amplitude » (FA) d’une grille TFM. La FA se définit comme la variation d’amplitude maximale d’une indication causée par la résolution de la grille TFM {Δx,Δz}. Le reste de cette étude s’appuie sur l’utilisation d’une grille cartésienne uniforme, c’est-à-dire (Δx=Δz). La fidélité en amplitude peut être formellement exprimée ainsi :
![(Éq. 1) FA(Δx)≡-20 log〖(A_(max. échantillonnée) (Δx))/A_(max. réelle) 〗 [dB]](https://industrial.evidentscientific.com.cn/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_01.jpg?rev=43A1)
où Amax. échantillonnée est l’amplitude maximale mesurée d’un élément d’intérêt basé sur un échantillonnage limité de la grille, et Amax. réelle est le maximum du même élément d’intérêt basé sur une résolution infinie de la grille. La limite à laquelle la taille de la grille devient zéro sur les deux axes pour Amax. échantillonnée (Δx) définit Amax. réelle, et la fidélité en amplitude correspondante devient 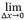 FA(Δx)=0. L’équation 1 fournit une définition formelle pour calculer la fidélité en amplitude par rapport à la résolution de la grille. Dans la pratique, cependant, la Amax. réelle du signal sous-jacent ne peut être estimée que par suréchantillonnage de l’image d’amplitude TFM et par interpolation,
FA(Δx)=0. L’équation 1 fournit une définition formelle pour calculer la fidélité en amplitude par rapport à la résolution de la grille. Dans la pratique, cependant, la Amax. réelle du signal sous-jacent ne peut être estimée que par suréchantillonnage de l’image d’amplitude TFM et par interpolation,
![(Éq. 2) (FA) (Δx)= -20 log〖(A_(max. échantillonnée) (Δx))/A_(max. réelle) 〗 [dB]](https://industrial.evidentscientific.com.cn/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_02.jpg?rev=43A1)
où A max. réelle est une estimation d’Amax. réelle.
max. réelle est une estimation d’Amax. réelle.
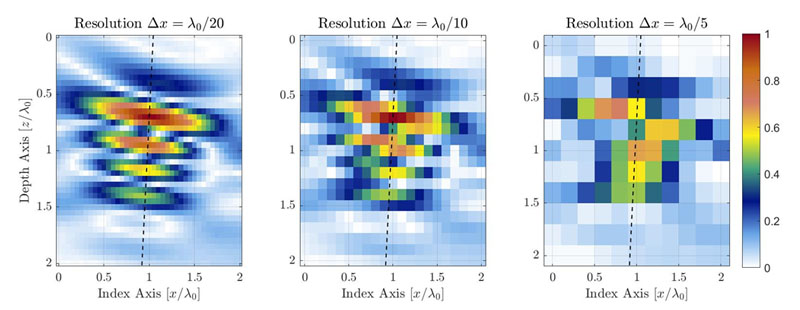
Figure 1 : Illustration de la dégradation de la qualité de l’image TFM causée par la diminution de la résolution de la grille TFM.
Les lignes pointillées représentent l’axe principal de la propagation acoustique.
Pour une zone d’intérêt identique, une résolution de grille plus grossière aura un nombre de pixels plus faible. La figure 1 montre des images TFM typiques du même trou percé latéral (SDH) pour différentes valeurs de résolution de grille. La résolution de grille se définit comme une fraction de la longueur d’onde de la fréquence centrale de la sonde λ0= c/f0, où c est la vitesse de propagation des ondes ultrasons dans la pièce et f0 la fréquence centrale de la sonde.
Les normes et les codes exigent désormais que la fidélité en amplitude ne dépasse pas les 2 dB [1,10]. Cette exigence découle du compromis applicatif entre une qualité d’image suffisante pour garantir une analyse CND appropriée et la productivité de l’inspection, qui est profondément affectée par la densité de la grille TFM sur une région d’intérêt donnée. Notez que le compromis entre la qualité d’image TFM et la productivité de l’inspection est particulièrement important pour les appareils portatifs autonomes qui ne disposent pas d’une grande puissance de traitement. Ce problème devrait disparaître progressivement, à mesure que l’efficacité énergétique du matériel s’améliorera et que les calculs à distance deviendront plus largement disponibles.
Bien que certaines méthodes empiriques aient été proposées [10–12], elles nécessitent habituellement des calculs poussés, et les résultats obtenus ne sont pas représentatifs de l’amplitude réelle causée par la résolution de la grille, un problème que nous expliquons dans la section suivante. Cet article présente une méthode permettant d’estimer avec précision la fidélité en amplitude d’une configuration TFM afin d’aider le technicien en CND à effectuer une inspection TFM à la fois conforme aux codes et productive.
L’article est divisé comme suit : tout d’abord, une explication complète du problème rencontré par les techniciens en CND est exposée. Ensuite, une méthode permettant de mesurer empiriquement la fidélité en amplitude d’une configuration TFM est décrite. Un modèle analytique permettant d’estimer la fidélité en amplitude est proposé dans la section suivante. Le modèle proposé est ensuite comparé à des mesures empiriques pour trois situations d’utilisation de la TFM. Enfin, une brève conclusion est donnée, résumant le travail effectué.
Description de la problématique
Alors qu’une grille très fine (c.-à-d. dense) permet une très faible fidélité en amplitude, les dispositifs électroniques contemporains capables de calculer des images TFM en temps réel souffrent encore de limites de calcul. Une résolution de grille plus fine sur une région d’intérêt donnée est synonyme d’un grand nombre de points de focalisation à calculer, ce qui entraîne une diminution de la productivité de l’inspection et de la vitesse des balayages mécaniques. Le technicien en CND doit être en mesure de sélectionner une résolution de grille appropriée qui maximise la productivité de l’inspection tout en assurant le respect des codes.
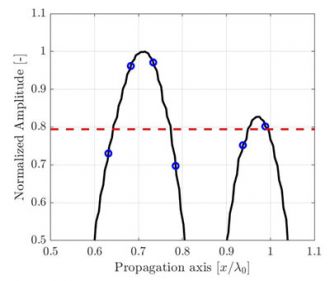
La fidélité en amplitude peut être illustrée par un simple échantillon de signal unidimensionnel prélevé à différentes périodes. Dans l’exemple montré à la figure 2, le signal unidimensionnel illustré représente l’amplitude du SDH présenté à la figure 1 le long de l’axe de propagation acoustique, provenant d’une image à haute résolution λ0/100. Seule une partie agrandie, près de l’amplitude maximale du signal, est présentée aux fins de cet exemple. Là encore, les mesures à trois résolutions différentes, soit λ0/20, λ0/10 et λ0/5, sont identifiées par des cercles bleus sur une référence interpolée en haute résolution (courbe noire continue).
(a) La résolution de grille discrète est λ0/20, et la fidélité en amplitude calculée est FA = 0,27 dB. |
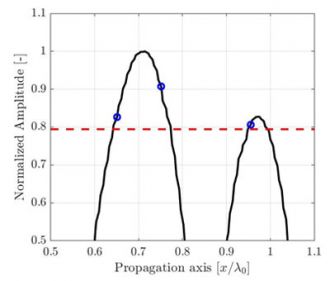
(b) La résolution de grille discrète est λ0/10, et la fidélité en amplitude calculée est FA = 0,82 dB. |
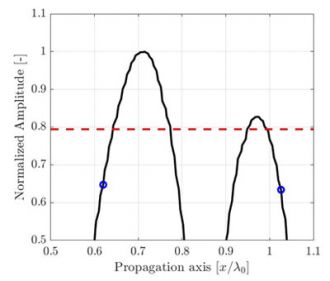
(c) La résolution de grille discrète est λ0/5, et la fidélité en amplitude calculée est FA = 3,7 dB. |
Figure 2 : Illustration de l’effet de la période d’échantillonnage sur l’amplitude enregistrée le long de l’axe de propagation illustré à la figure 1.
Une référence de signal interpolée en haute résolution (ligne noire) est illustrée pour faciliter la lecture.
La fidélité en amplitude conforme aux codes (2 dB) est représentée par une ligne rouge pointillée.
La conclusion évidente que l’on peut tirer, c’est qu’une grille plus dense fournit une meilleure représentation d’un signal continu, tel que quantifié selon la valeur FA de l’équation 1, mais le problème d’optimisation demeure : quelle est la taille de grille maximale (Δxmax) garantissant, pour toutes les positions de grille possibles sur une image TFM, une fidélité en amplitude  égale à une valeur cible FAcible ? Ou,
égale à une valeur cible FAcible ? Ou,
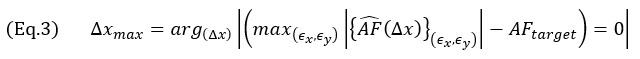
Il ressort clairement de cet énoncé du problème que toutes les translations de la grille, identifiées par les déplacements (ϵx,ϵy), doivent être prises en compte pour obtenir la valeur  maximale pour une taille de cellule fixe (Δx). L’objectif est de couvrir tous les cas possibles de placements de la grille pour calculer l’image TFM.
maximale pour une taille de cellule fixe (Δx). L’objectif est de couvrir tous les cas possibles de placements de la grille pour calculer l’image TFM.
La section suivante illustre le principe de mesure de l’ensemble des valeurs de fidélité en amplitude produites à partir de plusieurs déplacements de la grille { (Δx)}(ϵx,ϵy).
(Δx)}(ϵx,ϵy).
Mesure empirique de la fidélité en amplitude
Avant de présenter comment on peut estimer la fidélité en amplitude au moyen d’un modèle analytique simple, il est d’une importance capitale de définir la façon de la mesurer de façon expérimentale dans le cas d’une image TFM. Plusieurs techniques ont été décrites et proposées dans le secteur du CND [10–12], mais certaines d’entre elles ne quantifient pas la fidélité en amplitude de manière complète. La mesure empirique de la fidélité en amplitude peut rapidement devenir un travail d’acquisition très fastidieux pour le technicien en CND, car elle nécessite le calcul d’un grand nombre d’images TFM à partir de plusieurs positions précises de la grille TFM.
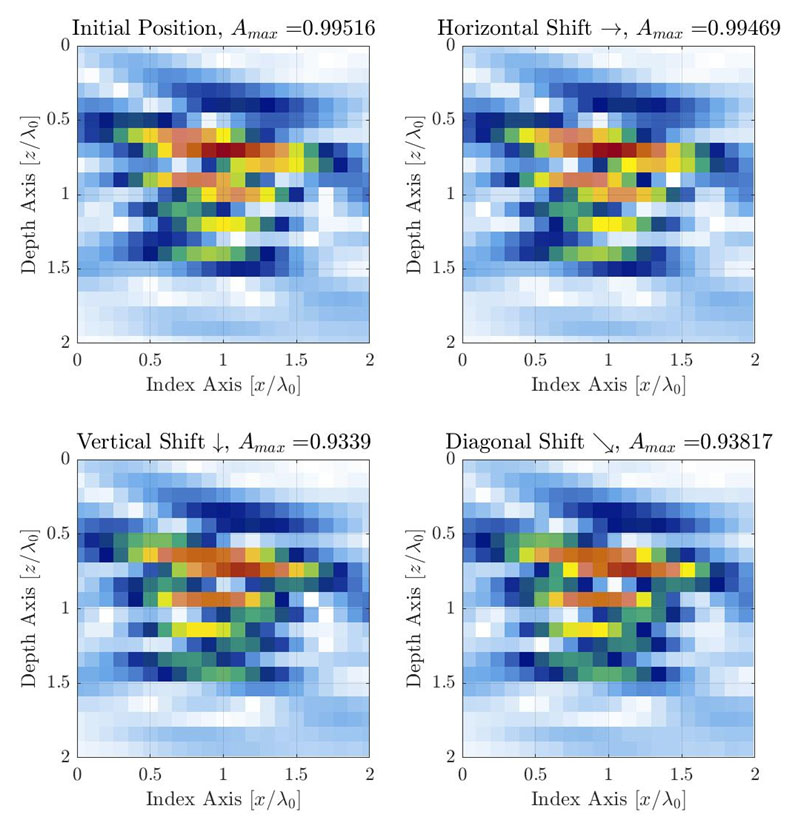
Figure 3 : Illustration de la variation de la FA causée par la résolution de grille discrète lorsque l’on déplace la grille dans 3 directions différentes. La résolution de la grille est définie sur Δx=Δy=λ0/10. La grille est décalée d’un quart de la cellule de la grille vers la droite (ϵx=λ0/40,ϵy=0) (en haut à droite), vers le bas (ϵx=0,ϵy=λ0/40) (en bas à gauche) et en diagonale (ϵx=λ0/40,ϵλ y=0/40) (en bas à droite).
Pour les applications TFM habituelles, un SDH est utilisé comme défaut de référence pour l’étalonnage de l’amplitude et la mesure de la fidélité en amplitude [1,10]. L’amplitude observée varie le plus le long de l’axe principal de la propagation acoustique, qui est fonction de la sonde, du sabot et de la position cible dans la région d’intérêt (c.-à-d. la position de la grille TFM par rapport à la sonde). Dans le cas illustré à la figure 1, le principal axe de propagation est presque vertical. Toutefois, pour une méthode de mesure générique, l’axe de propagation sera différent selon l’emplacement dans la région d’intérêt. Pour une image TFM, la grille d’échantillonnage doit être déplacée dans toutes les directions pour relever la variation d’amplitude réelle causée par la grille discrète. Ce processus est illustré ci-dessous avec le même exemple que pour la figure 1 (centre), qui a une résolution de grille de λ0/10.
Il est recommandé de déplacer la grille d’une petite fraction de la résolution de la grille à tester (p. ex. d’environ un vingtième de la résolution) dans toutes les directions, autant de fois que nécessaire pour obtenir le chevauchement de la grille. Cela signifie que pour couvrir un décalage de la résolution d’une grille dans les deux directions orthogonales, un total de 202 = 400 pas de déplacement s’avère nécessaire (en utilisant le pas de grille suggéré d’un vingtième de la résolution). L’amplitude maximale est enregistrée pour chaque décalage de la grille et les valeurs maximale et minimale relevées sont utilisées pour obtenir la fidélité en amplitude au moyen de l’équation 2. Dans le cas présenté à la figure 3, la résolution de la grille est de λ0/10, et la fidélité en amplitude mesurée est de 0,88 dB. Si l’on en juge par le nombre de déplacements que cela nécessite, ce processus manuel serait fastidieux et chronophage pour le technicien en CND. Cela signifie également qu’un total de 400 images TFM devrait être calculé pour mesurer la fidélité en amplitude d’une résolution d’une seule grille.
Il convient de mentionner qu’en utilisant un déplacement logiciel de la position de la grille TFM par rapport à la sonde au lieu d’un déplacement mécanique de la sonde par rapport à la pièce comme proposé dans la section V du code ASME [12], de multiples images TFM peuvent être générées à l’aide d’un seul ensemble de données FMC. Autre avantage de cette approche : la possibilité d’accéder à la composante verticale de la grille. En effet, la sonde et le sabot ne peuvent pas être déplacés mécaniquement par rapport au SDH sélectionné le long de l’axe de profondeur.
Certains appareils de CND fournissent des outils semi-automatisés prêts à l’emploi qui déplacent la grille TFM, enregistrent l’amplitude maximale dans la région d’intérêt, puis calculent la fidélité en amplitude résultante [11]. Toutefois, ces outils ne déplacent généralement la grille que dans la direction horizontale et sous-estiment donc la fidélité en amplitude. À titre de comparaison, si la grille est déplacée uniquement le long de l’axe horizontal, par exemple, comme illustré à la figure 3, la fidélité en amplitude mesurée est de 0,06 dB, soit plus de 15 fois inférieure à la fidélité en amplitude mesurée lorsque l’on tient compte de l’axe vertical.
Un modèle phénoménologique pour l’estimation de la fidélité en amplitude
Cette section propose un modèle analytique simple basé sur l’observation empirique. Le modèle phénoménologique tient compte du comportement du signal le long de l’axe principal de propagation, qui est supposé contenir la majeure partie des fluctuations d’amplitude et, par conséquent, être le plus sensible à la résolution de la grille. La figure 4 montre le profil empirique d’une image TFM résultante pour un SDH situé le long de l’axe principal de propagation (en bleu) et le long de l’axe de la taille du faisceau (en rouge). L’origine de l’axe est située à l’emplacement de l’amplitude maximale apparente de la représentation de l’enveloppe, ce qui explique le petit décalage le long de l’axe  pour la représentation oscillatoire. Les profils de la TFM oscillatoire standard et de l’enveloppe de la TFM sont indiqués.
pour la représentation oscillatoire. Les profils de la TFM oscillatoire standard et de l’enveloppe de la TFM sont indiqués.
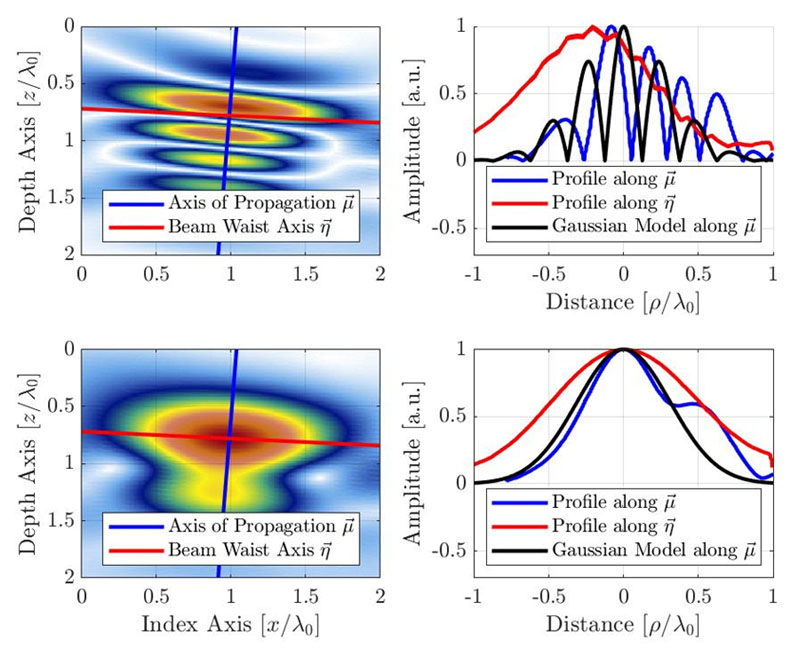
Figure 4 : Image TFM (en haut : oscillatoire, en bas : enveloppe) avec le profil de signal le long de l’axe de propagation acoustique et de l’axe de la taille du faisceau. Le modèle gaussien proposé est également illustré pour les images de la TFM oscillatoire et de l’enveloppe TFM. On constate que la longueur d’onde apparente est réduite de moitié en raison de la nature à écho d’impulsion de la formation du faisceau TFM.
Comme indiqué précédemment, la plus grande variation d’amplitude est supposée se trouver le long de l’axe principal de la propagation acoustique. Le modèle vise donc à reproduire la variation d’amplitude dans cette direction. Le signal du modèle est une gaussienne modulée par cosinus
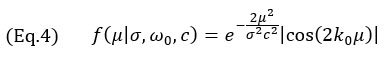
où k0=ω0/c est le nombre d’onde à la fréquence angulaire centrale ω0 de la sonde, et σ le paramètre de largeur dépendant de la fréquence centrale et de la largeur de bande relative bw. Le paramètre de largeur σ est calculé avec
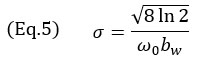
Pour une sonde CND multiélément type, la largeur de bande relative est proche des 60 %, ce qui explique pourquoi une valeur de (bw=0,6) est utilisée dans le modèle. Ceci, à son tour, rend l’enveloppe gaussienne plus grande qu’une oscillation unique de la fonction cosinus. Il convient de mentionner que la fréquence centrale du terme cosinus dans l’équation 3 est doublée par rapport à la fréquence centrale de la sonde. Cela s’explique par la nature à écho d’impulsion de l’imagerie TFM (trajectoire d’émission et de réception) et peut être observé dans la distance entre les oscillations de la figure 4. En fait, la conversion entre le domaine temporel et le domaine spatial s’écrit sous la forme μ = tc/2. Cela explique également le facteur 2 utilisé comme terme exponentiel de l’équation 3.
Pour le modèle oscillatoire de l’équation 4, étant donné que l’enveloppe gaussienne est beaucoup plus grande qu’une oscillation unique de la fonction cosinus, seules les valeurs |μ|≤λ0/8 sont prises en compte, car des valeurs plus grandes produisent un crénelage spatial pour la fidélité en amplitude.
Pour le modèle d’enveloppe TFM, seul le terme gaussien de l’équation 4 est utilisé, ce qui donne ce qui suit :
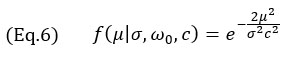
équation valable pour toutes les résolutions de grille. Le profil obtenu avec le modèle des équations 3 et 7 est illustré à la figure 4 en plus des profils expérimentaux. Notez que les mesures empiriques montrent également que le signal de l’onde de surface (l’écho « enveloppant » typique des SDH) accuse un retard par rapport à l’écho principal, une caractéristique clairement absente du modèle proposé.
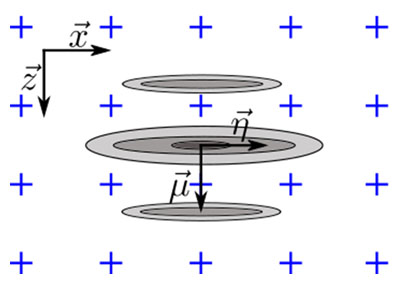
L’orientation du défaut par rapport aux axes orthogonaux de la grille doit être prise en compte de façon à obtenir le scénario de fidélité en amplitude le plus défavorable pour le modèle. Comme l’illustre la figure 5a, le scénario le plus défavorable pour la TFM oscillatoire se produit lorsque l’axe principal de la propagation acoustique  est parallèle à l’un des axes de la grille. Par conséquent, la fidélité en amplitude doit être calculée comme si l’amplitude maximale était centrée entre deux points de la grille le long de l’axe
est parallèle à l’un des axes de la grille. Par conséquent, la fidélité en amplitude doit être calculée comme si l’amplitude maximale était centrée entre deux points de la grille le long de l’axe 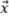 ou
ou 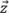 , ce qui donne
, ce qui donne
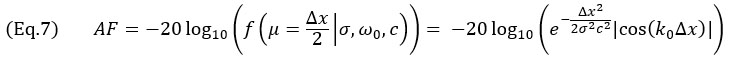
pour Δx≤λ0/4. Pour l’enveloppe TFM, le scénario le plus défavorable se produit lorsque le profil d’amplitude est identique le long de l’axe principal de propagation  et de l’axe de la taille du faisceau
et de l’axe de la taille du faisceau 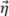 . Ce cas, illustré à la figure 5b, correspond au moment où le SDH est représenté par un cercle et, par conséquent, l’axe principal de propagation
. Ce cas, illustré à la figure 5b, correspond au moment où le SDH est représenté par un cercle et, par conséquent, l’axe principal de propagation  peut avoir n’importe quelle orientation. Le scénario le plus défavorable se produit lorsque l’écho SDH est centré entre quatre points adjacents, comme illustré. Dans ce cas, la fidélité en amplitude doit être calculée le long de la diagonale de la grille, ce qui donne concrètement
peut avoir n’importe quelle orientation. Le scénario le plus défavorable se produit lorsque l’écho SDH est centré entre quatre points adjacents, comme illustré. Dans ce cas, la fidélité en amplitude doit être calculée le long de la diagonale de la grille, ce qui donne concrètement
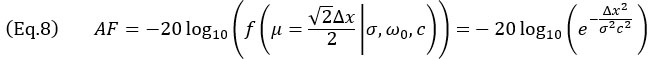
Une forme approximative de la valeur de Δx par rapport FA, dans les cas où la valeur FA est faible (ce qui est le scénario d’utilisation type pour les applications de CND), peut être obtenue pour le modèle oscillatoire de l’équation 7,

et pour le modèle de l’enveloppe de l’équation 8,
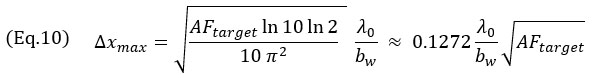
Ces expressions traduisent, dans tous les cas, la dépendance, pour la taille de la grille, entre la racine carrée et la valeur FA. L’équation 9 a été obtenue en utilisant l’approximation de la série de Taylor de deuxième ordre pour l’équation 7. Cette approximation est illustrée à la figure 6, avec le modèle exact. Notez également que la taille de la grille pour le modèle oscillatoire est presque indépendante de la largeur de bande relative pour un petit bw. Il convient également de mentionner que, tant pour le modèle oscillatoire que pour le modèle de l’enveloppe, la résolution de grille maximale Δxmax est liée à la racine carrée de la fidélité en amplitude cible. Ces valeurs représentent la résolution de grille maximale requise pour respecter le code, sur la base du modèle phénoménologique.
(a) Le scénario le plus défavorable pour le traitement TFM oscillatoire se produit lorsque l’axe |
(b) Le scénario le plus défavorable pour l’enveloppe TFM se produit lorsque le profil d’amplitude le long de |
Figure 5 : Illustration de l’orientation du défaut par rapport à l’axe orthogonal de la grille pour le scénario le plus défavorable,
pour (a) la TFM oscillatoire et (b) l’enveloppe TFM.
Validation expérimentale
Le modèle proposé est validé avec les résultats empiriques de trois scénarios d’inspection TFM différents. Pour les trois configurations TFM, plusieurs SDH ont fait l’objet d’une acquisition à différentes résolutions de grille, et la fidélité en amplitude a été mesurée à l’aide de la méthode décrite précédemment. Les paramètres des trois scénarios d’utilisation sont indiqués dans le tableau 1. Le premier scénario repose sur un contact avec une sonde à haute fréquence (7,5 MHz), le second scénario sur des ondes transversales à une fréquence de sonde inférieure (5 MHz), et le troisième scénario sur des ondes transversales à une fréquence de sonde supérieure (10 MHz) avec un nombre d’éléments plus élevé. Dans tous les scénarios, les SDH sont situés à moins de 50 mm de la surface supérieure d’un bloc en acier non allié.
Tableau 1 : Paramètres des configurations TFM utilisées pour la validation expérimentale de la fidélité en amplitude
| Scénario | Paramètres de la sonde | Paramètres du sabot | Paramètres de la pièce | Mode TFM | |||||
|---|---|---|---|---|---|---|---|---|---|
|
Fréquence
[MHz] |
Nombre
[#] |
Pas
[mm] |
Vitesse de propagation
[m/s] |
Angle
[°] |
Hauteur
[mm] |
Vitesse de propagation
cp - cs [m/s] |
Diamètre du
SDH [mm] | ||
| 1 | 7,5 | 64 | 1,0 | s.o. | s.o. | 0 | 3240 - 5890 | 1 | L-L |
| 2 | 5 | 32 | 1,0 | 2330 | 36,1 | 11,0 | 3240 - 5890 | 0,5 | T-T |
| 3 | 10 | 64 | 0,5 | 2330 | 36,1 | 11,0 | 3240 - 5890 | 1 | T-T |
La figure 5 montre la fidélité en amplitude résultante pour la TFM oscillatoire standard (en haut) et pour l’enveloppe TFM (en bas). Chaque point gris représente une combinaison différente de scénario d’utilisation, de SDH et de résolution de grille. La fidélité en amplitude estimée à l’aide du modèle gaussien présenté précédemment est représentée par une courbe noire continue. La ligne rouge pointillée représente la limite de conformité avec le code, soit 2 dB.
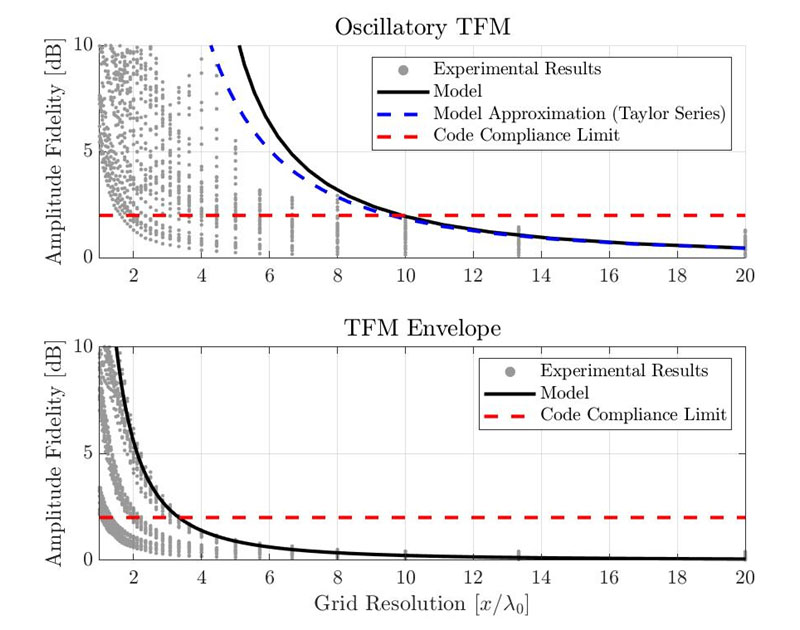
Figure 6 : Comparaison entre les mesures empiriques de la fidélité en amplitude et les résultats du modèle gaussien proposé
pour la TFM oscillatoire standard (en haut) et pour l’enveloppe TFM (en bas)
Avec le modèle proposé, la résolution nécessaire pour respecter le code est λ0/9,9 pour la TFM oscillatoire et λ0/3,3 pour l’enveloppe TFM. Les résultats expérimentaux montrent que la résolution de grille minimale pour respecter le code est d’environ λ0/10 pour la TFM oscillatoire standard et de λ0/3,3 pour l’enveloppe TFM. Notez toutefois que ces valeurs ont été obtenues à partir du pire cas expérimental présenté. Certaines des valeurs de fidélité en amplitude mesurées sont inférieures à 2 dB, même avec une résolution de grille plus grossière. Par conséquent, le modèle proposé fournit des estimations de fidélité en amplitude d’une configuration TFM qui s’avèrent bonnes, quoique prudentes.
Conclusion
La fidélité en amplitude d’une configuration TFM est une mesure importante de la robustesse de l’imagerie par rapport à la résolution de la grille. Plus la grille est dense, plus la valeur de la fidélité en amplitude est basse. Les codes et les normes incluent désormais la méthode de focalisation en tout point comme nouvelle technique d’inspection et exigent que la fidélité en amplitude ne dépasse pas les 2 dB. Cet article a présenté comment on peut mesurer la fidélité en amplitude de façon empirique, et a proposé un modèle analytique simple pour estimer la fidélité en amplitude à partir des résultats obtenus pour une configuration TFM.
Un modèle analytique simple a été proposé, reposant sur le profil d’amplitude le long de l’axe principal de la propagation acoustique. Le modèle estime le profil d’amplitude comme une oscillation gaussienne modulée par la fonction cosinus. L’utilisation de ce profil pour estimer la fidélité en amplitude donne de bons résultats pour la TFM oscillatoire standard et pour l’enveloppe TFM. Les résultats empiriques ont montré la nécessité d’une résolution de grille allant jusqu’à λ0/10 ou λ0/3,3, respectivement, pour la TFM oscillatoire standard et l’enveloppe TFM. Le modèle analytique proposé estime la nécessité d’une résolution de grille de λ0/9,9 pour la TFM standard et de λ0/3,3 pour l’enveloppe TFM. Par conséquent, le modèle proposé pourrait être utilisé pour estimer la fidélité en amplitude d’une configuration TFM.
Pour en savoir plus sur les avantages de l’utilisation de l’enveloppe TFM dans le cadre d’une solution conforme au code, vous pouvez lire l’article technique suivant : Utilisation de la méthode d’inspection TFM et de la fonction de traitement d’enveloppe.
Bibliographie
[1] Comité de l'American Society of Mechanical Engineers (ASME), « ASME BPVC.V Article 4 Mandatory Appendix XI Full Matric Capture », 2019.
[2] ORALKAN, O., ERGUN, A. S., JOHNSON, J. A., KARAMAN, M., DEMIRCI, U., KAVIANI, K., LEE, T. H., et KHURI-YAKUB, B. T. « Capacitive Micromachined Ultrasonic Transducers: Next-Generation Arrays for Acoustic Imaging? », IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 49, n° 11, 2002, p. 1596-1610.
[3] THOMENIUS, K. E. « Evolution of Ultrasound Beamformers », Proceedings of the IEEE Ultrasonics Symposium, IEEE, San Antonio, TX, É.-U., 1996, p. 1615-1622.
[4] FREEMAN, S., LI, P. et O’DONNELL, M. « Retrospective Dynamic Transmit Focusing », p. 24.
[5] WILCOX, P. D. « Exploiting the Full Data Set from Ultrasonic Arrays by Post-Processing », AIP Conference Proceedings, AIP, Brunswick, Maine (É.-U.), 2006, p. 845-852.
[6] PORTZGEN, N., GISOLF, D. et BLACQUIERE, G. « Inverse Wave Field Extrapolation: A Different NDI Approach to Imaging Defects », IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, vol. 54, n° 1, 2007, p. 118-127.
[7] SHARPE, R. S. (éditeur). « Research Techniques in Nondestructive Testing », vol. 6, n° ..., Academic Press, Londres, 1982.
[8] HOLMES, C., DRINKWATER, B. W. et WILCOX, P. D. « Advanced Post-Processing for Scanned Ultrasonic Arrays: Application to Defect Detection and Classification in Non-Destructive Evaluation », Ultrasonics, vol. 48, n° 6-7, 2008, p. 636-642.
[9] HOLMES, C., DRINKWATER, B. W. et WILCOX, P. D. « Post-Processing of the Full Matrix of Ultrasonic Transmit–Receive Array Data for Non-Destructive Evaluation », NDT & E International, vol. 38, n° 8, 2005, p. 701-711.
[10] ISO, « ISO/DIS 23865 -FMC-TFM - General Use of TFM-FMC Technique », 2020.
[11] JOHNSON, P. « Code Compliant TFM Weld Inspection with Three Clicks » (pour la citation : « With a New Software Wizard, There’s No Sorcery but the Magic of the M2M Gekko Is Evident with Instant Code Compliance for Your TFM Weld Inspections »), 2019.
[12] Comité de l'American Society of Mechanical Engineers (ASME), « ASME BPVC.V Article 4 Nonmandatory Appendix F - Examination of Welds Using Full Matrix Capture », 2019.