常规探头的波前动态属性
Formazione del fronte d'onda
Mentre una sonda a singolo elemento può essere considerata come un pistone, un disco o piastra che sposta esercitando una compressione verso il materiale ispezionato, il fronte d'onda che genera può essere modellizzato matematicamente come la somma delle onde di numerosi fonti puntuali. Questo deriva dal principio di Huygens, formulato dal fisico olandese Christiaan Huygens nel XVII secolo, nel quale si afferma che ogni punto su un fronte d'onda che avanza può essere considerato come una fonte puntuale che genera una nuova onda sferica. Inoltre si afferma che il fronte d'onda unificato che ne risulta è dato dalla somma di tutte queste onde sferiche separate.
Diffusione del fascio
In linea di principio l'onda ultrasonora generata da una sonda si sposta in linea retta fino a quando incontra un limite materiale. Le conseguenze vengono riportate di seguito. Se la lunghezza del percorso ultrasonoro è superiore alla lunghezza del campo vicino, il fascio aumenta di diametro e diverge come il fascio di un proiettore. L'angolo di divergenza del fascio di una sonda può essere calcolato nel seguente modo:

In questa equazione è possibile constatare che la divergenza del fascio aumenta con delle basse frequenze e dei diametri ridotti. Un fascio con un ampio angolo di divergenza può causare, con la distanza, una diminuzione rapida dell'energia ultrasonora per l'unità della superficie e causare inoltre una considerevole diminuzione dell'energia ultrasonora di riflettori di ridotte dimensioni in applicazioni caratterizzate da lunghi percorsi ultrasonori. In alcuni casi, la risposta dell'eco può essere migliorata usando una frequenza maggiore o una sonda di diametro maggiore.
Attenuazione
Quando si sposta in un mezzo, il fronte d'onda organizzato generato da una sonda ad ultrasuoni comincia a degradarsi a causa di una trasmissione imperfetta dell'energia nella microstruttura dei materiali. Le vibrazioni meccaniche organizzate (onde sonore) si trasformano in vibrazioni meccaniche casuali (calore) fino a quando il fronte delle onde non è più rilevabile. Questo fenomeno è noto come attenuazione acustica.
La teoria matematica dell'attenuazione e della diffusione è complessa. La perdita di ampiezza dovuta all'attenuazione nell'ambito di un determinato percorso ultrasonoro sarà data dalla somma degli effetti di assorbimento, i quali aumentano linearmente in funzione della frequenza, e degli effetti di diffusione, i quali variano in tre zone in base al rapporto della dimensione dei limiti intergranulari o di altri diffusori in rapporto alla lunghezza d'onda. In tutti i casi, gli effetti di diffusione aumentano con la frequenza. Un dato materiale ad una determinata temperatura ed una specifica frequenza d'ispezione, presenta un coefficiente d'attenuazione specifico, generalmente espresso in Neper per centimetro (Np/cm). Quando questo coefficiente d'attenuazione è noto, le perdite per un dato percorso ultrasonoro possono essere calcolati in base all'equazione

In pratica, nelle applicazioni NDT ad ultrasuoni, i coefficienti di attenuazione vengono generalmente misurati e non calcolati. Le frequenze elevate vengono attenuate più rapidamente delle basse frequenze in tutti i materiali. Le basse frequenze d'ispezione vengono in genere usate per i materiali a coefficiente d'attenuazione elevato come le gomme e le plastiche a bassa densità.
Riflessione e trasmissione su un limite del piano perpendicolare
Quando un'onda ultrasonora che attraversa un materiale incontra il limite di un materiale differente perpendicolare alle onde, una parte dell'energia delle onde viene riflessa verso la fonte mentre l'altra parte prosegue il suo percorso. La percentuale di riflessione in rapporto alla trasmissione è legata all'impedenza acustica relativa dei due materiali, con un impedenza acustica definita a sua volta come la densità del materiale moltiplicata per la velocità di propagazione dell'onda ultrasonora. Il coefficiente di riflessione ad un limite piano, quindi la percentuale dell'energia sonora che viene riflessa verso la fonte, può essere calcolata nel seguente modo:

In questa equazione è possibile notare che quando i valori delle impedenze acustiche dei due materiali tendono ad approssimarsi, il coefficiente di riflessione diminuisce, mentre quando i valori delle impedenze acustiche tendono a discostarsi, il coefficiente di riflessione aumenta. In teoria la riflessione dei materiali con la stessa impedenza acustica sul limite tra due materiali è nulla, mentre quella di materiali d'impedenza acustica molto diversa, come nell'interfaccia tra acciaio ed aria, il coefficiente di riflessione si avvicina al 100%.
Rifrazione e modalità di conversione ai limiti non perpendicolari
Quando un'onda ultrasonora che attraversa un materiale incontra il limite di un altro materiale ad un angolo differente da zero, una parte dell'energia delle onde sarà riflessa con un angolo equivalente all'angolo d'incidenza. Contemporaneamente la parte dell'energia trasmessa nel secondo materiale sarà rifratta in base alla legge di Snell, la quale è stata ricavata in maniera indipendente da almeno due matematici del XVII secolo. La legge di Snell riguarda i seni dell'angolo incidente e dell'angolo di rifrazione in funzione della velocità di propagazione delle onde ultrasonore in ogni materiale, come illustrato nella seguente figura.
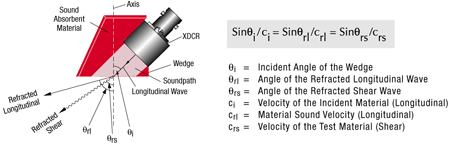
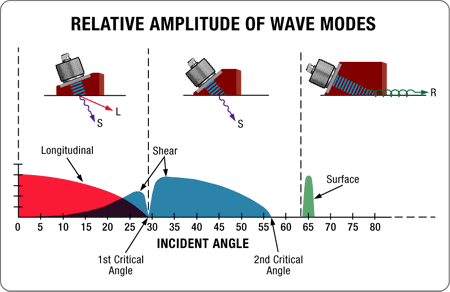
Se la velocità di propagazione dell'onda ultrasonora nel secondo materiale è maggiore rispetto al primo materiale, questa flessione si accompagna a un cambiamento della modalità al di sopra di alcuni angoli, in genere della modalità dell'onda longitudinale alla modalità dell'onda trasversale. Si tratta dei fondamenti delle tecniche d'ispezione a fasci angolari in genere adottate. Quando l'angolo d'incidenza nel primo materiale (lento, come lo zoccolo o l'acqua) aumenta, anche l'angolo dell'onda di rifrazione longitudinale nel secondo materiale (veloce, come il metallo) aumenta. Quando l'onda di rifrazione longitudinale raggiunge i 90 gradi, una parte progressivamente maggiore delle onde viene convertita in onde trasversali a bassa velocità rifratta con l'angolo previsto dalla legge di Snell. Con degli angoli d'incidenza maggiori rispetto a quelli in grado di creare onde di rifrazione longitudinali di 90 gradi, l'onda di rifrazione sarebbe completamente in modalità trasversale. Un angolo d'incidenza ancora superiore provocherà in teoria la rifrazione di 90 gradi di un onda trasversale, a tal punto viene generata un'onda superficiale nel secondo materiale. Il diagramma sottostante illustra questo effetto su una sonda a fascio angolare tipica accoppiata sull'acciaio.