Autori: Nicolas Badeau, Guillaume Painchaud-April, and Chi-Hang Kwan
Sintesi
La tecnica di ispezione con metodo a focalizzazione è adesso inclusa in norme e standard che regolamentano i controlli non distruttivi (BDT), come la norma ASME Sezione V. Un importante parametro specificato in queste norme per la pianificazione della scansione TFM è rappresentato dalla corrispondenza dell'ampiezza. È definita come la variazione di ampiezza ottenuta per uno specifico riflettore, dovuta alla risoluzione finita della griglia dell'immagine. La tipica soglia della corrispondenza dell'ampiezza in queste norme prevede un valore massimo di 2 GB. Sebbene dalle norme siano consigliati metodi sperimentali per misurare la corrispondenza dell'ampiezza di una determinata configurazione, in questo articolo viene proposto un metodo analitico semplice e conservativo. L'uso dell'involucro TFM viene anche considerato nella stima della corrispondenza dell'ampiezza, visto che permette l'utilizzo di una griglia TFM meno densa, in modo che il valore della corrispondenza dell'ampiezza non superi la tolleranza definita. Per una standard imaging TFM, i risultati empirici hanno mostrato che, per ottenere una corrispondenza dell'ampiezza inferiore a 2 dB, è richiesta una risoluzione della griglia di circa λ0/10 . Per l'imaging TFM con l'involucro, i risultati empirici hanno mostrato la necessità di avere una risoluzione della griglia di λ0/3,3 per assicurare una conformità alla norma.
Introduzione
Il metodo di focalizzazione totale (TFM) è una nuova tecnica accettata per i controlli non distruttivi (NDT) delle componenti. Gli standard e le norme, come l'ASME V [1], hanno integrato l'acquisizione completa della matrice (FMC) e il metodo di focalizzazione totale (TFM) in qualità di supplementare tecnica di ispezione a ultrasuoni phased array. Sebbene l'FMC/TFM è una tecnica relativamente nuova nel settore NDT, è stata usata per alcune volte nelle applicazioni mediche come standard preferenziale nell'imaging a ultrasuoni in campo medico [2–4]. Infatti le maggior parte delle tecniche di imaging a ultrasuoni in campo medico sono in genere confrontate con l'imaging TFM.
Sebbene esistono alcune tecniche simili all'FMC/TFM (Es: VTFM [5], IWEX [6] e SAFT [7]), l'algoritmo più comunemente usato è quello dell'elaborazione ritardo-somma [2–4,8,9]. La tecnica FMC/TFM consiste di uno schema di acquisizione (FMC), il quale si basa sull'acquisizione del segnale da tutte le combinazioni degli elementi del trasmettitore-ricevitore, oltre a uno schema della somma (TFM), il quale calcola il risultato del fascio a ultrasuoni focalizzato in diversi punti in un'area di interesse. L'area di interesse TFM fa spesso riferimento a una griglia cartesiana. Inoltre con pixel si fa riferimento alle singole intersezioni della griglia alle quali si applica la focalizzazione acustica Il metodo di focalizzazione è simile all'imaging a ultrasuoni phased array standard, eccetto per il fatto che i fasci sono formati in post-elaborazione mediante i dati memorizzati nella matrice FMC dei dati. L'elaborazione ritardo-somma post-acquisizione presuppone la linearità delle principali onde acustiche trovate nelle tipiche applicazioni NDT.
La tecnica FMC/TFM può essere vista come naturale evoluzione della convenzionale tecnica phased array. Tuttavia devono essere considerati dei nuovi parametri di configurazione a causa delle differenze nella rappresentazione dei dati in confronto ai convenzionali controlli a ultrasuoni phased array (PAUT). Uno di questi è la corrispondenza dell'ampiezza (AF) di una griglia TFM. AF è definita come la variazione dell'ampiezza massima di un'indicazione causata dalla risoluzione della griglia TFM {Δx,Δz}. Per il resto di questo studio viene considerato l'uso di un'uniforme griglia cartesiana (es: [Δx=Δz]). La corrispondenza dell'ampiezza può essere formalmente espressa come:
![(Eq.1) AF(Δx)≡-20 log〖(A_(sampled max) (Δx))/A_(true max) 〗 [dB],](https://industrial.evidentscientific.com.cn/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_01.jpg?rev=43A1)
dove Asampled max rappresenta l'ampiezza massima di un parametro di interesse basata su un finito campionamento della griglia, mentre Atrue max rappresenta il massimo dello stesso parametro d'interesse basato su un'infinita risoluzione della griglia. Il limite al quale la dimensione della griglia diventa zero nei due assi per Asampled max (Δx) definisce Atrue max e la relativa corrispondenza dell'ampiezza diventa 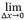 AF(Δx)=0. L'Equazione 1 fornisce una definizione formale per calcolare la corrispondenza dell'ampiezza in relazione alla risoluzione della griglia. Tuttavia, in pratica, il massimo reale Atrue max del segnale principale può essere stimato attraverso il sovracampionamento dell'immagine dell'ampiezza TFM e l'interpolazione
AF(Δx)=0. L'Equazione 1 fornisce una definizione formale per calcolare la corrispondenza dell'ampiezza in relazione alla risoluzione della griglia. Tuttavia, in pratica, il massimo reale Atrue max del segnale principale può essere stimato attraverso il sovracampionamento dell'immagine dell'ampiezza TFM e l'interpolazione
![(Eq.2) (AF) ̂(Δx)=-20 log〖(A_(sampled max) (Δx))/A ̂_(true max) 〗 [dB],](https://industrial.evidentscientific.com.cn/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_02.jpg?rev=43A1)
dove  true max può essere un elemento di stima di Atrue max.
true max può essere un elemento di stima di Atrue max.
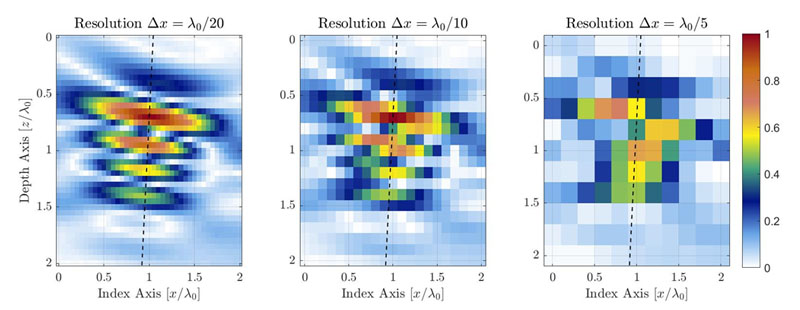
Figura 1. Illustrazione della degradazione della qualità dell'immagine TFM attraverso la diminuzione della risoluzione della griglia TFM. La linea tratteggiata rappresenta l'asse principale della propagazione acustica.
Per un'identica area d'interesse, una risoluzione della griglia inferiore avrà un numero di pixel inferiore. La Figura 1 mostra delle tipiche immagini TFM dello stesso SDH (side-drilled hole, foro laterale) per diversi valori della risoluzione della griglia. La risoluzione della griglia è definita come frazione della lunghezza d'onda della frequenza centrale della sonda λ0= c/f0, dove c è la velocità acustica nella componente e f0 è la frequenza centrale della sonda.
Gli standard e le norme prevedono adesso per la corrispondenza dell'ampiezza il requisito di non superare i 2 dB [1,10]. Questo requisito deriva dal compromesso applicativo tra qualità dell'immagine sufficiente per assicurare una corretta analisi NDT e la produttività d'ispezione, la quale è influenzata fortemente dalla densità della griglia TFM su una determinata area di interesse. Notare che l'equilibrio tra qualità dell'immagine TFM e produttività dell'ispezione è particolarmente importante per i dispositivi portatili autonomi che non possiedono un'elevata potenza di elaborazione. Si prevede che questa problematica non sarà più esistente prossimamente, visto che l'hardware integrato migliora in efficienza e la funzionalità di capacità di calcolo in remoto diventa largamente disponibile.
Sebbene siano stati proposti alcuni metodi empirici [10–12], in genere richiedono dei calcoli estensivi. Inoltre i risultati ottenuti non sono rappresentativi dell'ampiezza reale causata dalla risoluzione della griglia. Questa criticità sarà spiegata nella seguente sezione. Questo articolo tecnico presenta un metodo per stimare con precisione la corrispondenza dell'ampiezza di una configurazione TFM, in modo da aiutare un tecnico NDT a eseguire un'ispezione TFM produttiva e conforme alle norme.
Questo articolo è suddiviso nel seguente modo: Innanzitutto viene riportata una spiegazione completa del problema che i tecnici devono affrontare. In seguito viene descritto un metodo per misurare empiricamente la corrispondenza dell'ampiezza di una configurazione TFM. Nella sezione successiva viene proposto un modello analitico per stimare la corrispondenza dell'ampiezza. Il modello proposto viene in seguito confrontato con delle misure empiriche su tre diverse situazioni applicative TFM. Infine viene riportata una breve conclusione con incluso il lavoro realizzato.
Problematica
Sebbene una griglia molto ristretta, ovvero densa, permetta una corrispondenza dell'ampiezza molto ridotta, gli attuali dispositivi elettronici, in grado di sviluppare calcoli delle immagini TFM, possiedono ancora dei limiti di calcolo. Una maggiore risoluzione della griglia su un'area di interesse implica un maggior numero di punti di focalizzazione da calcolare, diminuendo conseguentemente la produttività e la velocità di scansione meccanica. Il tecnico NDT deve essere in grado di scegliere una risoluzione della griglia ottimale per massimizzare la produttività dell'ispezione assicurando, allo stesso tempo, una conformità alle norme.
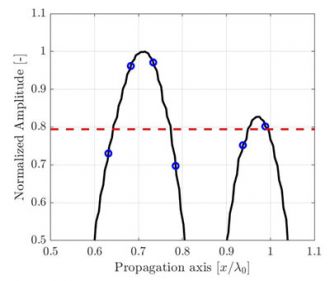
La corrispondenza dell'ampiezza può essere illustrata attraverso un semplice segnale unidimensionale in diversi periodi. Nell'esempio illustrato nella Figura 2 il segnale unidimensionale visualizzato è l'ampiezza dell'SDH riportato nella Figura 1 insieme all'asse di propagazione acustico, acquisito da un'immagine a alta risoluzione λ0/100. A fini esemplificativi viene riportata solo una parte zoomata in prossimità dell'ampiezza massima del segnale. Inoltre tre diverse risoluzioni (λ0/20, λ0/10 e λ0/5) sono identificate da cerchi blu su un riferimento interpolato a alta risoluzione (semplice curva nera).
(a) La risoluzione della griglia discreta è λ0/20 mentre la corrispondenza dell'ampiezza calcolata è AF = 0,27 dB.. |
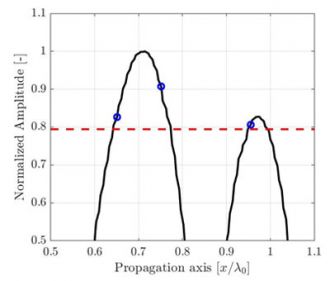
(b) La risoluzione della griglia discreta è λ0/10 mentre la corrispondenza dell'ampiezza calcolata è AF = 0,82 dB. |
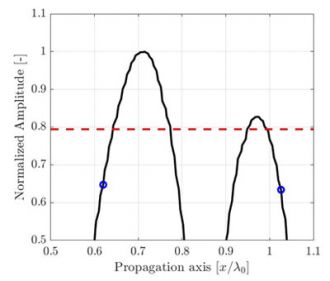
(c) La risoluzione della griglia discreta è λ0/5 mentre la corrispondenza dell'ampiezza calcolata è AF = 3,7 dB. |
Figura 2. Illustrazione dell'effetto del periodo di campionamento nell'ampiezza registrata insieme all'asse di propagazione rappresentato nella Fig. 1. Per facilitarne la visualizzazione viene riportato un riferimento del segnale interpolato a alta risoluzione (linea nera). La corrispondenza dell'ampiezza di 2 dB per la conformità alle norme è rappresentata da una linea tratteggiata rossa.
L'evidente conclusione è che una griglia più densa fornisce una migliore rappresentazione di un segnale continuo, come quantificato dal valore di corrispondenza dell'ampiezza attraverso l'Equazione 1, tuttavia continua a esistere il problema di ottimizzazione: Qual è la dimensione massima della griglia (Δxmax ) che garantisce, per tutte le possibili posizioni della griglia un'immagine TFM, una corrispondenza dell'ampiezza  equivalente a un valore target AFtarget? Oppure
equivalente a un valore target AFtarget? Oppure
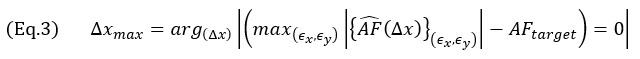
Da questa asserzione sul problema è chiaro come tutte le traslazioni della griglia, identificate dagli spostamenti (ϵx,ϵy), devono essere prese in considerazione per ottenere l' massimo per una dimensione fissa della cellula (Δx). Con questo sono stati trattati tutti i possibili casi di spostamenti della griglia per calcolare l'immagine TFM.
massimo per una dimensione fissa della cellula (Δx). Con questo sono stati trattati tutti i possibili casi di spostamenti della griglia per calcolare l'immagine TFM.
Nella seguente sezione viene riportata un'illustrazione del principio di misura per la serie di valori della corrispondenza dell'ampiezza prodotte da diversi spostamenti della griglia { (Δx)}(ϵx,ϵy).
(Δx)}(ϵx,ϵy).
Misura empirica della corrispondenza dell'ampiezza
Prima di presentare come la corrispondenza dell'ampiezza può essere stimata mediante un semplice modello analitico, risulta di primaria importanza definire come misurarla sperimentalmente nel caso di un'immagine TFM. Sono diverse le tecniche descritte e proposte nell'industria NDT [10–12], tuttavia alcune di esse non quantificano in modo esaustivo la corrispondenza dell'ampiezza. La misura empirica della corrispondenza dell'ampiezza può diventare rapidamente una gravosa acquisizione per il tecnico NDT che richiede il calcolo di numerose immagini TFM da diverse e precise posizioni della griglia TFM.
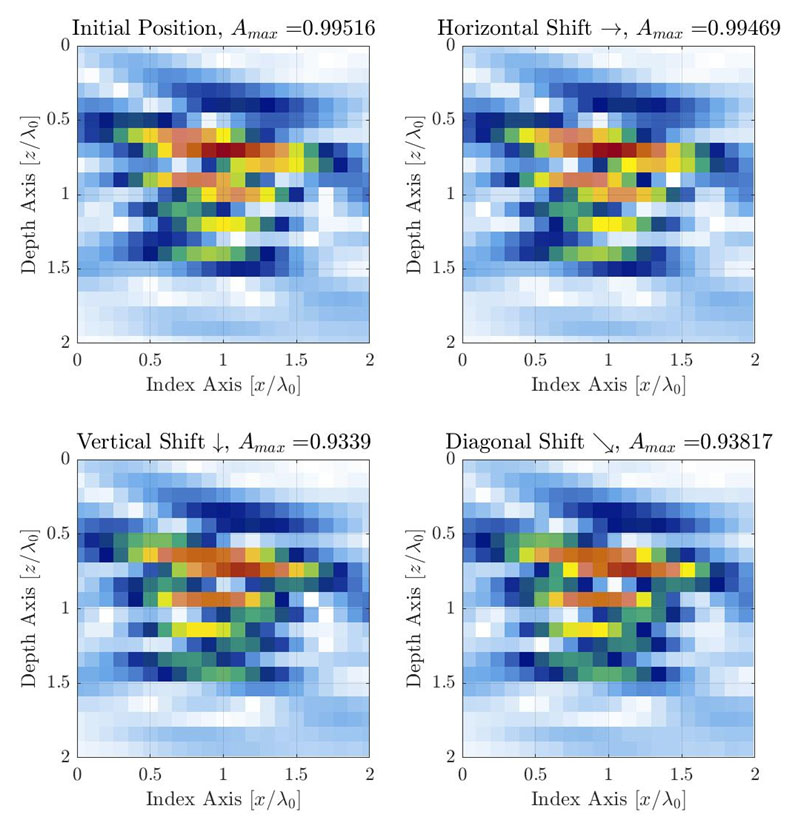
Figura 3 Illustrazione della variazione AF causata dalla discreta risoluzione della griglia visto che la griglia è spostata in 3 diverse direzioni. La risoluzione della griglia è definita come Δx=Δy=λ0/10. La griglia è traslata di un quarto della cella della griglia a destra (ϵx=λ0/40,ϵy=0) (in alto a destra), in basso (ϵx=0,ϵy=λ0/40) (in basso a sinistra) e diagonalmente (ϵx=λ0/40,ϵy=λ0/40) (in basso a destra).
Per le tipiche applicazioni TFM, viene usato un SDH come difetto di riferimento per la calibratura dell'ampiezza e la misura della corrispondenza dell'ampiezza [1,10]. L'ampiezza osservata varia principalmente lungo l'asse di propagazione acustica, la quale è una funzione della sonda, dello zoccolo e della posizione target nell'area di interesse (es: la posizione della griglia TFM relativa alla sonda). Nel caso illustrato nella Figura 1 il principale asse di propagazione è quasi verticale. Tuttavia, per un generico metodo di misura, l'asse di propagazione sarà diverso in funzione della posizione nell'area di interesse. Per un'immagine TFM la griglia di campionamento deve essere spostata in tutte le direzioni per acquisire la variazione dell'ampiezza reale causata dalla griglia discreta. Questo processo è illustrato di seguito con lo stesso esempio della Figura 1 (al centro), il quale ha una risoluzione della griglia di λ0/10.
Si consiglia di spostare la griglia di una frazione della risoluzione della griglia per verificarla (es: circa un dodicesimo della risoluzione) in ogni direzione per le volte necessarie per ottenere la sovrapposizione della griglia. Questo significa che per coprire uno scarto di una risoluzione della griglia nelle due direzioni ortogonali, è necessario un totale di 202 = 400 passi di traslazione, nel caso in cui si utilizzi il consigliato passo della griglia di un dodicesimo della risoluzione. L'ampiezza massima è registrata per ogni scarto della griglia e sono usati i valori registrati massimo e minimo per ottenere la corrispondenza dell'ampiezza mediante l'Equazione 2. Nel caos presentato nella Figura 3, la risoluzione della griglia è λ0/10 e la corrispondenza dell'ampiezza misurata è pari a 0,88 dB. Valutando il numero di spostamenti necessari, questo processo manuale risulterebbe difficoltoso e esigente in termini di tempo per il tecnico NDT. Inoltre si traduce in un totale di 400 immagini TFM che devono essere calcolati per misurare la corrispondenza dell'ampiezza di una singola risoluzione della griglia.
È utile menzionare che usando lo spostamento software della posizione della griglia TFM relativo alla sonda invece dello spostamento della sonda relativo alla parte, come proposto nella norma ASME Sezione V [12], diverse immagini TFM possono essere generate mediante un singolo dataset FMC. Un altro vantaggio di questo approccio è la capacità di accedere alla componente verticale della griglia. Infatti la sonda e lo zoccolo non possono essere spostati meccanicamente in relazione all'SDH selezionato lungo l'asse della profondità.
Alcuni dispositivi NDT forniscono prontamente degli strumenti semiautomatizzati che traslano la griglia TFM, registrano l'ampiezza massima nell'area di interesse e infine calcolano la risultante corrispondenza dell'ampiezza [11]. Tuttavia, questi strumenti in genere traslano la griglia solamente nella direzione orizzontale e, di conseguenza, sottostimano la corrispondenza dell'ampiezza. Per confronto, se la griglia è spostata solamente lungo l'asse orizzontale (es: come illustrato nella Figura 3), la corrispondenza dell'ampiezza misurata è di 0,06 dB. Questo valore è 15 volte inferiore rispetto alla corrispondenza dell'ampiezza misurata quando si considera l'asse verticale.
Un modello fenomenologico per la stima della corrispondenza dell'ampiezza
Questa sezione tratta un semplice modello analitico basato sull'osservazione empirica. Il modello fenomenologico considera il comportamento del segnale lungo il principale asse di propagazione, il quale si suppone che contenga la maggior parte delle fluttuazioni dell'ampiezza e, pertanto, risulta il più sensibile per la risoluzione della griglia. La Figura 4 mostra il profilo empirico di un'immagine TFM risultante si un SDH lungo il principale asse di propagazione (blu) e lungo l'asse del waist del fascio (rosso). L'origine dell'asse è posizionata nell'apparente posizione dell'ampiezza massima della rappresentazione dell'involucro. Questo spiega il ridotto scarto lungo l'asse  per la rappresentazione oscillatoria. Sono provvisti i profili per lo standard TFM oscillatorio e per l'involucro del TFM.
per la rappresentazione oscillatoria. Sono provvisti i profili per lo standard TFM oscillatorio e per l'involucro del TFM.
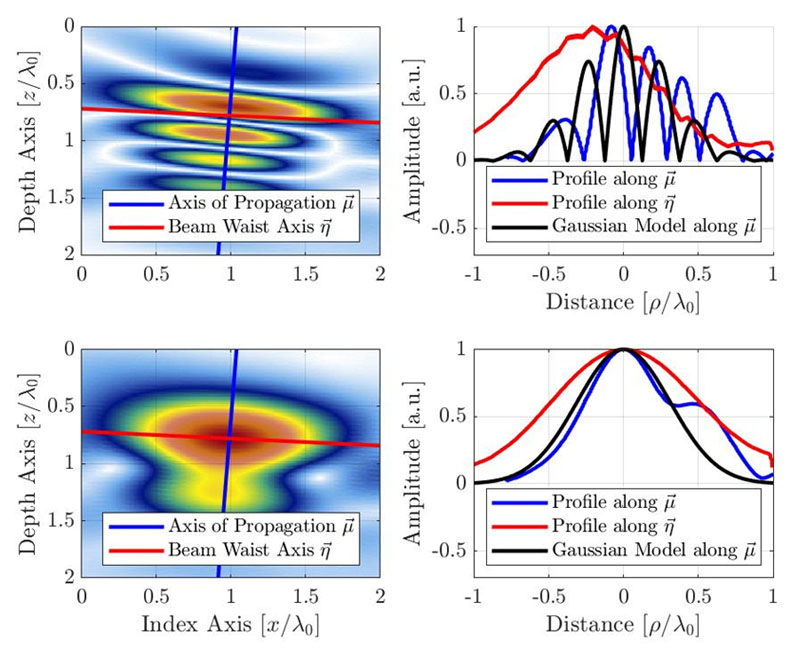
Figura 4. Immagine TFM (in alto: oscillatorio; in basso: involucro) con il profilo del segnale lungo l'asse di propagazione acustico e l'asse del waist del fascio. Il modello gaussiano proposto è inoltre illustrato per le immagini TFM oscillatorie e dell'involucro. Notare che l'apparente lunghezza d'onda è dimezzata a causa della natura dell'impulso eco relativa alla formazione del fascio TFM.
Come riportato precedentemente, l'asse con una maggiore variazione dell'ampiezza si suppone sia lungo l'asse principale della propagazione acustica. Pertanto il modello mira a riprodurre la variazione dell'ampiezza in questa direzione. Il segnale del modello è un gaussiano modulato con il coseno
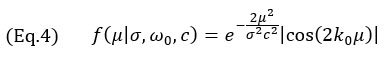
dove k0=ω0/c è il numero di onde nella frequenza angolare centrale ω0 della sonda, σ è il parametro della larghezza dipendente dalla frequenza centrale e la relativa larghezza di banda bw. Il parametro della larghezza σ è calcolato usando
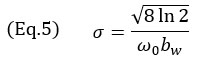
Per una tipica sonda phased array NDT, la relativa larghezza di banda è circa il 60% del valore di riferimento, pertanto nel modello viene usato un valore bw=0,6. Questo, a sua volta, rende l'involucro gaussiano più grande di una singola oscillazione del coseno. È utile menzionare che la frequenza centrale del termine coseno nell'Equazione 3 è raddoppiata dalla frequenza centrale della sonda. Questo è dovuto alla natura dell'impulso-eco dell'imaging TFM (percorso in trasmissione e ricezione) e può essere osservato nella distanza tra oscillazioni nella Figura 4. Infatti la conversione tra il tempo e lo spazio è scritta come μ = tc/2. Inoltre spiega perché viene usato il fattore 2 come termine esponenziale dell'Equazione 3.
Per il modello oscillatorio dell'Equazione 4, visto che l'involucro gaussiano è molto maggiore di una singola oscillazione della funzione coseno, sono considerati solo i valori |μ|≤λ0/8, visto che valori maggiori producono una distorsione spaziale per la corrispondenza dell'ampiezza.
Per il modello dell'involucro TFM viene usato solo il termine gaussiano dell'Equazione 4, ottenendo la seguente equazione:
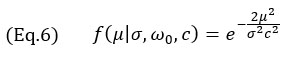
la quale è valida per qualunque risoluzione della griglia. Il profilo ottenuto con il modello delle Equazioni 3 e 7 illustrate nella Figura 4 insieme a profili sperimentali. Notare che le misure empiriche mostrano inoltre che il segnale dell'onda superficiale (l'eco "wrap around" tipico degli SDH) rimane indietro all'eco principale, un aspetto che è evidentemente assente nel modello proposto.
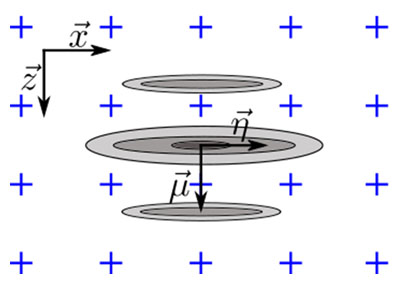
Deve essere considerata l'orientazione del difetto relativo agli assi ortogonali della griglia per definire la situazione più critica relativa alla corrispondenza dell'ampiezza con il modello. Come illustrato nella Figura 5a, la situazione più critica per il TFM oscillatorio si verifica quando l'asse principale della propagazione acustica  è parallelo a uno degli assi della griglia. Pertanto la corrispondenza dell'ampiezza deve essere calcolata come se l'ampiezza massima è centrata tra due punti della griglia lungo l'asse
è parallelo a uno degli assi della griglia. Pertanto la corrispondenza dell'ampiezza deve essere calcolata come se l'ampiezza massima è centrata tra due punti della griglia lungo l'asse 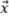 o
o 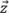 , ottenendo la seguente equazione:
, ottenendo la seguente equazione:
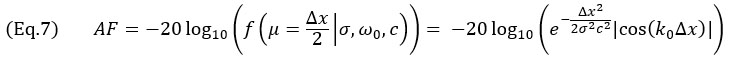
per Δx≤λ0/4. Per l'involucro TFM la situazione più critica si verifica quando il profilo dell'ampiezza è identico lungo l'asse principale di propagazione  e l'asse waist del fascio
e l'asse waist del fascio 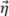 . Questa situazione, illustrata nella Figura 5b, corrisponde a quando l'SDH è rappresentato come cerchio e, pertanto, l'asse principale di propagazione
. Questa situazione, illustrata nella Figura 5b, corrisponde a quando l'SDH è rappresentato come cerchio e, pertanto, l'asse principale di propagazione  può avere qualsiasi orientazione. Come illustrato, la situazione più critica si verifica quando l'eco SDH è centrata tra quattro punti adiacenti. In questo caso la corrispondenza dell'ampiezza deve essere calcolato lungo la diagonale della griglia, ottenendo, in modo efficace, la seguente equazione:
può avere qualsiasi orientazione. Come illustrato, la situazione più critica si verifica quando l'eco SDH è centrata tra quattro punti adiacenti. In questo caso la corrispondenza dell'ampiezza deve essere calcolato lungo la diagonale della griglia, ottenendo, in modo efficace, la seguente equazione:
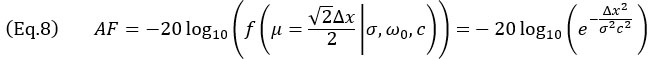
Nelle situazioni nelle quali il valore AF è piccolo, le quali sono le tipiche situazioni applicative NDT, una forma approssimativa per il valore di Δx in rapporto a AF può essere ottenuto per il modello oscillatorio dell'Equazione 7,

e il modello dell'involucro dell'Equazione 8,
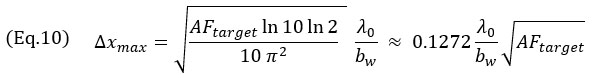
Queste espressioni descrivono la dipendenza della radice quadrata della dimensione della griglia nel valore AF in tutte le situazioni. L'Equazione 9 è stata ottenuta mediante l'approssimazione della serie di Taylor di secondo ordine dell'Equazione 7. Questa approssimazione è illustrata nella Figura 6 lungo il modello esatto. Inoltre notare che la dimensione della griglia per il modello di oscillazione è praticamente indipendente dalla relativa larghezza di banda per piccole bw. È utile menzionare che, per i modelli dell'oscillazione e dell'involucro, la risoluzione massima della griglia Δxmax è correlata alla radice quadrata della corrispondenza dell'ampiezza target. Questi valori rappresentano la risoluzione massima della griglia per la conformità della norma basata sul modello fenomenologico.
(a) La situazione più critica per l'TFM oscillatoria si verifica quando l'asse |
(b) La situazione più critica per l'involucro TFM si verifica quando il profilo dell'ampiezza lungo |
Figura 5. Illustrazione dell'orientazione del difetto relativa all'asse ortogonale della griglia per la situazione più critica, per (a) il TFM oscillatorio e (b) l'involucro del TFM.
Validazione sperimentale
Il modello proposto è validato con i risultati empirici in tre diverse situazioni applicative di ispezioni TFM. Per tutte e tre le configurazioni TFM, alcuni SDH sono stati rappresentati con immagini con diverse risoluzioni di griglie e la corrispondenza dell'ampiezza è stata misurata usando il metodo descritto precedentemente. I parametri delle tre situazioni applicative sono descritte nella Tabella 1. La prima situazione applicativa si riferisce al contatto con la sonda a alta frequenza (7,5 MHz), la seconda situazione applicativa utilizza onde trasversali a una frequenza inferiore (5 MHz) e la terza situazione applicativa utilizza le onde trasversali a una maggiore frequenza della sonda (10 MHz), oltre a un maggiore numero di elementi. In tutte le situazioni gli SDH sono posizionati a 50 mm dalla superficie superiore di un blocco di riferimento in acciaio al carbonio.
Tabella 1: Parametri delle configurazioni TFM usate per la validazione sperimentale della corrispondenza dell'ampiezza.
| Telaio | Parametri sonda | Parametri zoccolo | Parametri componenti | Modalità TFM | |||||
|---|---|---|---|---|---|---|---|---|---|
|
Frequenza
[MHz] |
Numero
[#] |
Passo
[mm] |
Velocità
[m/s] |
Angolo
[°] |
Altezza
[mm] |
Velocità
cp - cs [m/s] |
Diametro
SDH [mm] | ||
| 1 | 7,5 | 64 | 1,0 | n/a | n/a | 0 | 3240 - 5890 | 1 | L-L |
| 2 | 5 | 32 | 1,0 | 2330 | 36,1 | 11,0 | 3240 - 5890 | 0,5 | T-T |
| 3 | 10 | 64 | 0,5 | 2330 | 36,1 | 11,0 | 3240 - 5890 | 1 | T-T |
La Figura 5 mostra la risultante corrispondenza dell'ampiezza per il TFM oscillatorio standard (in alto) e per l'involucro TFM (in basso). Ogni singolo punto grigio rappresenta una diversa combinazione di situazione applicativa, SDH e risoluzione della griglia. La corrispondenza dell'ampiezza stimata usando il modello gaussiano presentato precedentemente è illustrato con una semplice curva nera. La linea tratteggiata rossa rappresenta il limite conforme alle norme di 2 dB.
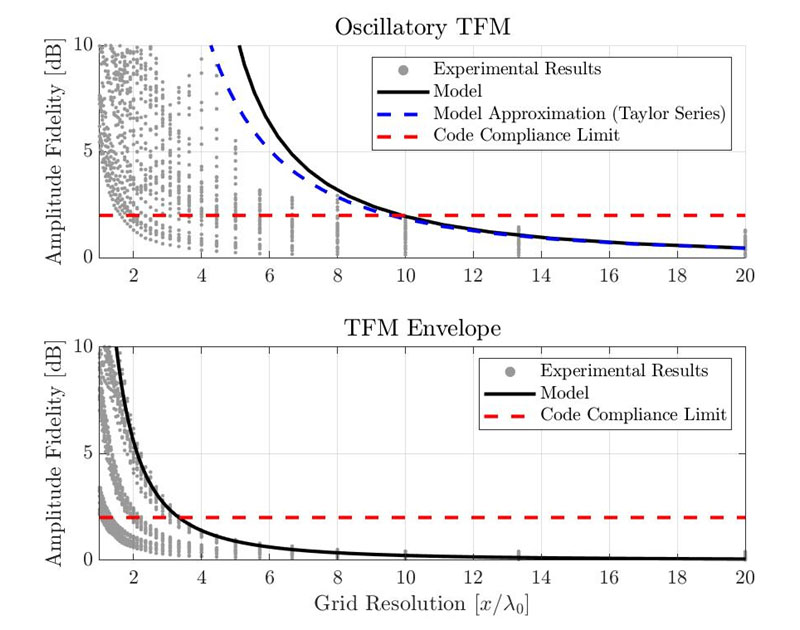
Figura 6. Confronto tra le misure della corrispondenza dell'ampiezza empirica e i risultati proposti del modello gaussiano per il TFM oscillatorio standard (in alto) e per l'involucro TFM (in basso).
Con il modello proposto la risoluzione necessaria per la conformità alle norme è λ0/9,9 per il TFM oscillatorio e λ0/3,3 per l'involucro TFM. I risultati sperimentali mostrano che la risoluzione minima della griglia per la conformità alla norma è di circa λ0/10 per il TFM oscillatorio standard e λ0/3,3 per l'involucro TFM. Tuttavia notare che questi valori sono stati acquisiti dalla situazione sperimentale più critica presentata. Alcuni dei valori misurati della corrispondenza dell'ampiezza sono inferiori a 2 dB, anche con una risoluzione della griglia minore. Pertanto il modello proposto fornisce delle stime valide ma conservative per la corrispondenza dell'ampiezza di una configurazione TFM.
Conclusione
La corrispondenza dell'ampiezza di una configurazione TFM è un'importante misura dell'efficacia dell'imaging in riferimento alla risoluzione della griglia. Maggiore è la densità della griglia e minore è il valore della corrispondenza dell'ampiezza. Le norme e gli standard adesso includono il metodo a focalizzazione totale come nuova tecnica di ispezione e richiedono un valore di 2 dB pari o inferiore della corrispondenza dell'ampiezza. Questo articolo tecnico presenta come la corrispondenza dell'ampiezza può essere misurato correttamente empiricamente e propone un semplice modello analitico per stimare la corrispondenza dell'ampiezza dei risultati per una configurazione TFM.
Un semplice modello analitico è stato proposto in base al profilo dell'ampiezza lungo l'asse principale della propagazione acustica. Il modello stima il profilo dell'ampiezza come oscillazione gaussiana modulata con coseno. Usando questo profilo per stimare la corrispondenza dell'ampiezza si ottengono dei validi risultati per il TFM oscillatorio standard e l'involucro TFM. I risultati empirici mostrano la necessità di una risoluzione della griglia massima di λ0/10 o λ0/3,3, rispettivamente, per il TFM oscillatorio standard e per l'involucro TFM. Il modello analitico proposto stima il bisogno per una risoluzione della griglia di λ0/9,9 per il TFM standard e λ0/3,3 per l'involucro TFM. Pertanto il modello proposto potrebbe essere usato per stimare la corrispondenza dell'ampiezza della configurazione TFM.
Per maggior informazioni sui vantaggi dell'uso dell'involucro TFM nell'ambito di una soluzione conforme alle norme, consultare l'articolo tecnico “Uso del Metodo di focalizzazione totale con la funzionalità dell'involucro.”
Bibliografia
[1] ASME Committee, 2019, “ASME BPVC.V Article 4 Mandatory Appendix XI Full Matric Capture.”
[2] Oralkan, O., Ergun, A. S., Johnson, J. A., Karaman, M., Demirci, U., Kaviani, K., Lee, T. H. e Khuri-Yakub, B. T., 2002, “Capacitive Micromachined Ultrasonic Transducers: Next-Generation Arrays for Acoustic Imaging?,” IEEE Trans. Ultrason., Ferroelect., Freq. Contr., 49(11), pp. 1596–1610.
[3] Thomenius, K. E., 1996, “Evolution of Ultrasound Beamformers,” 1996 IEEE Ultrasonics Symposium. Proceedings, IEEE, San Antonio, TX, USA, pp. 1615–1622.
[4] Freeman, S., Li, P. e O’Donnell, M., “Retrospective Dynamic Transmit Focusing,” p. 24.
[5] Wilcox, P. D., 2006, “Exploiting the Full Data Set from Ultrasonic Arrays by Post-Processing,” AIP Conference Proceedings, AIP, Brunswick, Maine (USA), pp. 845–852.
[6] Portzgen, N., Gisolf, D. e Blacquiere, G., 2007, “Inverse Wave Field Extrapolation: A Different NDI Approach to Imaging Defects,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 54(1), pp. 118–127.
[7] Sharpe, R. S., ed., 1982, Research Techniques in Nondestructive Testing. Vol. 6: ..., Acad. Press, London.
[8] Holmes, C., Drinkwater, B. W. e Wilcox, P. D., 2008, “Advanced Post-Processing for Scanned Ultrasonic Arrays: Application to Defect Detection and Classification in Non-Destructive Evaluation,” Ultrasonics, 48(6–7), pp. 636–642.
[9] Holmes, C., Drinkwater, B. W. e Wilcox, P. D., 2005, “Post-Processing of the Full Matrix of Ultrasonic Transmit–Receive Array Data for Non-Destructive Evaluation,” NDT & E International, 38(8), pp. 701–711.
[10] ISO, 2020, “ISO/DIS 23865 -FMC-TFM - General Use of TFM-FMC Technique.”
[11] Johnson, P., 2019, “With a New Software Wizard, There’s No Sorcery but the Magic of the M2M Gekko Is Evident with Instant Code Compliance for Your TFM Weld Inspections.,” Code Compliant TFM Weld Inspection with Three Clicks.
[12] ASME Committee, 2019, “ASME BPVC.V Article 4 Nonmandatory Appendix F - Examination of Welds Using Full Matrix Capture.”