常规探头的波前动态属性
波面形成
一振動子型探触子は試料の上で自ら励振して超音波を発生させます。探触子が生成する波は、非常に多数の波源から発生した波の合計として数学的にモデル化することも可能です。このことはホイヘンスの原理に由来します。この原理は17世紀にオランダ物理学者クリスチャン・ホイヘンスが最初に提唱したもので、進行する波面は新たな球面波(素元波)を発生する波源として考えられています。そしてその結果、生成される統一波面は個々の球面波の合計であるとしています。
指向角
原則として、探触子が生成する音波は物質の境界面に達するまで直進します。その後に何が発生するかについては下で論じます。仮にビーム路程が近距離音場限界距離より長い場合は、ビーム径も拡大し、スポット・ライトのビームのように広がります。フラット・タイプの探触子の指向角は以下のように計算されます:

この方程式から、指向角は低周波および小径になるほど大きくなるといえます。指向角が大きい場合、単位面積当たりの音エネルギーは距離と共に急速に減衰し、小反射体に対する感度が実質的に減少します。このため、長いビーム路程を伴うアプリケーションでエコー応答を改善するためには、高周波数、大径の双方もしくはどちらか一方を備えた探触子を使用することが必要です。
減衰
音が媒質を通過するにつれて、探触子により生成された超音波エネルギーは物質の結晶粒界で散乱し弱まります。さらに、超音波の機械的振動エネルギーは一部吸収され熱エネルギーに変化し弱まります。このプロセスは音の減衰として知られています。
減衰の数学的理論は複雑です。あるビーム路程上の減衰により生じる振幅損失は、吸収作用と散乱作用の合計です。吸収作用は周波数が高くなるほど直線的に増加し、散乱作用は波長と結晶粒界のサイズ比、または波長とその他の微小反射源のサイズ比に依存して変化します。全ての場合において、散乱作用は周波数と共に増大します。一定温度の一定物質を一定周波数で検査した場合、その物質にはネーパ比率(Np/cm)として一般的に知られる特有の減衰係数が存在します。この減衰係数が既知になると、あるビーム路程を超えた損失は次の方程式で計算できます:

実際の超音波非破壊検査では、減衰係数は通常計算ではなく測定により求めています。どのような媒質においても、高周波数の方が低周波数に比べて減衰速度が速くなります。そのため、低密度プラスチックやゴムのような減衰係数の高い物質の検査には、通常、低周波数が採用されています。
垂直境界面での反射と透過
ある媒質を伝播する音波が波方向と垂直の位置にある異なった媒質との境界面に達すると、超音波エネルギーの一部はそのまま反射し、一部は真っ直ぐに突き進みます。透過に対する反射率は二つの媒質の音響インピーダンス比に関係します。音響インピーダンスは媒質密度に音速を乗じた値として定義されます。垂直境界面での音圧反射率、即ち反射して音源に戻るエネルギーの割合は以下のように計算できます:

この方程式から、二つの媒質の音響インピーダンスの差が小さくなるに連れて、音圧反射率が減少します。逆に音響インピーダンスの差が大きくなるに連れて、音圧反射率は増加します。理論的には同じ音響インピーダンスをもった媒質間の境界面からの反射はゼロです。一方、例えば鉄と空気の境界面のように全く異なった音響インピーダンスの媒質の場合には、音圧反射率は、ほぼ100%になります。
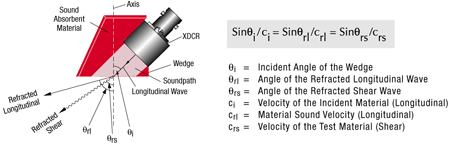
非垂直境界面での屈折とモード変換
ある物質を伝播する音波がゼロ以外の角度で異なる媒質の境界面に達すると、超音波エネルギーの一部は入射角と等しい角度で反射し進行します。同時に、第二の物質に透過した超音波エネルギーはスネルの法則に従って屈折します。スネルの法則は少なくとも二人の数学者が17世紀に別々に導き出した法則ですが、入射角と屈折角のサイン(正弦)比を各媒質の超音波の音速比と関連付けて説明しています。下図を参照して下さい。
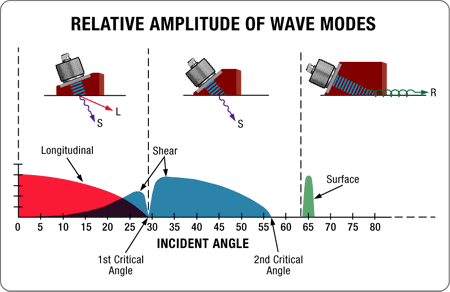
仮に二番目の媒質の方が一番目の媒質よりも音速が速い場合、上図で示すように、ある入射角では縦波から横波(せん断波)へのモード変換が発生します。この原理は最も幅広く使われている斜角検査法の基本となっています。一番目の媒質(ウエッジまたは水のように音速の遅い媒質)の入射角が増すのに伴い、二番目の媒質(金属のように音速の速い媒質)の縦波の屈折角は増します。縦波の屈折角が90°に近づくに連れて、超音波エネルギ―の大きな部分が音速の遅い横波に変換され、横波はスネルの法則により導き出された角度で屈折します。縦波の屈折角が90°より大きくなる場合、屈折波はモード変換した横波のみが存在する事になります。入射角が更に大きくなると結果的に横波が理論的には90°で屈折し、そこでは表面波が二番目の媒質の中に生成されます。下図はこの作用について、鋼中での典型的な斜角ビームを使って説明しています。