包络功能使全聚焦方式更出色

要約

本稿では、トータルフォーカシングメソッド（TFM）画像のエンベロープを算出する方法と、規格準拠ソリューションの一部としてTFMエンベロープを使用する利点について説明します。 TFMエンベロープは、2つの異なるTFM画像のノルムを計算することで取得されます。一方のTFM画像は、標準的な方法で取得されたフルマトリックスキャプチャ（FMC）を使って計算され、もう一方のTFM画像は、ヒルベルト変換されたFMCを使って計算されます。 その結果得られたTFMエンベロープ画像は、同一のグリッド分解能における標準振動TFM画像と比較して、振幅の変動に対する頑健性が高まるため、振幅を利用したサイジング法にさらに確固とした根拠を与えます。 標準振動TFMに関しては、TFMエンベロープに対してさらに粗いグリッド分解能を設定できます。その結果、合計計算量が減少し、最終的な取得速度が増大します。

はじめに

トータルフォーカシングメソッド（TFM）は、材料および構造の非破壊検査で近年利用が広まっている技法です。 現在、一部の標準および規格には、非破壊検査（NDT）用のフルマトリックスキャプチャ（FMC）およびTFMの項目が設けられています[1]、[2]。

OmniScan™ X3探傷器などの特定のNDT装置を使用することで、リアルタイムのTFMイメージングが可能になります。 FMCを使用するTFM技法は、以降で要約しますが、基本的な前提は、TFMが多数の振動子Aスキャン振幅値の合計に基づいていることです。 TFM画像は、データ元が振動子Aスキャンの音響波であるため、振動に基づきます。 一方、NDT用途で使われる特性評価方式は基本的に、振動動作が不必要な音響アーチファクトとみなされる振幅ベース技法です。 特性評価方式に振動動作を取り入れる通常のやり方は、振幅を修正することです。画像が真に正の値で表示されるようになります。 この技法によって、完全振動型に関しては画像解釈が容易になる場合があります。本稿では、信号エンベロープを使用することで、特性評価作業が改善され、標準の振動TFM画像に関して取得速度が実際に増大することを示します。

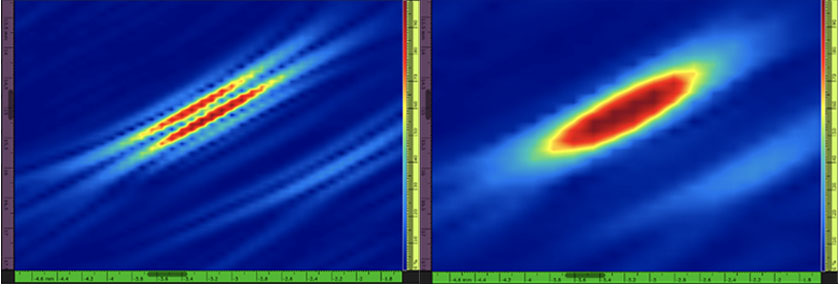
図1：左側：真に正の振幅値と信号振動（標準TFM）を有する横穴（SDH）のTFM画像の例。 グリッド分解能は0.08mm（λ/8.1）、最大振幅は108.7%です。 右側：同一のSDHにおけるTFMエンベロープ。 グリッド分解能は0.16mm（λ/4.0）、最大振幅は122.6%です。

このような振動TFM画像の使用には、いくつかの短所があります。 まず、規格に準拠するためには、TFMグリッド分解能（フレーム内における2つのピクセル間の距離）は約λ/8になる必要があります[1]-[3]。 本稿では、λはプローブの中心周波数とパーツの音響速度に関連する波長です。 グリッド分解能が小さいと、計算量が増大し、取得速度の低下に直結します。 振幅ベースの欠陥サイジング法に関係する頑健性も、振動TFMの影響を受けます。 実際、測定されるエコーの最大振幅は、取得した信号の位相オフセットによって大きく異なります。

これらの問題はすべて、TFMエンベロープを使用することで解決できます。TFMエンベロープによって、画像内の信号振動が除去され、より確実な最大振幅測定が可能になるためです（図1を参照）。 標準TFMと比較した場合、振幅の頑健性を同等にするために必要なグリッド分解能は低くて済むため（2つの隣接するピクセルの間隔が大きくなる）、TFMエンベロープの使用によって取得の効率は向上します。 例えば、分解能がλ/8の標準振動TFMと同じ振幅忠実度（2dB）を達成するには、TFMエンベロープでは約λ/4のグリッド分解能で十分です[3]。

本稿の目的は、TFMエンベロープを使用する利点をNDTのスペシャリストにお知らせすることです。 まず、FMC-TFM技法のまとめを行った後、TFMエンベロープの計算に関連する概念を簡単に説明します。 最後に、標準の振動式TFM画像と比較した場合の、規格準拠ソリューションの一部としてTFMエンベロープを使用する利点を示します。

FMC-TFM技法の要約

超音波フェイズドアレイの特徴は、検査対象のパーツの好きな位置に焦点を合わせられることです。 フェイズドアレイのフォーカス技法では、発信および受信の両方の遅延を使用し、目的位置で短いパルス信号の伝播時間を同期します。 検査対象内部の集束ゾーンでは、生成される音響ビームの全体的な幅が小さくなり、対応する検出分解能が飛躍的に増大します[4]-[12]。

TFMはこの機能をさらに発展させたものです。TFMはフェイズドアレイの集束機能とステアリング機能を使用して、検査対象のパーツ内部における関心領域（ROI）全体の各ポイントで集束ビームを生成します。高分解能集束データポイントのセットのみがオペレーターに示されます[13]–[16]。 多くの場合、関心領域はすべての集束目標における均一なデカルト格子で構成されます。 従来型の物理ビーム形成技法を使って、各グリッド位置でこのような集束を実現するには、各目的位置に到達するのに要する物理的な音響伝達時間が長いため、非常に時間がかかることは明白です。

NDT用途における通常の超音波は線形であるため、特定の開口部におけるすべての寄与振動子について、実際の音場の重ね合わせから得られる物理的なビーム形成の結果を、フルマトリックスキャプチャ（FMC）データセットに基づいた収集後プロセスによってエミュレートすることができます。 FMCデータセットを取り出すには、受信開口部を構成するすべての振動子からの信号を記録する必要があるのに対して、音響放出は、発信開口部を構成する個々の振動子によって生成されます。 つまり、FMCデータセットは、発信振動子と受信振動子のすべての組み合わせに対する多数の振動子Aスキャンによって形成されます。

従来型の集束型フェイズドアレイと同様に、特定の集束位置から集束された振幅を取得するには、次のことが必要になります。

• 開口部の発信振動子および受信振動子の全ペアについて、音響伝達が、選択された目標グリッド位置に合致する集束位置に到達し、受信振動子に戻るまでに要する伝播時間の計算
• 開口部の発信振動子および受信振動子の全ペアについて、発信から受信までの適切な総伝播時間に対応する振幅データポイントの選択
• 発信と受信の開口部におけるすべての寄与振動子にわたって、選択されたすべての振幅データポイントの合計
• 最初に選択したグリッド位置における、結果として得られた振幅合計値の配置

関心領域全体にわたるすべてのグリッド位置に対してこのステップを繰り返すと、発信と受信の両方において、すべての振幅値が集束ビームに対応する振幅マップが作成されます。 FMCデータを使用して、関心領域（TFMゾーン）全体にわたって、各位置に集束した振幅のマップを作成するこの方法をFMC-TFM技法といいます。

TFMエンベロープの計算方法

この項では、標準TFM用に取得した同じ振動子Aスキャン（FMC）を使用して、TFMエンベロープを計算する方法について説明します。 エンベロープは物理的な状態を表現する手段であって、単なる画像の平滑化アルゴリズムではないことにご注意ください。 TFM画像のエンベロープは、それを構成する個々のAスキャンが基になっています。 まず、その動作を図示すると、エンベロープの概念は、ガウス形パルス時系列を使用して示されます。 そのプロセスは、TFMフレーム全体の実証的Aスキャンに対しても適用されます。

信号a(t)は、取得信号に対応します。つまり、FMCを通して取得した振動子Aスキャンと同等のものであり、複雑な解析信号z(t)の実部になります。これを次のように書くことができます。

ここでa'(t)は解析信号の虚部に対応し、θ(t)は信号の瞬時位相です。 虚部は、ヒルベルト変換を使用して有効に計算されます[17]。 この信号エンベロープは、解析信号のノルムに対応します。これを次のように書くことができます。

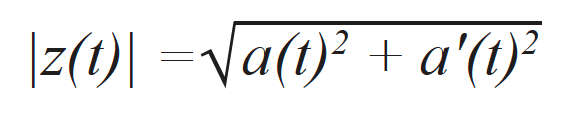
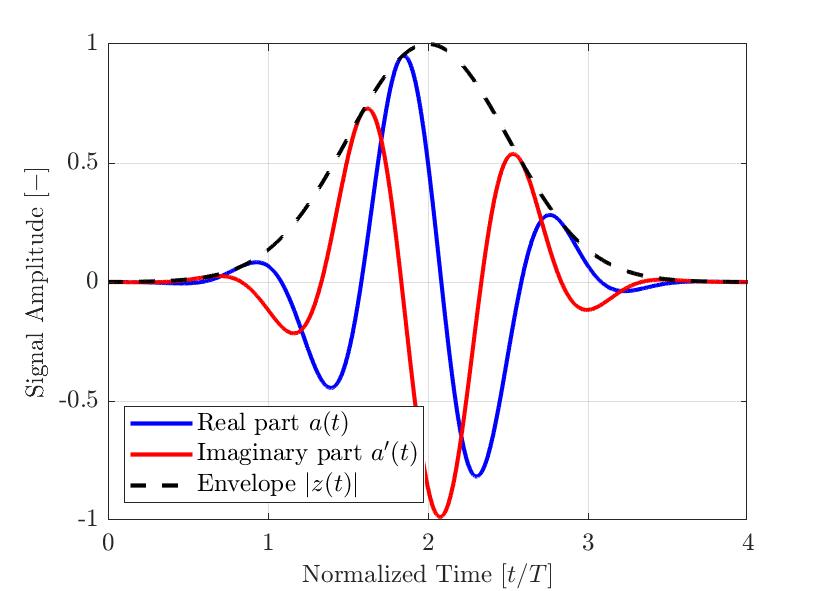
図2：NDT用途の典型的なガウス変調パルス 実部、虚部および算出エンベロープが示されています。 時間軸は、選択された中心周波数パルス周期を使って正規化されています。

図2は、シンプルなガウス変調パルスa(t)の例を示しています。 実際の信号a(t)は青色、それをヒルベルト変換した虚部a'(t)は赤色、その結果のエンベロープ|z(t)|は破線で描かれています。 上記の式で見られるとおり、信号エンベロープ|z(t)|は、信号の瞬時位相θ(t)の影響を受けません。 位相オフセットφの異なる信号は、同じエンベロープを持つことができます。 図3は、異なる位相オフセットφを持ついくつかのガウス変調パルスと、その結果のエンベロープを示しています。 信号エンベロープを使用した場合の信号の測定最大振幅は、解析信号の実成分の絶対値より頑健です。

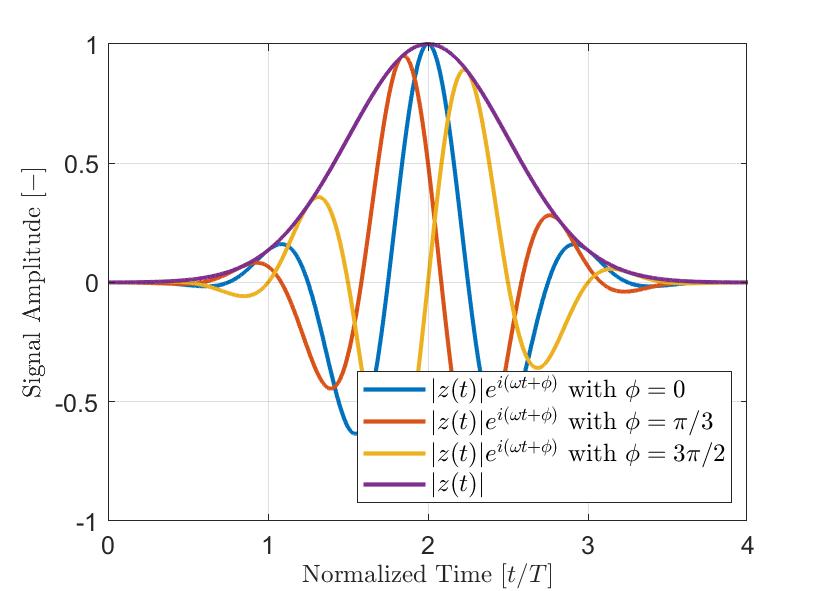
図3：異なる位相オフセットφを持つ典型的なガウス変調パルス(|z(t)|e^i(ωt+φ)) 信号のエンベロープ|z(t)|は、明らかに解析信号の瞬時位相の影響を受けません。

同じプロセスを使用して、実証的Aスキャンのエンベロープを取得することができます。 図4は、FMCを通して取得した典型的な振動子Aスキャンを示しています。一方、図5は同じAスキャン（青色）を、そのヒルベルト変換（赤色）および算出エンベロープ（破線）とともに示しています。 示されているすべての信号は、振幅エンベロープの最大値に正規化されます。

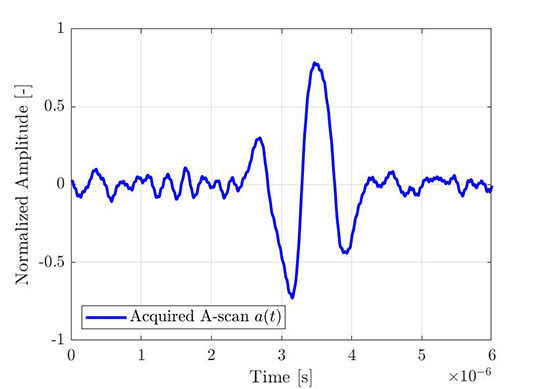図4：取得した振動子Aスキャンの一部（FMCにより取得）。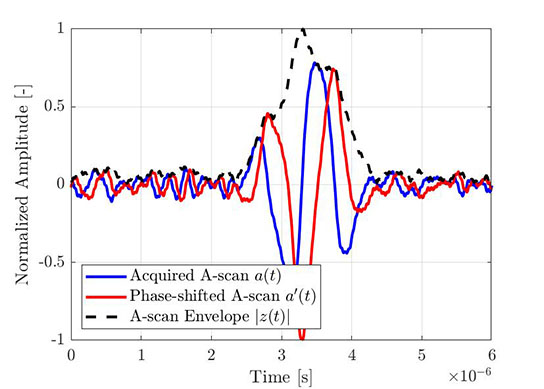

図5：同一の振動子Aスキャン、そのヒルベルト変換および算出エンベロープ。

TFMエンベロープの画像（個々のグリッドポイントインデックス(k,l)付き）は、それに寄与するすべてのAスキャンで得た解析信号を使って計算されます[15]。 これは実際には、標準FMCの取得データを使って計算された標準TFMフレームy(k,l)と、FMCデータのヒルベルト変換を使って計算されたTFMフレームx'(k,l)から成る解析TFM画像y(k,l)のノルムの計算結果です。 どちらの場合も、同じ遅延設定が使用されます。 次にTFMエンベロープは、次に示す式を使って計算されます。

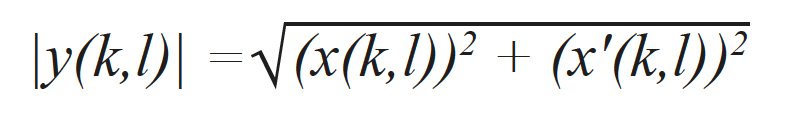
TFMエンベロープ画像は、2つのTFM画像を組み合わせた結果になります（図6を参照）。一方のTFM画像は、振動子Aスキャンの実成分の画像であり、もう一方のTFM画像は、振動子Aスキャンから算出された虚数成分の画像です。 このプロセスは、計算の負荷を増大し、NDT装置の取得速度を低下させます。次の項では、振幅精度への影響なしに必要なグリッド分解能を大幅に減少させることで、標準TFMの使用時よりも収集速度を増大できることを示します。

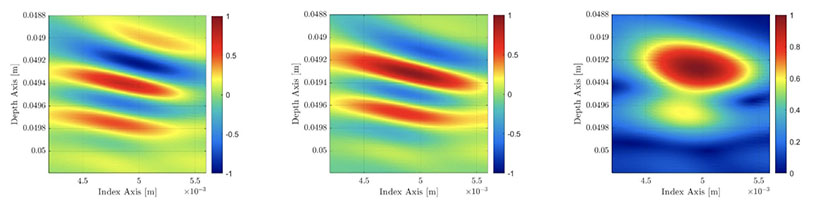
図6：左：標準TFMフレーム（絶対値ではない）。 中央：FMCのヒルベルト変換を使って計算されたTFMフレーム。 右：その結果のTFMエンベロープ画像。

TFMエンベロープを使用する利点

この項では、λ/9.3～λ/4.0のさまざまなグリッド分解能比を有するTFMフレームをいくつか比較し、各種の重要な検査メトリックをモニタすることで、TFMエンベロープの利点を示します。 その結果は、1mm径の横穴（SDH）を有する鋼鉄製ブロック上で、5L32-A31プローブとSA31-N55S-IHCウエッジを使用して得たものです（図7を参照）。 ウエッジと鋼鉄製ブロックの間にはカップリングゲル（Sonotech Ultragel II）を使用します。 データは、オリンパスのOmniScan™ X3探傷器を使用して取得します。 パルスエコー（T-T）音響経路が選択され、ゾーンサイズは（20mmx20mm）です。 パーツおよび選択した音響経路に関連した波長はλ=0.648mmです。 グリッド分解能は、波長の分数に関して記録されます。

図7：表1におけるTFM画像の取得で使用されるセットアップの画像。 青色長方形は関心領域全体（20mmx20mm）に対応し、赤色長方形は表1の画像に示されている関心領域（5mmx5mm）のズーム域に対応します。 5L32-A31プローブとSA31-N55S-IHCウエッジを使用しました。 鋼鉄製ブロックの厚さは40mmです。

表1は、標準TFMとTFMエンベロープの両方に関して、λ/9.3～λ/4.0の異なる4つのグリッド分解能値に対する結果のTFM画像を示します。 算出された振幅忠実度値[3]およびその結果の取得速度は、各TFM画像に示されています。

グリッド分解能	標準TFM	TFMエンベロープ
λ/9.3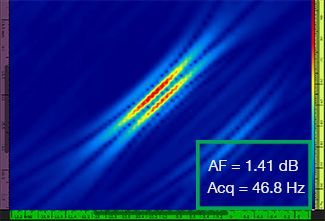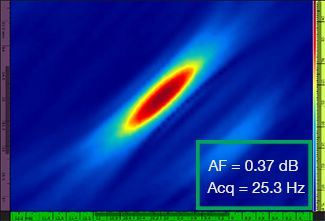
λ/8.1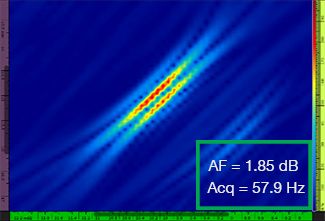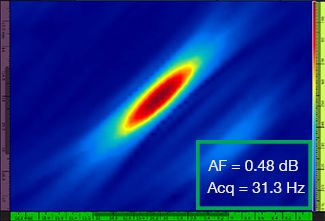
λ/5.9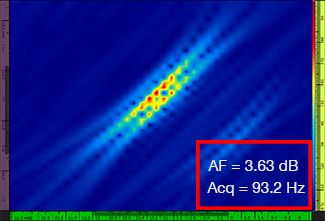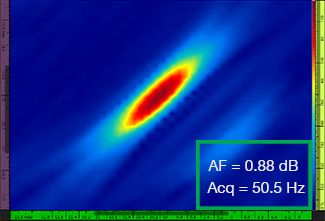
λ/4.0

新たに公表された規格[1,2]では、2dB以下の振幅忠実度値が必要です。 標準TFMを使用する場合は、最初の2つのグリッド分解能値（λ/9.3、λ/8.1）のみが規格準拠です。 TFMエンベロープを使用すると、規格準拠の振幅忠実度を維持しながら、グリッド分解能を粗く（λ/4.0）することができます。 次に、グリッドを粗くしたTFMエンベロープを使用すると、規格準拠の標準TFMで達成される最大取得速度（λ/8.1で57.9Hz）と比べて、約37%取得速度が増大します。

結論

TFM画像のエンベロープの計算方法を、シンプルな例を使って説明および図示しました。 信号のエンベロープは瞬時位相に依存しないため、振幅を利用したサイジング技法（6dBドロップ法など）において、より頑健性の高い根拠を提供することを説明しました。 信号エンベロープは、単に画像の平滑化ではないため、フィルターとみなすべきではありません。データ喪失が発生するおそれがあります。 さまざまなグリッド分解能値で、エンベロープを使った場合と使わなかった場合におけるTFM画像を比較することによって、TFM画像処理でエンベロープを使用する利点を示しました。 結果のTFMエンベロープを取得するには、2つのTFM画像を計算する必要がありますが、規格を準拠したまま、より粗いグリッド分解能を使用することで、処理の負荷をかなり軽減することができます。 振幅の変動に対してエンベロープの頑健性が高いためです。 その結果、振幅サイジングへの順応性を高めながら、標準TFMを使った同等の画像処理より速いペースで画像が取得されます。

参考資料

[1] ASME Committee, “ASME BPVC.V Article 4 Mandatory Appendix XI Full Matric Capture.” ASME, 2019.

[2] ASME Committee, “ASME BPVC.V Article 4 Nonmandatory Appendix F - Examination of Welds Using Full Matric Capture.” ASME, 2019.

[3] N. Badeau, A. Le Duff, and C.-H. Kwan, “Theoretical Model for Amplitude Fidelity Reading (submitted),” presented at the ASNT Research Symposium, 2020.

[4] A. C. Clay, S.-C. Wooh, L. Azar, and J.-Y. Wang, “Experimental Study of Phased Array Beam Steering Characteristics,” Journal of Nondestructive Evaluation, vol. 18, no. 2, p. 13, 1999.

[5] L. J. Bond, “Fundamentals of Ultrasonic Inspection,” ASM Handbook, vol. 17, no. Nondestructive Evaluation of Material, pp. 155–168, 2018.

[6] S.-J. Song, H. J. Shin, and Y. H. Jang, “Development of an ultra sonic phased array system for nondestructive tests of nuclear power plant components,” Nuclear Engineering and Design, vol. 214, no. 1–2, pp. 151–161, May 2002, doi: 10.1016/S0029-5493(02)00024-9.

[7] S. Mahaut, O. Roy, C. Beroni, and B. Rotter, “Development of phased array techniques to improve characterization of defect located in a component of complex geometry,” Ultrasonics, vol. 40, no. 1–8, pp. 165–169, May 2002, doi: 10.1016/S0041-624X(02)00131-2.

[8] S. C. Mondal, P. D. Wilcox, and B. W. Drinkwater, “Design of Two-Dimensional Ultrasonic Phased Array Transducers,” Journal of Pressure Vessel Technology, vol. 127, no. 3, pp. 336–344, Aug. 2005, doi: 10.1115/1.1991873.

[9] S.-C. Wooh and Y. Shi, “Influence of phased array element size on beam steering behavior,” Ultrasonics, vol. 36, no. 6, pp. 737–749, Apr. 1998, doi: 10.1016/S0041-624X(97)00164-9.

[10] Joon-Hyun Lee and Sang-Woo Choi, “A parametric study of ultrasonic beam profiles for a linear phased array transducer,” IEEE Trans. Ultrason., Ferroelect., Freq. Contr., vol. 47, no. 3, pp. 644–650, May 2000, doi: 10.1109/58.842052.

[11] R. Ahmad, T. Kundu, and D. Placko, “Modeling of phased array transducers,” The Journal of the Acoustical Society of America, vol. 117, no. 4, pp. 1762-1776, Apr. 2005, doi: 10.1121/1.1835506.

[12] B. W. Drinkwater and P. D. Wilcox, “Ultrasonic arrays for non-destructive evaluation: A review,” NDT & E International, vol. 39, no. 7, pp. 525–541, Oct. 2006, doi: 10.1016/j.ndteint.2006.03.006.

[13] P. D. Wilcox, “Exploiting the Full Data Set from Ultrasonic Arrays by Post-Processing,” in AIP Conference Proceedings, Brunswick, Maine (USA), 2006, vol. 820, pp. 845–852, doi: 10.1063/1.2184614.

[14] J. Zhang, B. W. Drinkwater, and P. D. Wilcox, “Effects of array transducer inconsistencies on total focusing method imaging performance,” NDT & E International, vol. 44, no. 4, pp. 361–368, Jul. 2011, doi: 10.1016/j.ndteint.2011.03.001.

[15] C. Holmes, B. W. Drinkwater, and P. D. Wilcox, “Advanced post-processing for scanned ultrasonic arrays: Application to defect detection and classification in non-destructive evaluation,” Ultrasonics, vol. 48, no. 6–7, pp. 636–642, Nov. 2008, doi: 10.1016/j.ultras.2008.07.019.

[16] C. Holmes, B. W. Drinkwater, and P. D. Wilcox, “Post-processing of the full matrix of ultrasonic transmit–receive array data for non-destructive evaluation,” NDT & E International, vol. 38, no. 8, pp. 701–711, Dec. 2005, doi: 10.1016/j.ndteint.2005.04.002.

[17] D. Gabor, “Theory of Communication,” Journal of the Institution of Electrical Engineers, vol. 96, pp. 429-441, 1946.