著者:Nicolas Badeau、Guillaume Painchaud-April、Chi-Hang Kwan
要約
トータルフォーカシングメソッド(TFM)検査法は、非破壊検査(NDT)を規定する基準や規格(ASME Section Vなど)に盛り込まれるようになっています。TFMスキャンプランに関するこれらの基準に明記されている重要なパラメーターの1つに、振幅忠実度があります。これは、イメージンググリッドの有限分解能のために、指定された反射源に対して取得される振幅の変動として定義されます。基準の標準的な許容振幅忠実度しきい値は、最大2 dBです。特定の設定の振幅忠実度を測定するための実験方法は、基準で提示されていますが、本稿ではシンプルで保守的な分析方法を提案します。振幅忠実度の推定ではTFMエンベロープの使用も考慮されますが、これは振幅忠実度の値が確立許容誤差を超えることなく、低密度なTFMグリッドを使用できるためです。実験結果から、標準TFMイメージングの場合、2 dB未満の振幅忠実度を得るには約λ0/10のグリッド分解能が必要なことが分かりました。同じく実験結果から、エンベロープを使用するTFMイメージングでは、基準に準拠するにはグリッド分解能λ0/3.3が必要であることが示されました。
はじめに
トータルフォーカシングメソッド(TFM)は、コンポーネントの非破壊検査(NDT)法として新たに受け入れられています。ASME V [1]などの基準や規格は、フルマトリックスキャプチャ(FMC)やTFMを追加の超音波フェーズドアレイ検査方法として統合しています。FMC/TFMはNDT業界では比較的新しい技法ですが、医療分野ではかなり前から医用超音波イメージングの代表的技法として使用されています[2–4]。実際、ほとんどの医用超音波イメージング法が基準とされTFMイメージングと比較されています。
いくつかの技法はFMC/TFMと似ていますが(VTFM [5]、IWEX [6]、SAFT [7])、使用されている大半の共通アルゴリズムは遅延和処理です [2–4,8,9]。FMC/TFM技法は、データ収集スキーム(FMC)と合成スキーム(TFM)から構成されます。FMCではすべての送受信素子の組み合わせからの信号収集を基にします。TFMでは対象領域内の複数の位置で超音波ビームを集束させた結果を計算します。TFMの対象領域はデカルト座標系に重ねられることが多く、音響集束が適用される個々のグリッド交点はピクセルと呼ばれます。この集束方法は標準的な超音波フェーズドアレイイメージングと似ていますが、後処理のビーム形成にデータのFMCマトリックスに保存されたデータが使用される点が異なります。データ収集後の遅延和処理では、標準的なNDTアプリケーションで見られる基本的な音波の直線性を前提とします。
FMC/TFM技法は、従来のフェーズドアレイ法の自然な発展形と見ることができます。ただし、従来の超音波フェーズドアレイ検査(PAUT)とはデータ表現が異なるため、新たな設定パラメーターを考慮する必要があります。このような概念の1つが、TFMグリッドの振幅忠実度(AF)です。AFは、TFMグリッド解像度{Δx,Δz}が原因で生じる、表示の最大振幅変動と定義されます。一様なデカルト座標系の使用((Δx=Δz)など)については後述します。振幅忠実度は正式に以下のように表すことができます。
![(式1) AF(Δx)≡-20 log (A_(sampled max) (Δx))/A_(true max) [dB]](https://industrial.evidentscientific.com.cn/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_01.jpg?rev=43A1)
ここで、Asampled maxは有限グリッドサンプリングに基づいて測定された対象形状の最大振幅、Atrue maxは無限グリッド解像度に基づく同じ対象形状の最大値です。Asampled max (Δx)の2本の軸に対してグリッドサイズが0になる限界はAtrue maxを表し、対応する振幅忠実度は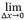 AF(Δx)=0になります。式1は、グリッド解像度に対して振幅忠実度を求める公式な定義です。ただし実際は、基本となる信号の真の最大値Atrue maxを推定するには、TFM振幅画像のオーバーサンプリングと補間が必要です。
AF(Δx)=0になります。式1は、グリッド解像度に対して振幅忠実度を求める公式な定義です。ただし実際は、基本となる信号の真の最大値Atrue maxを推定するには、TFM振幅画像のオーバーサンプリングと補間が必要です。
![(式2)(AF) ̂(Δx)=-20 log (A_(sampled max) (Δx))/A ̂_(true max) [dB]](https://industrial.evidentscientific.com.cn/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_02.jpg?rev=43A1)
ここで、 true maxはAtrue maxの推定量です。
true maxはAtrue maxの推定量です。
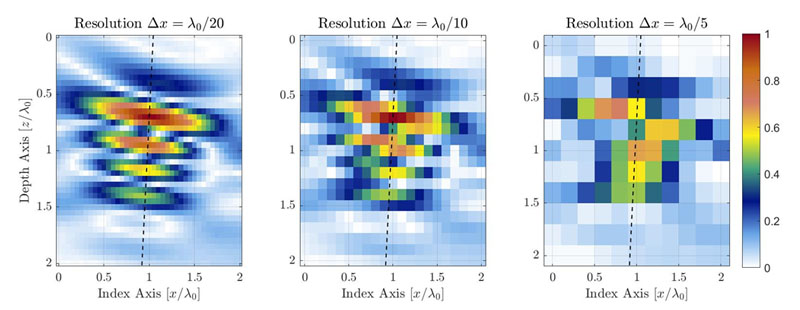
図1:TFMグリッド解像度を低くしたことによるTFM画質の低下を示す図。破線は音響伝搬の主軸を表します。
対象の同一領域について、グリッド解像度が粗いとピクセル数が低くなります。図1に、グリッド解像度値が異なる同じ横穴(SDH)の標準的なTFM画像を示します。グリッド解像度はプローブの中心周波数波長の分数λ0= c/f0として定義されます。ここで、cは試験体の音響速度、f0はプローブの中心周波数です。
規格と基準には、振幅忠実度の要件を最大2 dBと記載されるようになりました [1,10]。この要件が生じたのは、適切なNDT分析を確実に行うための十分な画質と、所定の対象領域にわたるTFMグリッドの密度によって大きく影響を受ける検査効率の、実用的な妥協策によるものです。TFMの画質と検査効率のバランスは、大きな処理能力へのアクセスを持たない自律型ポータブル装置にとっては特に重要です。内蔵ハードウェアの電力効率が改良され、遠隔計算処理が広く利用可能になるにつれて、この問題は解消されると思われます。
いくつかの経験的方法が提案されてきましたが[10–12]、大規模な計算を必要とするものが多く、得られた結果はグリッド解像度が原因で真の振幅を表していません。この問題については後のセクションで説明します。本稿では、NDT技術者が基準に準拠した効率的なTFM検査を実施できるように、TFM設定の振幅忠実度を正確に推定するための方法について示します。
本稿は以下のように分かれています。はじめに、NDT技術者が直面する問題の包括的な説明を行います。次に、TFM設定の振幅忠実度を経験的に測定する方法について説明します。振幅忠実度を推定するための分析モデルを次のセクションで提案します。そして3つの異なるTFM使用例について、提案モデルと経験的測定を比較します。最後に簡潔な結論を示して論文を締めくくります。
課題
非常に細かい(高密度)グリッドは非常に小さな振幅忠実度を可能にしますが、ライブTFM画像の計算処理能力のある現代の電子機器でも計算限界があります。特定の対象領域にわたる細かいグリッド解像度は、計算すべき集束点が大量にあることを意味し、検査効率と機械的スキャン速度が低下します。NDT技術者は、基準の準拠を維持しつつ検査効率を最大化する適切なグリッド解像度を選択できなければなりません。
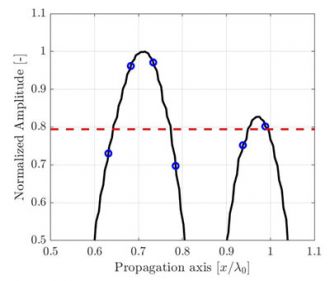
振幅忠実度は、さまざまな周期の単純な1次元信号サンプルで示すことができます。図2の例は、図1に示したSDHの振幅を音響伝搬軸に沿って示したもので、高解像度λ0/100画像から取得されています。例として取り上げるため、信号最大振幅に近い部分のみを拡大して示しています。また、3つの異なる解像度λ0/20、λ0/10、λ0/5での測定値が、高解像度の補間基準(黒い曲線)の上に青い円で示されています。
(a)離散グリッド解像度はλ0/20、計算された振幅忠実度はAF = 0.27 dB。 |
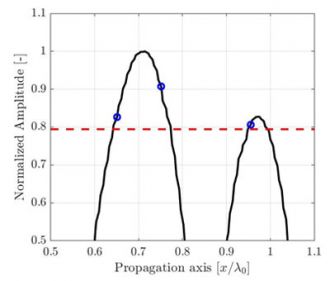
(b)離散グリッド解像度はλ0/10、計算された振幅忠実度はAF = 0.82 dB。 |
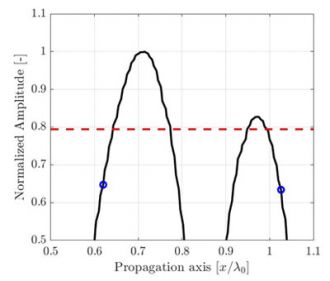
(c)離散グリッド解像度はλ0/5、計算された振幅忠実度はAF = 3.7 dB。 |
図2:図1に描かれた伝搬軸に沿って記録された振幅へのサンプリング周期作用を表す図。高解像度の補間信号基準(黒い線)が視覚補助のために示されています。基準に準拠する振幅忠実度2 dBは赤い破線で示されています。
明白な結論として、式1で数値化したAF値のとおり、グリッド密度が高いほど連続信号が良好に表されますが、最適化の問題は残ります。TFM画像上の考えられるすべてのグリッド位置について、目標値AFtargetに等しい振幅忠実度 を保証する最大グリッドサイズ(Δxmax)は何か、という問題です。つまり、次のようになります。
を保証する最大グリッドサイズ(Δxmax)は何か、という問題です。つまり、次のようになります。
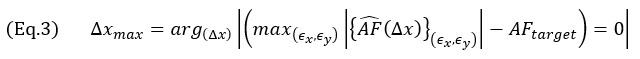
この問題文から明らかなように、固定セルサイズ(Δx)の最大 を取得するには、変位量(ϵx,ϵy)で示されるすべてのグリッドの平行移動を考慮する必要があります。これは、TFM画像を計算するために考えられるすべてのグリッド位置をカバーすることを目的としています。
を取得するには、変位量(ϵx,ϵy)で示されるすべてのグリッドの平行移動を考慮する必要があります。これは、TFM画像を計算するために考えられるすべてのグリッド位置をカバーすることを目的としています。
次のセクションでは、複数のグリッド変位量{ (Δx)}(ϵx,ϵy)から求めた、振幅忠実度値の測定原理図を示します。
(Δx)}(ϵx,ϵy)から求めた、振幅忠実度値の測定原理図を示します。
振幅忠実度の経験的測定
シンプルな分析モデルを使用した振幅忠実度の推定方法を示す前に、TFM画像について経験的に測定する方法を定義することが非常に重要です。NDT業界では複数の技法が説明、提案されていますが[10–12]、振幅忠実度について完全に定量化していないものもあります。振幅忠実度の経験的測定では、複数の正確なTFMグリッド位置から大量のTFM画像を計算する必要があるため、すぐにNDT技術者の負担になる可能性があります。
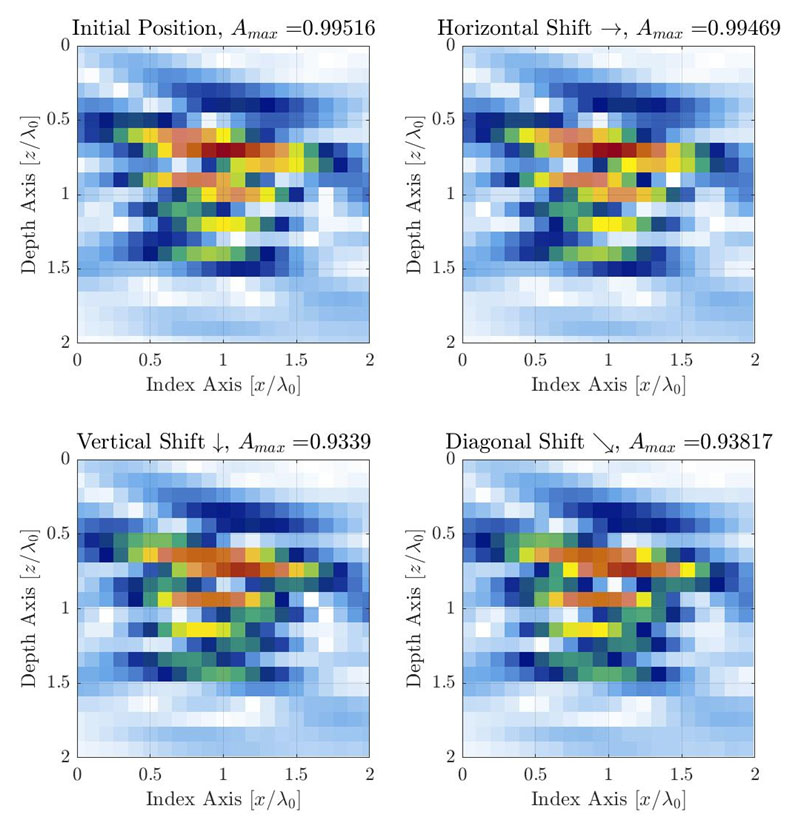
図3:グリッドを3方向に移動した場合の、離散グリッド解像度により生じるAF変動を表した図。グリッド解像度はΔx=Δy=λ0/10に設定されています。グリッドはグリッドセルの4分の1ずつずれます。右方向(ϵx=λ0/40,ϵy=0)(右上)、下方向(ϵx=0,ϵy=λ0/40)(左下)、斜め方向(ϵx=λ0/40,ϵy=λ0/40)(右下)。
標準的なTFMアプリケーションの場合、SDHは振幅校正と振幅忠実度の測定用の基準欠陥として使用します[1,10]。観察される振幅は、音響伝搬の主軸に沿って最も変動する、対象領域内のプローブ、ウェッジ、ターゲット位置の関数です(プローブに対するTFMグリッド位置など)。図1に示した例で、伝搬の主軸はほぼ垂直です。ただし一般的な測定法では、伝搬軸は対象領域内の位置によって異なります。TFM画像の場合、離散グリッドによる真の振幅の変動を取得するには、サンプリンググリッドをあらゆる方向に移動する必要があります。この処理を、図1(中央)のグリッド解像度λ0/10と同じ例を使って以下に示します。
グリッドは、検査対象グリッド解像度を少しずつ(例えば、解像度の約12分の1ずつ)、グリッドのオーバーラップが必要なだけあらゆる方向に移動することが推奨されます。つまり、2つの直交方向のうち1つのグリッド解像度のオフセットをカバーするには、合計202 = 400移動ステップが必要です(解像度の12分の1の推奨グリッドステップを使用する場合)。最大振幅はグリッドオフセットごとに記録され、そのうち最大値と最小値は式2による振幅忠実度の取得に使用されます。図3の例で、グリッド解像度はλ0/10、測定された振幅忠実度は0.88 dBです。必要な移動の数で判断すると、この手動プロセスはNDT技術者にとって面倒で時間がかかります。単一のグリッド解像度の振幅忠実度を測定するために、合計400ものTFM画像を計算する必要があることも意味します。
特筆すべきは、ASME Section V [12]で提案されているように試験体に対してプローブを機械的に移動する代わりに、プローブに対するTFMグリッド位置のソフトウェア移動を使用すれば、単一のFMCデータセットから複数のTFM画像を生成できることです。この方法のもう一つの利点は、グリッドの垂直方向の部分にアクセスできる点です。実際、選択したSDHに対して深さ軸に沿って、プローブとウェッジを機械的に動かすことはできません。
一部のNDT機器はセミオートマチックツールとして、TFMグリッドをずらして対象領域内の最大振幅を記録し、最終的に振幅忠実度を計算します[11]。ただし、こうしたツールがグリッドをずらすのは水平方向のみで、振幅忠実度が小さく推定されます。比較のため、例えばグリッドを水平軸に沿って単独に移動した場合(図3)、測定される振幅忠実度は0.06 dBで、垂直軸を考慮して測定した振幅忠実度より15倍以上低くなります。
振幅忠実度推定の現象論モデル
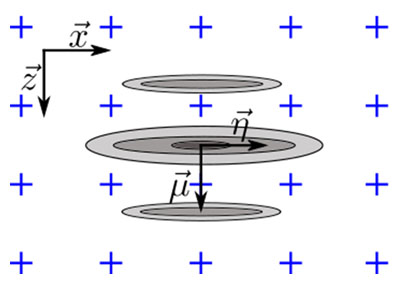
このセクションでは、経験的観察に基づくシンプルな分析モデルを提案します。現象論モデルでは、伝搬の主軸に沿った信号動作を考慮し、そこに振幅の変動が最も現れると仮定するため、グリッド解像度に対して非常に感度が高くなります。図4に、伝搬の主軸に沿ったSDH(青)とビームウエスト軸に沿ったSDH(赤)のTFM画像の経験的形状を示します。軸の起点は明らかにエンベロープ表示の最大振幅の位置にあり、振動表示の軸 に沿って少しオフセットがあることを示しています。標準振動TFMとTFMのエンベロープのプロファイルを示します。
に沿って少しオフセットがあることを示しています。標準振動TFMとTFMのエンベロープのプロファイルを示します。
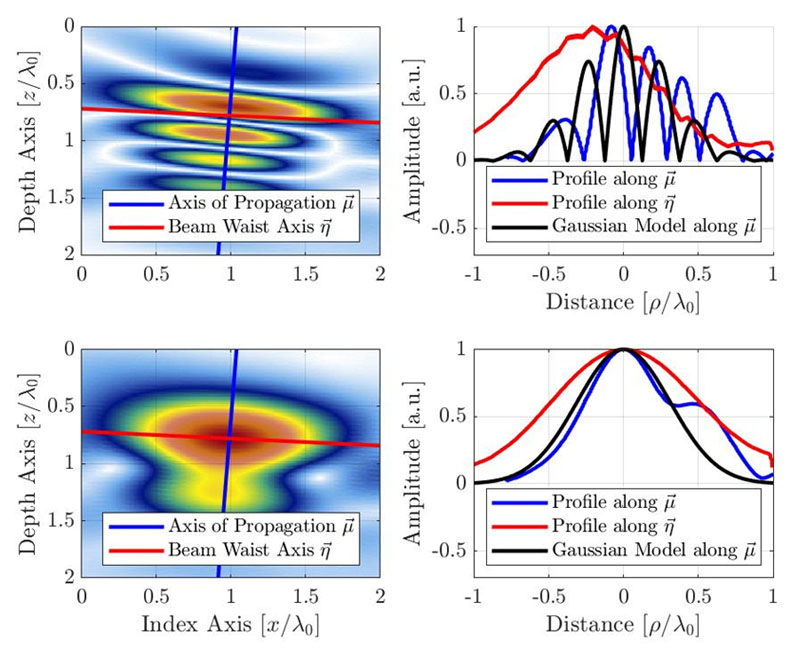
図4:TFM画像(上:振動、下:エンベロープ)と、音響伝搬軸とビームウエスト軸に沿った信号プロファイル。提案されるガウスモデルも、振動画像とエンベロープ画像のそれぞれに描かれています。TFMビーム形成が持つパルスエコーの性質から、明白な波長は半分になっています。
前述のように、最大振幅変動の軸は音響伝搬の主軸に沿っていると想定されます。したがって、モデルはこの方向に振幅の変動を再生成することを目指しています。モデル信号はコサイン変調ガウスです。
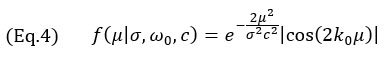
ここで、k0=ω0/cはプローブの中心角周波数ω0の波数、σは中心周波数と相対帯域幅bwに依存する幅パラメーターです。幅パラメーターσは以下を使用して計算されます。
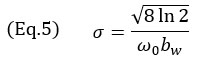
標準的なNDTフェーズドアレイプローブの場合、相対帯域幅は60%付近であるため、値(bw=0.6)がモデルに使用されます。これによって、ガウスエンベロープが単一コサイン振動より大きくなります。特筆すべきは、式3のコサイン項の中心周波数が、プローブの中心周波数の倍である点です。これはTFMイメージングが持つパルスエコーの性質(送受信路程)によるもので、図4の振動間の距離に見られます。実際、時間領域と空間領域の変換は、μ = tc/2と表されます。これは、式3の指数項に係数2が用いられていることの説明にもなります。
式4の振動モデルの場合、ガウスエンベロープがコサイン関数の単一振動よりはるかに大きく、大きい値ほどAFの空間エイリアシングが発生するため、値|μ|≤λ0/8のみが考慮されます。
TFMエンベロープモデルの場合、式4のガウス項のみを使用して以下のようになります。
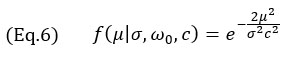
これはあらゆるグリッド解像度に有効です。式3と7のモデルから得られたプロファイルを、図4の実験プロファイルに並んで示しています。経験的測定では、メインエコーに遅れて表面波(SDHの典型的な「巻き込み」エコー)も表示されますが、提案モデルには明らかに存在しません。
このモデルの振幅忠実度について最悪のシナリオを得るには、グリッド直交軸に対する欠陥の方向を考慮する必要があります。図5aに示すように、振動TFMの最悪のシナリオが発生するのは、音響伝搬の主軸 がグリッド軸のいずれかと平行になる場合です。したがって振幅忠実度の計算は、最大振幅が軸
がグリッド軸のいずれかと平行になる場合です。したがって振幅忠実度の計算は、最大振幅が軸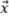 または
または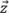 に沿った2つのグリッド点の中心であるかのように計算する必要があります。以下のようになります。
に沿った2つのグリッド点の中心であるかのように計算する必要があります。以下のようになります。
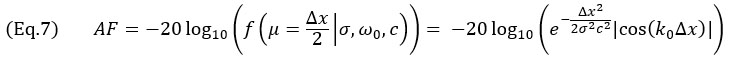
このとき、Δx≤λ0/4です。TFMエンベロープの場合、最悪のシナリオが発生するのは、振幅プロファイルが音響伝搬の主軸 とビームウエスト軸
とビームウエスト軸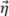 に沿って同一である場合です。この例(図5b)はSDHが円を表す場合に対応するため、伝搬の主軸
に沿って同一である場合です。この例(図5b)はSDHが円を表す場合に対応するため、伝搬の主軸 はあらゆる方向を取り得ます。最悪のシナリオが発生するのは、図のようにSDHエコーが4つの隣接点の中心にある場合です。この場合、振幅忠実度はグリッドの対角線に沿って計算する必要があり、実質的に以下のようになります。
はあらゆる方向を取り得ます。最悪のシナリオが発生するのは、図のようにSDHエコーが4つの隣接点の中心にある場合です。この場合、振幅忠実度はグリッドの対角線に沿って計算する必要があり、実質的に以下のようになります。
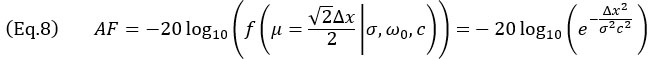
NDTアプリケーションで標準的な、AF値が小さい場合のAFに対する値Δxの近似形は、式7の振動モデルの場合は以下で取得できます。

式8のエンベロープモデルの場合は以下で取得できます。
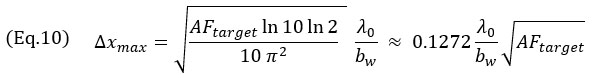
これらの式は、すべての例でAF値に対するグリッドサイズの平方根の従属関係を変換します。式9は、式7のテイラー級数2次近似を用いて取得したものです。この近似を、図6の正確なモデルに並んで示しています。また、振動モデルのグリッドサイズは、小さなbwの相対帯域幅の影響はほとんど受けません。さらに注目すべきは、振動モデルとエンベロープモデルのどちらの場合も、最大グリッド解像度Δxmaxが対象の振幅忠実度の平方根に関連する点です。現象論モデルの場合、基準に準拠するため、これらの値は最大グリッド解像度を表します。
(a)軸 |
(b)振幅プロファイルが |
図5: (a)振動TFMと(b)TFMエンベロープにおける最悪のシナリオで、グリッド直交軸に対する欠陥の方向を表す図。
実験的検証
3つの異なるTFM検査使用例に対する経験的結果を使用して、提案モデルを検証します。3つのTFM設定すべてについて、各種グリッド解像度でいくつかのSDHをイメージングし、前述した方法で振幅忠実度を測定しました。3つの使用例のパラメーターを表1に示します。最初の例は高周波数プローブ(7.5 MHz)を使用し、2つ目の例は低周波数(5 MHz)で横波を使用し、3つ目の例は高いプローブ周波数(10 MHz)と素子数で横波を使用します。すべての例で、SDHは炭素鋼試験片の上面から50 mm以内にあります。
表1:振幅忠実度の実験的検証に使用したTFM設定のパラメーター
| ケース | プローブのパラメーター | ウェッジのパラメーター | 試験体のパラメーター | TFMモード | |||||
|---|---|---|---|---|---|---|---|---|---|
|
周波数
[MHz] |
素子数
[#] |
ピッチ
[mm] |
音速
[m/s] |
角度
[°] |
高さ
[mm] |
音速
cp - cs [m/s] |
横穴
直径 [mm] | ||
| 1 | 7.5 | 64 | 1.0 | なし | なし | 0 | 3240 - 5890 | 1 | L-L |
| 2 | 5 | 32 | 1.0 | 2330 | 36.1 | 11.0 | 3240 - 5890 | 0.5 | T-T |
| 3 | 10 | 64 | 0.5 | 2330 | 36.1 | 11.0 | 3240 - 5890 | 1 | T-T |
図5に、標準的な振動TFM(上)とTFMエンベロープ(下)の振幅忠実度の結果を示します。個々の灰色の点は、使用例、SDH、グリッド解像度のさまざまな組み合わせを表します。前述のガウスモデルにより推定した振幅忠実度は、黒い曲線で示しています。赤い破線は、基準に準拠した2 dBの限度を表します。
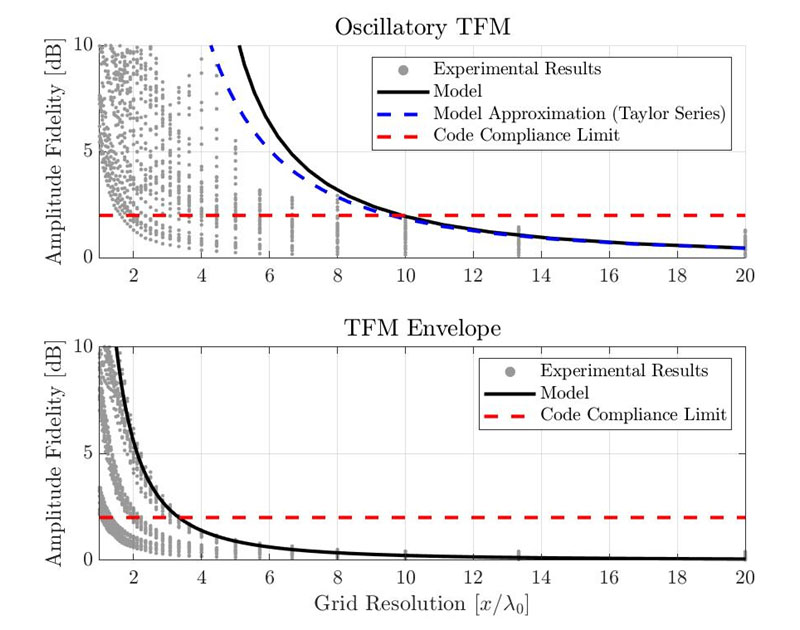
図6:標準的な振動TFM(上)とTFMエンベロープ(下)について、振幅忠実度の経験的測定と提案されるガウスモデル測定結果の比較).
提案モデルを使用すると、基準に準拠するために必要な解像度は、振動TFMの場合はλ0/9.9、TFMエンベロープの場合はλ0/3.3です。実験結果から、基準に準拠するための最小グリッド解像度は、標準的な振動TFMの場合は約λ0/10、TFMエンベロープの場合はλ0/3.3と示されます。ただし、これらの値は提示した最悪の実験例から取得したものです。測定した振幅忠実度値の中には、粗いグリッド解像度を使用した場合でも、2 dBを下回るものがあります。したがって提案モデルでは、TFM設定の振幅忠実度について良好かつ保守的な推定値が得られます。
結論
TFM設定の振幅忠実度は、グリッド解像度に関してイメージングの頑健性を左右する重要な測定値です。グリッドの密度が高いほど、振幅忠実度値は低くなります。トータルフォーカシングメソッドが新しい検査方法として基準や規格に含まれるようになり、2 dB以下の振幅忠実度が求められています。本稿では、振幅忠実度を正しく経験的に測定する方法について説明し、TFM設定の振幅忠実度を推定するためのシンプルな分析モデルを提案しました。
シンプルな分析モデルの提案は、音響伝搬の主軸に沿った振幅プロファイルに基づいています。このモデルでは、振幅プロファイルをガウス変調コサイン振動として推定します。このプロファイルを使用して、標準的な振動TFMとTFMエンベロープの両方について、優れた結果が得られる振幅忠実度を推定します。経験的結果により、標準的な振動TFMとTFMエンベロープに必要な最大グリッド解像度は、それぞれλ0/10、λ0/3.3と示されました。提案分析モデルで推定される必要なグリッド解像度は、標準的な振動TFMの場合はλ0/9.9、TFMエンベロープの場合はλ0/3.3です。したがって提案モデルは、TFM設定の振幅忠実度の推定に使用することができます。
基準準拠ソリューションとしてTFMエンベロープを使用する利点については、ホワイトペーパー「エンベロープ機能を利用したトータルフォーカシングメソッドの使用」をご覧ください。
参考文献
[1] ASME Committee, 2019, “ASME BPVC.V Article 4 Mandatory Appendix XI Full Matric Capture.”
[2] Oralkan, O., Ergun, A. S., Johnson, J. A., Karaman, M., Demirci, U., Kaviani, K., Lee, T. H., and Khuri-Yakub, B. T., 2002, “Capacitive Micromachined Ultrasonic Transducers: Next-Generation Arrays for Acoustic Imaging?,” IEEE Trans. Ultrason., Ferroelect., Freq. Contr., 49(11), pp. 1596–1610.
[3] Thomenius, K. E., 1996, “Evolution of Ultrasound Beamformers,” 1996 IEEE Ultrasonics Symposium. Proceedings, IEEE, San Antonio, TX, USA, pp. 1615–1622.
[4] Freeman, S., Li, P., and O’Donnell, M., “Retrospective Dynamic Transmit Focusing,” p. 24.
[5] Wilcox, P. D., 2006, “Exploiting the Full Data Set from Ultrasonic Arrays by Post-Processing,” AIP Conference Proceedings, AIP, Brunswick, Maine (USA), pp. 845–852.
[6] Portzgen, N., Gisolf, D., and Blacquiere, G., 2007, “Inverse Wave Field Extrapolation: A Different NDI Approach to Imaging Defects,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 54(1), pp. 118–127.
[7] Sharpe, R. S., ed., 1982, Research Techniques in Nondestructive Testing. Vol. 6: ..., Acad. Press, London.
[8] Holmes, C., Drinkwater, B. W., and Wilcox, P. D., 2008, “Advanced Post-Processing for Scanned Ultrasonic Arrays: Application to Defect Detection and Classification in Non-Destructive Evaluation,” Ultrasonics, 48(6–7), pp. 636–642.
[9] Holmes, C., Drinkwater, B. W., and Wilcox, P. D., 2005, “Post-Processing of the Full Matrix of Ultrasonic Transmit–Receive Array Data for Non-Destructive Evaluation,” NDT & E International, 38(8), pp. 701–711.
[10] ISO, 2020, “ISO/DIS 23865 -FMC-TFM - General Use of TFM-FMC Technique.”
[11] Johnson, P., 2019, “With a New Software Wizard, There’s No Sorcery but the Magic of the M2M Gekko Is Evident with Instant Code Compliance for Your TFM Weld Inspections.,” Code Compliant TFM Weld Inspection with Three Clicks.
[12] ASME Committee, 2019, “ASME BPVC.V Article 4 Nonmandatory Appendix F - Examination of Welds Using Full Matrix Capture.”