1. はじめに
超音波非破壊検査(NDT)の分野において、現在、トータルフォーカシングメソッド(TFM)はNDTイメージング法として広く知られ、受け入れられています。さらに、この手法はOmniScan™ X3シリーズ探傷器など、いくつかのポータブル機器に搭載されたものが入手可能なので、TFMはNDT業界内で人気が高まっています。
しかし、TFMは従来のフェーズドアレイ(PA)検査よりは画像解釈が容易ですが、データ取得時の発信に単一素子を使用するため、画像のSN比(SNR)が低くなります。この低いSNRの原因は、厚い試験体や減衰量の多い材料などで見られる、貧弱な音響浸透によるものです。
この問題に対処するため、従来のTFMアルゴリズムとは異なり、取得信号のうち位相に関する情報のみを使用する手法を本稿で提案します。これはベクトルコヒーレンス因子(VCF)1に基づきます。VCFは、取得した信号から振幅情報を除去する画像そのものとして使用されます。この手法は一般に位相コヒーレンスイメージング(PCI)としても知られ、以下を含むいくつかの利点2,3,4があります。
- PCIでは信号の瞬時位相のみが考慮され2、材料減衰は信号の位相に影響しないため、厚みのある材料や減衰量の多い材料を検査する場合の問題解決に特に役立つ。
- 信号の振幅は考慮されないので、振幅を校正する必要がない。3
- 回折形状に対する感度の向上と、さまざまなスキャンビューにおける欠陥表示の一貫性。
- 亀裂状欠陥のサイジングに適した、非振幅ベースの確実な手法である。3
本稿の残りの部分では、EvidentのPCI技術の基本原理について説明します。その一部、特に音響エコー信号の2値化表現の生成方法は特許出願中です。この説明のため、まず遅延加算(DAS)アルゴリズムの演算について確認します。このアルゴリズムは、FMCからのエンベロープを使用して、従来のTFM画像を構築できるようにするものです。次に、PCIアルゴリズムがDASアルゴリズムの変形を成していることについて説明します。
既知の性質と形状を持つ人工的な欠陥を使用して実際の使用例を見ることで、2種類のアルゴリズムにより取得された従来のTFMとPCI5という2種類の画像を比較できます。
2. 従来のTFMとDASアルゴリズムの原理の確認

図1:試験体表面に接触したプローブによるFMCデータ収集の幾何構造。圧電素子kが材料に向かって超音波を発信します。圧電素子lが反射した超音波を受信します。
図1は、フェーズドアレイ超音波探傷プローブ(PAUT)からのフルマトリックスキャプチャ(FMC)データ収集の幾何構造と、FMCを使用して検査および表示する試験体部分に対応する関心領域(ROI)を示しています。圧電素子kが超音波を発信します。この音波は試験体の材料内を伝搬し、さまざまな界面のほか、材料内に存在する欠陥によって反射されます。圧電素子lは反射した超音波を受信し、A-スキャン信号sklを形成します。次にFMCによって、考えられるすべてのklの組み合わせのA-スキャンがすべてまとめられます。
図2は、FMCデータ収集から従来のTFM画像を再構築する、遅延加算(DAS)アルゴリズムの原理の主な6つのステップを表すフローチャートです。
- FMCデータ収集が実行され、すべてのA-スキャンsklI (t)で構成されるデータが生成されます。指数Iは、これらのA-スキャンが同相信号であることを示します。
- ヒルベルト変換を適用すると、収集されてFMCデータにまとめられた同相A-スキャンsklI (t)の直交成分sklQ (t)を取得できます。
- 事前計算された遅延τkl (x,z)を使用して、xklIデータとxklQデータが抽出されます。この遅延の事前計算は、選択したモードの種類(L-L、T-T、TT-T、TT-TTなど)と観察対象ROIに従って行われます。
- 次に総和により、直交の2つのTFM画像、ITFMI (x,z)とITFMQ (x,z)が得られます。
- 振幅(加群やエンベロープともいう)ITFM (x,z)が、ユークリッド距離計算を使用して推定されます。
- グラフィックスカードにより有効になる事後処理ステップで、TFM画像が形成され(基本的にはデジタルフィルタリング、再サンプリング、再サイジング)、ユーザーの装置ディスプレイに表示されます。
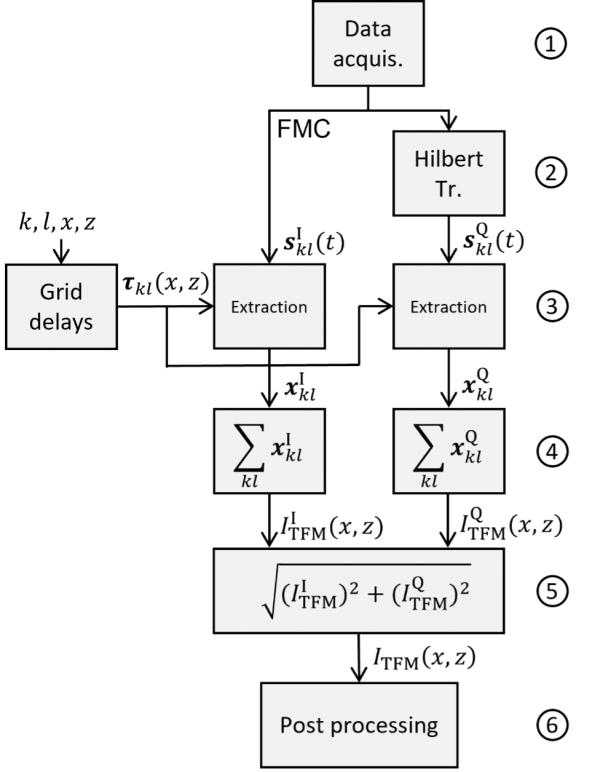
図2:FMCデータ収集から振幅TFM画像を取得するためのDASアルゴリズムの原理(6ステップ)
3. PCIアルゴリズムの原理
OmniScan X3 64探傷器に導入されたPCIアルゴリズムが、従来のTFMやその他の位相ベースの信号処理技術と主に異なるのは、革新的な音響信号の2値化コンポーネント(特許出願中)が含まれていることです。PCIアルゴリズムを図2のDASアルゴリズムと比較すると、主に2つの点が異なります。
- 符号関数を使用した、信号sklI (t)とsklQ (t)の数値化からなる追加ステップ3b(図4)。このステップによって、後述するように信号コヒーレンスの強調が可能になります。
- 振幅の計算に、従来のTFMで使用したユークリッドノルムではなく、L∞ノルム(チェビシェフノルムともいう)を使用する。
3.1. 位相コヒーレンスの概念
PCIの性質を深く理解するには、この手法の基本原理である信号コヒーレンスの概念を知る必要があります。この項で簡単に概念について説明します。このためには、符号関数の演算に注意を払う必要があります。
符号関数は3つの異なるレベル+1、0、-1で信号s(t)を数値化します。

信号に対するこの数値化演算の作用をよりよく理解するため、例証の目的で任意に選択したA-スキャンs(t)に対する符号関数の適用結果を図3に示します。図3を観察すると、以下のことがわかります。
- 信号には2種類のゾーンがあります。(1)いわゆるコヒーレントゾーン:欠陥指示の存在を示し、欠陥の存在を表します。(2)いわゆるノンコヒーレントゾーン:欠陥指示がなく、純粋なノイズの存在を示します。このノイズは主に装置固有の電気ノイズですが、音波と試験体の材料との相互作用に関連する構造上のノイズもあります。
- 量子化信号のコヒーレントゾーンでは信号の強度は一定で、1から−1の間に含まれ(図3(b))、生信号の場合は時間とともに振幅が小さくなっています(図3(a))(形状的な減衰などによる)。
- 図3:(b)の量子化信号では、強いノイズが無秩序な様相で存在し、図3(a)の生信号ではほとんど感知できないノイズレベルと比べて、ずっと高いレベルにあります。この状態および後で示す例から、PCIで取得されたTFM画像が従来のTFM画像より「ノイズが多く」見える理由がわかります。これは図6(a)と図6(b)、または図8(a)と図8(b)で比較できます。ただし、無秩序なノイズが高いレベルで存在する(ノンコヒーレント)領域には、コヒーレント領域とは異なり、画像内の位置とは無関係に統計的分布が見られます。この違いから、ノイズが多く見えても、PCIで生成された画像ではコヒーレント領域をノンコヒーレント領域と簡単に区別できます。OmniScan X3 64探傷器でPCIの使用時にデフォルトで適用される適合カラーマップでは、ユーザーは簡単にこれを見分けられます(図6(c)と図8(c)を参照)。
したがって符号関数の作用をPCIに用いる理由5は、一方では信号強度を(検査の深さなどに関係なく)一定に保つためで、他方では欠陥の存在に対応しやすいコヒーレントゾーンを、欠陥のない無秩序なノンコヒーレントゾーンから区別するためです。留意すべきは、信号のコヒーレンス情報は信号の位相によって運ばれるということです。
ある視点から見ると、PCIによって伝達される情報は、実際には「コヒーレンス/ノンコヒーレンス」と「欠陥あり/欠陥なし」が等しい、疑似バイナリと見なすことができます。次の問題は、これらの2つの型を区別する戦略の策定です。この解決方法については本稿では取り上げませんが、OmniScan X3 64探傷器に導入されているような適合カラーマップは、この分離作業に役立ちます。

図3: A-スキャンタイプの生信号とノイズ(a)と符号関数を使用する量子化信号(b)。
3.2. PCIアルゴリズム

図4:PCIアルゴリズムの原理。
図4のフローチャートは、OmniScan™ X3 64探傷器に導入されている以下のPCIアルゴリズムをまとめたものです。
- すべてのA-スキャンsklI (t)からなるFMCデータが構築されるデータ収集段階。指数Iは、これらのA-スキャンが同相信号であることを示します。
- ヒルベルト変換を適用すると、収集されてFMCデータにまとめられた同相A-スキャンsklI (t)の直交成分sklQ (t)を取得できます。
- 遅延τkl (x,z)を使用した、データxklIとxklQの抽出。この遅延の計算は、選択したモードの種類(L-L、T-T、TT-T、TT-TTなど)と観察対象ROIに従って事前に行われます。
この最初の3ステップは、図2のDASアルゴリズムのステップと同じです。
3b. 方程式1に従って符号関数を使用した、信号xklIとxklQの量子化により、信号yklIとyklQが導き出されます。

ステップ3bは、PCIアルゴリズムに固有の追加ステップです。
4. 総和により、直交の2つのPCI画像、IPCII (x,z)とIPCIQ (x,z)が得られます。
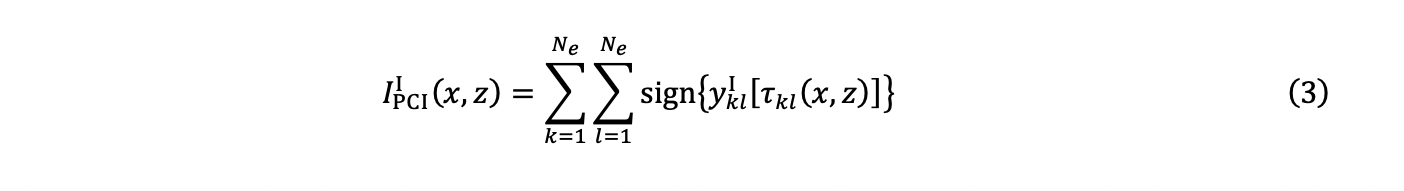
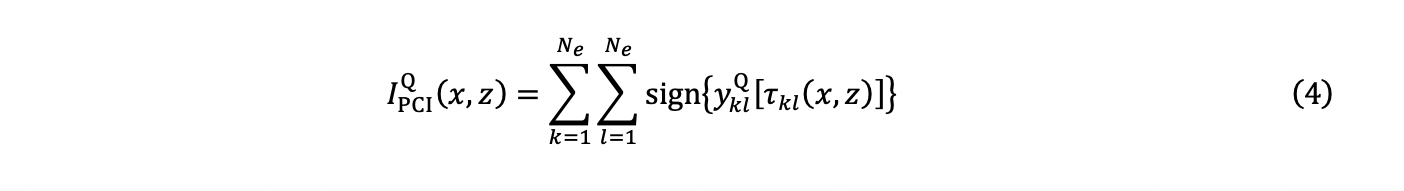
5. 次に、チェビシェフ距離(一様ノルム、L∞ノルムともいう)と、方程式(3)と(4)の2つの要素を使用して、振幅IPCI (x,z)が推定されます。
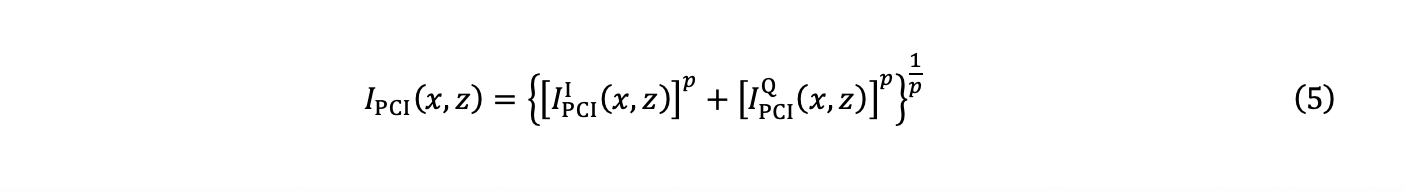
このとき、p→∞です。
方程式5から振幅を推定するのは、p→∞の場合は困難です。以下の式を使用すると、優れた近似値が得られます。
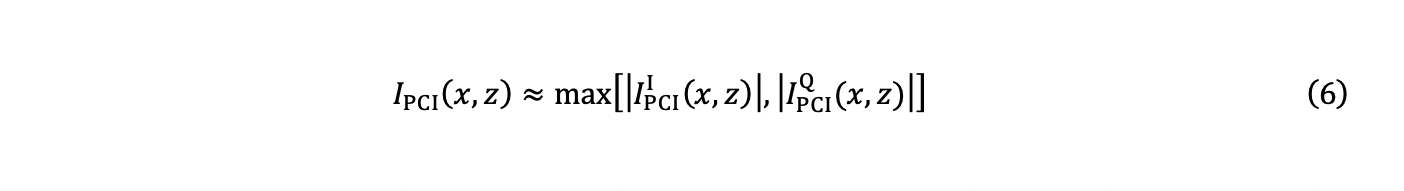
つまり、同相と直交の画像の絶対値(|⋅|)の最大値が最終値として保持されます。
6. 最後に、DASアルゴリズムの場合と同じ、グラフィックスカードにより有効になる事後処理ステップがあります。従来のTFM画像が形成され(基本的にはデジタルフィルタリング、再サンプリング、再サイジング)、ユーザーの装置画面に表示されます。
注目すべきは、図4に示した、OmniScan X3 64探傷器に導入されているPCI処理ワークフローが、従来のTFMとほとんど同じ速さで、検査中にリアルタイムで(つまりデータ収集から画像生成まで)完了する点です。
4. 実験例
以下に示す2つの例は、既知の性質と形状を持つ欠陥に対する実験的測定から抜粋したもので、前述の2つのアルゴリズムを使用して取得した画像を比較し、PCIの特定の性質を強調することを目的としています。こうした性質には、振幅の頑健性と欠陥端部の感度が含まれます。
4.1. 例1:横穴(SDH)試験片
最初の検査例は、PCI法の減衰に強い特性を強調することを意図しています。この検査では、17個のSDHを持つ鋼片(ASTM E2491低炭素鋼試験片)に対して、5L64-A32 PAUTプローブをウェッジなしで(つまり、プローブを試験体に直接接触させて)使用しました。この検査構成を図5に示します。
図6は、L-L伝搬モードを使用して再構築された従来のTFM画像(a)とPCI画像(b、c)を示しています。図6から、以下のことがはっきりと観察できます。
- PCI画像ではすべてのSDHが同じ強度で表示されているのに対して、従来のTFM画像では、下の方のSDHに減衰作用が見られ、上の方のSDHに発信されたビーム振幅の作用が見られます。
- PCI画像の例ではバックグラウンドノイズレベルも高くなっています。
PCIは振幅フリーのイメージング法なので、信号のコヒーレント合成は信号振幅とは無関係に行われ、生成される欠陥指示のコントラストレベルが高くなります。3

図5:例1の検査構成:ASTM E2491低炭素試験片と5L64-A32プローブ。
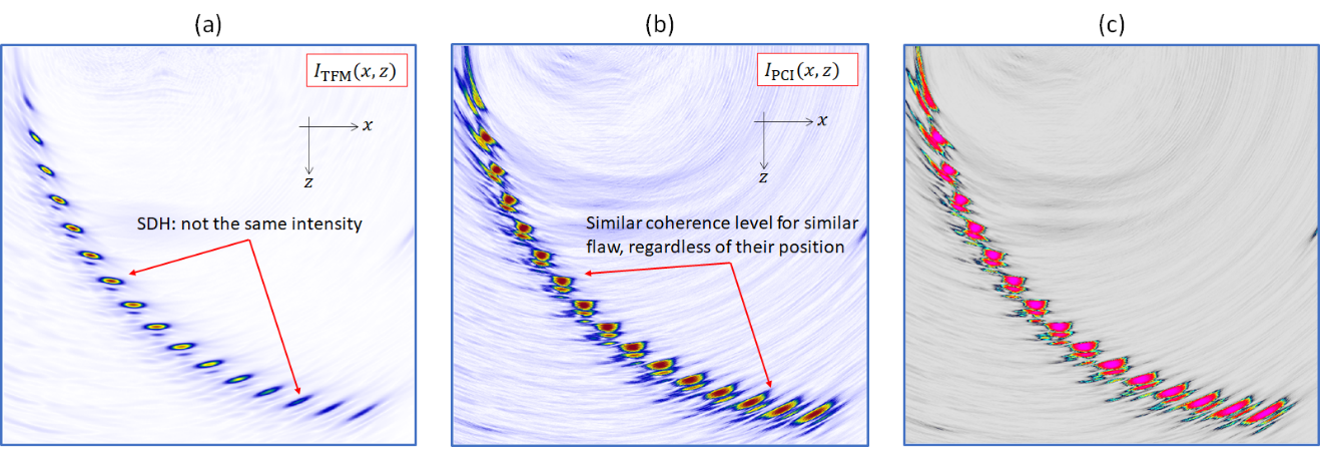
図6:SDHイメージング:従来のTFM(a)、PCI(b)、OmniScan X3 64探傷器に導入されているデフォルトのカラーマップを使用したPCI(c)
4.2. 例2:鉄鋼試験片のノッチ欠陥
PCIが持つもう一つの興味深い特性は欠陥端部に対する感度で、不連続部の正確なサイジングが可能になります。振幅合成に寄与するのはわずかな共通の位相条件なので、大きな散乱体からの鏡面反射が抑えられます。そのため、PCIは細く尖った反射源に対する頑健性が高い傾向にあります。
このPCIの特性を強調するため、2つ目の例では、表面に欠けのないノッチが70°の方向にある鋼片に対して、SPWZ1-N55S-IHCウェッジと7.5L60-PWZ1フェーズドアレイプローブを使用した検査結果を示します。この検査構成を図7に示します。
図8は、TT-TT伝搬モードを使用して再構築された従来のTFM画像(a)とPCI画像(bとc)を示しています。以下の点を比較できました。
- 振幅合成に寄与するのはわずかな共通の位相条件なので、大きな散乱体からの鏡面反射が抑えられる。
- 従来のTFMに比べてPCIはコントラストが改善されている。
- PCIは欠陥端部に対する感度が優れている。
- SN比はPCIの方が低い。
したがって、この例でノッチの範囲をより正確に評価できるのは従来のTFM画像ですが、PCIは欠陥端部に対する感度が高いのでノッチのような欠陥を正確にサイジングできます。校正処理や材料の減衰によって誤りやすい、半経験的事項を用いる必要がありません。
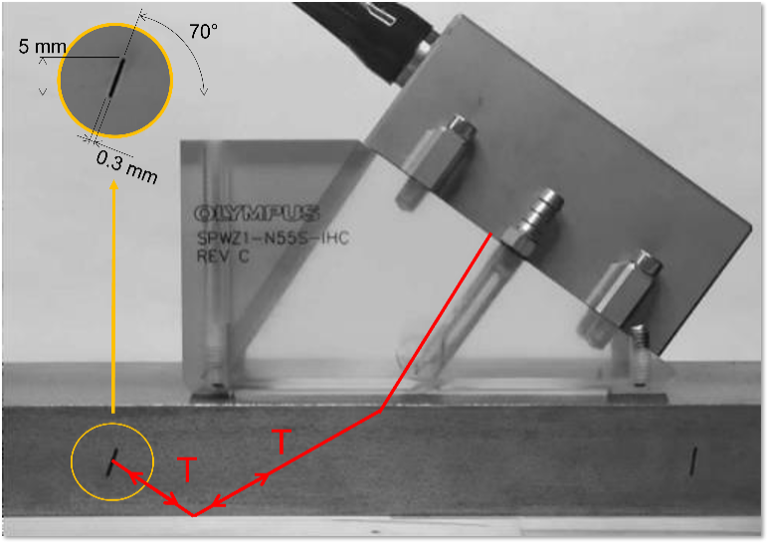
図7:例2の検査構成:傾斜のあるノッチが放電加工された低炭素鋼試験片、SPWZ1-N55S-IHCウェッジ、7.5L60-PWZ1プローブ。
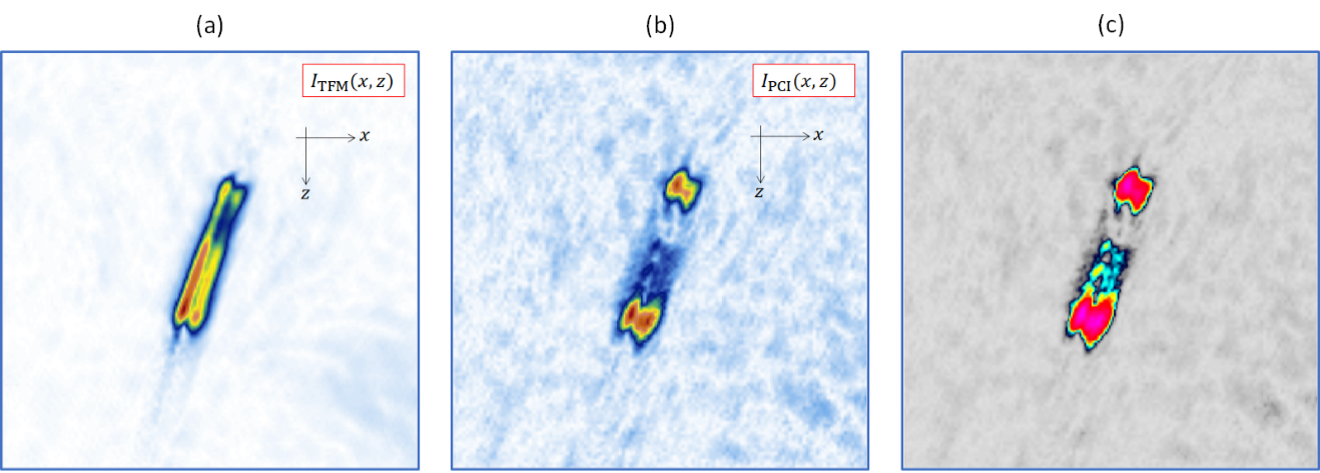
図8:ノッチイメージング:従来のTFM(a)、PCI(b)、OmniScan X3 64探傷器のデフォルトのカラーマップを使用したPCI(c)。
実験結果
結論として、実験によりPCIには多くの利点があることが示されました。
- 非振幅ベースのイメージング法であるため、画像解釈に振幅が校正された信号を使用しない点が、振幅ベースの従来のTFMより優れている。
- 細く尖った反射源や、回折を生む形状全般に対する感度が高い。
- 校正処理や材料の減衰によって誤りやすい、半経験的事項を用いる必要がなく、ノッチのような欠陥を正確にサイジングできる。
- 校正処理の必要がないため、従来のTFMよりも容易かつ正確にノッチのサイジングが可能。
- ゲインを非常に低い値に設定できるため、信号飽和が回避される。
- さらに、高性能プロセッサーを備えたOmniScan X3 64探傷器のような装置を用いれば、ライブPCI画像が生成されるので、検査中に結果がすぐに表示される。
ただし、この手法にはいくつか短所があることも言及しておきます。
- 面状反射源の再現性は弱い。
- PCIのSN比(SNR)は振幅ベースの手法より低い。ただし前述したように、PCIでは欠陥の存在を示すコヒーレント領域を、画像のノイズの多いインコヒーレント領域から区別しやすくなっている。
- ユーザーは振幅ベースの端面図を見慣れているため、調整期間が必要になる可能性がある。
参考文献
- JF Cruza, J. Camacho, and C. Fritsch, Plane-wave phase-coherence imaging for NDE, NDT & E International, vol. 87, p. 31–37, Apr. 2017.
- B. Gauthier, G. Painchaud-April, A. Le Duff, and P. Belanger, “Lightweight and Amplitude-Free Ultrasonic Imaging Using Single-Bit Digitization and Instantaneous Phase Coherence,” IEEE Trans. Ultrason., Ferroelect., Freq. Contr., vol. 69, no. 5, pp. 1763–1774, May 2022, doi: 10.1109/TUFFC.2022.3163621.
- B. Gauthier, G. Painchaud-April, A. Le Duff, and P. Bélanger, “Towards an Alternative to Time of Flight Diffraction Using Instantaneous Phase Coherence Imaging for Characterization of Crack-Like Defects,” Sensors, vol. 21, no. 3, p. 730, Jan. 2021, doi: 10.3390/s21030730.
- A. Le Duff, N. Badeau, E. Peloquin, G. Painchaud-April, C.-H. Kwan, B. Gauthier, “Total Focusing Method with Phase-Only Ultrasound Signal for Small Flaw Detection,” International Ultrasonic Testing Conference (UT-Online), 2021.
- G. Painchaud-April, A. Le Duff, C. Kwan. C. Brillon, Phase-Based Approach for Ultrasonic Inspection, World Intellectual Property Organization (WIPO). 02.09.2021. WO/2021/168565 https://patentscope.wipo.int/search/fr/detail.jsf?docId=WO2021168565=EP383773045


