作者:Nicolas Badeau,Guillaume Painchaud-April, Chi-Hang Kwan
总结
全聚焦(TFM)检测技术现已纳入无损检测(NDT)规范和标准,例如ASME规范第五节。在这些规范中,为TFM扫描计划指定的一个重要参数就是振幅保真性。振幅保真性的定义是特定反射体因成像栅格的分辨率限制而产生的振幅变化。在这些规范中,振幅保真性的典型允许阈值最大为2 dB。虽然这些规范中已经给出了测量给定设置下振幅保真性的实验方法,本文另外建议一种简单、保守的分析方法。估计振幅保真性时还可以考虑使用TFM包络,从而建立一个密度较低的TFM网格,同时不会导致振幅保真性超过规定的容差。在标准TFM成像中,经验结果表明需要约λ0/10的网格分辨率才能获得小于2 dB的振幅保真性。在TFM包络成像中,经验结果表明需要λ0/3.3的网格分辨率便能符合规范的要求。
引言
全聚焦方式(TFM)是一种最近得到公认的组件无损检测(NDT)技术。ASME V等标准和规范[1]已经集成了全矩阵捕获(FMC)和TFM,将其作为额外的阵列超声检测技术。虽然FMC/TFM技术在NDT行业中应用时间相对较短,但已作为医学超声成像的黄金标准得到应用[2-4]。事实上,大多数医学超声成像技术都以TFM成像为基准并与之进行比较。
虽然已有几种类似于FMC/TFM的技术(例如VTFM[5]、IWEX[6]、SAFT[7]),但最常用的算法是延时求和处理[2–4,8,9]。FMC/TFM技术包括采集方案(FMC)和求和方案(TFM),前者采集所有发射器和接收器元件组合的信号,而后者则计算感兴趣区域中多个位置上的聚焦超声波束的结果。感兴趣的TFM区域通常在笛卡尔网格上划分网格,而应用声聚焦的各网格交叉点则称为像素。聚焦方法类似于标准阵列超声成像,但不同之处在于波束是在对存储在FMC数据矩阵中的数据进行后处理而形成的。采集后的延时求和处理假设典型NDT应用中的主要声波具有线性。
FMC/TFM技术可看作是传统阵列技术的自然扩展。然而,其数据表示方法与传统阵列超声检测(PAUT)不同,因此必须考虑新的设置参数。其中一个概念参数是TFM网格的振幅保真性(AF)。AF的定义是由TFM网格分辨率{Δx,Δz}导致的最大振幅变化。本研究中假设使用均匀笛卡尔网格,即(Δx=Δz)。振幅保真性可正式表示为
![(公式1)AF(Δx)≡-20 log〖(A_(sampled max) (Δx))/A_(true max) 〗 [dB]](https://industrial.evidentscientific.com.cn/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_01.jpg?rev=43A1)
其中Asampled max是有限网格采样中感兴趣特征的最大测量振幅,而Atrue max是无限网格分辨率下同一感兴趣特征的最大振幅。对于Asampled max来说,网格大小在两轴上变成零时的限值(Δx)定义了Atrue max,而对应的振幅保真性变成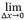 AF(Δx)=0。公式1提供了基于网格分辨率计算振幅保真性的正式定义。但在实践中,主要信号的真实最大Atrue max只能通过对TFM振幅图像过采样后插值来估计。
AF(Δx)=0。公式1提供了基于网格分辨率计算振幅保真性的正式定义。但在实践中,主要信号的真实最大Atrue max只能通过对TFM振幅图像过采样后插值来估计。
![(公式2) (AF) ̂(Δx)=-20 log〖(A_(sampled max) (Δx))/A ̂_(true max) 〗 [dB]](https://industrial.evidentscientific.com.cn/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_02.jpg?rev=43A1)
其中A ̂_ true max是Atrue max的估计值。
true max是Atrue max的估计值。
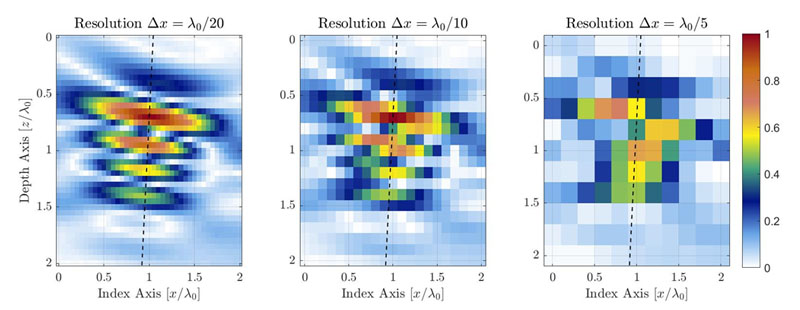
图1.降低TFM网格分辨率后导致TFM图像质量下降的图示。虚线代表声波传播的主轴。
对于相同的感兴趣区域来说,较低的网格分辨率将带来较少的像素数。图1显示了不同网格分辨率下同一侧钻孔(SDH)的典型TFM图像。网格分辨率的定义是探头中心频率波长的一部分λ0= c/f0,其中c是零件中的声波速度,而f0是探头的中心频率。
现在,标准和规范都要求振幅保真性不高于2 dB [1,10]。这一要求源于确保正确NDT分析的足够图像质量和检测效率之间的应用折衷,而后者的主要影响因子是给定感兴趣区域上TFM网格的密度。值得注意的是,TFM图像质量和检测效率之间的平衡对于没有强大处理能力的便携式独立设备来说尤其重要。随着嵌入式硬件功率效率的提高和远程计算的广泛应用,这一问题预计会随着时间推移而消失。
虽然已有一些经验方法[10-12],但其通常需要大量计算,且计算结果不能代表由网格分辨率导致的真实振幅。这一问题将在下一节中解释。本文提出了一种准确估计TFM设置下振幅保真性的方法,可帮助NDT技术人员高效、合规地进行TFM检测。
本文分为以下几部分。首先是全面解释了NDT技术人员面临的问题。随后介绍了一种测量TFM设置下振幅保真性的经验方法。然后建议了一个估计振幅保真性的分析模型,并通过三个不同的TFM用例来对比建议模型与经验测量值。最后是综述所完成工作的简要总结。
问题
虽然非常细(即致密)的网格能够实现极小的振幅保真性,但能够计算实时TFM图像的现代电子设备仍在计算方面受到限制。给定的感兴趣区域上较高的网格分辨率意味着需要计算大量的焦点,这会导致检测生产率和机械扫描速度下降。NDT技术人员必须能够选择正确的网格分辨率,才能够最大限度地提高检测生产率,并保持合规。
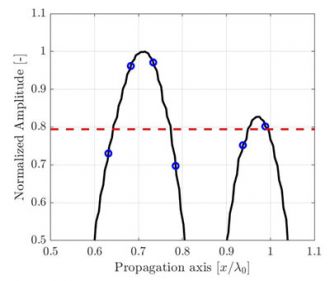
振幅保真性可用不同周期下的简单一维信号样本来说明。在图2的示例中显示的一维信号,是较高分辨率λ0/100下图1中SDH在声传播轴上的振幅。示例中仅呈现了接近信号最大振幅的放大部分。同样,三种不同分辨率λ0/20、λ0/10和λ0/5下的测量值,使用高分辨率插值参考线(纯黑色曲线)上的蓝色圆圈来标识。
(a) 离散网格分辨率是λ0/20,计算得出的振幅保真性是AF = 0.27dB。 |
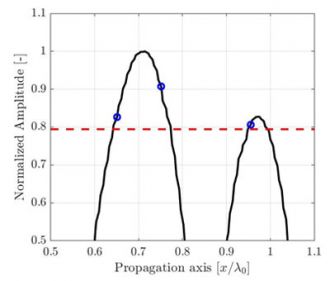
(b) 离散网格分辨率是λ0/10,计算得出的振幅保真性是AF = 0.82dB。 |
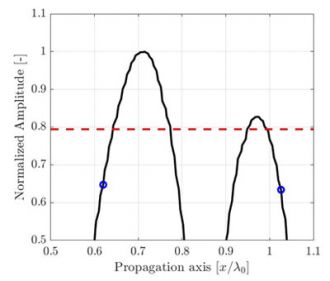
(c) 离散网格分辨率是λ0/5,计算得出的振幅保真性是AF = 3.7dB。 |
图2.采样周期对图1中传播轴上振幅记录值影响的图示。高分辨率插值信号参考线(黑线)仅供方便观察。红色虚线代表符合规范的振幅保真性2 dB。
由图可见,根据基于公式1量化的AF值,较密网格可以更好地表示连续信号,但仍存在优化问题:对于TFM图像上所有可能的网格位置来说,可以保证振幅保真性 等于目标值AFtarget的最大网格大小(Δxmax)是多少?或者
等于目标值AFtarget的最大网格大小(Δxmax)是多少?或者
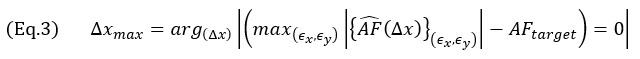
从这个问题的说明中可以清楚地看出,必须考虑基于位移(ϵx,ϵy)的所有网格平移,才能获得固定网格大小(Δx)的最大 。这样即可涵盖计算TFM图像时所有可能的网格安排。
。这样即可涵盖计算TFM图像时所有可能的网格安排。
下一节介绍了多个网格位移{ (Δx)}(ϵx,ϵy)产生一组振幅保真性的测量原理。
(Δx)}(ϵx,ϵy)产生一组振幅保真性的测量原理。
振幅保真性的经验测量
在介绍如何使用简单的分析模型估计振幅保真性之前,必须首先定义如何通过TFM图像、以实验方式测量振幅保真性。NDT行业中已经介绍并提出了几种技术[10-12],但其中一些技术并不能完全量化振幅保真性。振幅保真性的经验测量需要从多个精确的TFM网格位置计算大量TFM图像,因而很快便会成为NDT技术人员的采样负担。
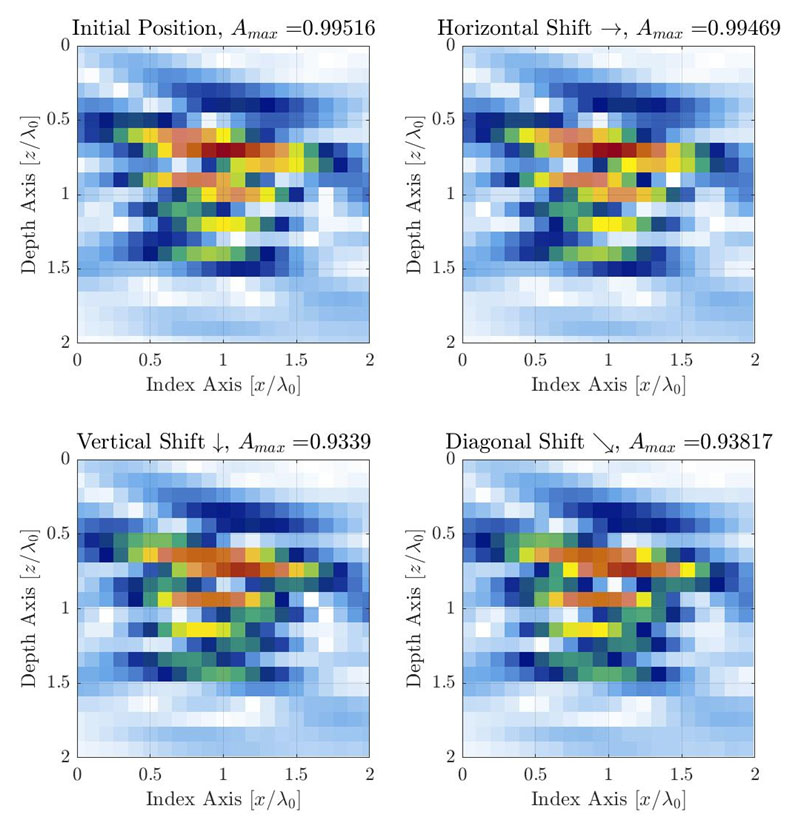
图3. 网格在3个不同方向上产生位移时,离散网格分辨率导致AF变化的图示。网格分辨率设置为Δx=Δy=λ0/10。网格分别向右(ϵx=λ0/40,ϵy=0)(右上)、向下(ϵx=0,ϵy=λ0/40)(左下)和沿对角线(ϵx=λ0/40,ϵy=λ0/40)(右下)偏移四分之一格。
在典型的TFM应用中,SDH是振幅校准和振幅保真性测量的参考缺陷[1,10]。观察到的振幅是感兴趣区域中的探头、楔块和目标位置(即相对于探头的TFM网格位置)的函数,沿声传播的主轴行进时变化最大。在图1的示例中,声传播的主轴几乎垂直。但对于一般测量方法来说,根据在感兴趣区域内的位置,传播轴不尽相同。在TFM图像中,采样网格必须在所有方向上移动才能采集到由离散网格导致的真实振幅变化。这一过程以图1示例(中间)为例在下图中说明,其中网格分辨率为λ0/10。
建议将网格在每个方向上移动待测试网格分辨率的一小部分(例如分辨率的二十分之一),移动次数取决于获得网格重叠所需的次数。这意味着在两个正交方向上覆盖一个网格分辨率的偏移时,总共需要202=400个位移步长(使用分辨率的二十分之一时的建议网格步长)。为每一网格偏移记录最大振幅,使用公式2,通过最大和最小记录值来获得振幅保真性。在图3的示例中,网格分辨率是λ0/10,且振幅保真性测量值是0.88 dB。考虑到所需的位移次数,这一手动过程对NDT技术人员来说既繁琐又耗时。这也意味着一共需要计算400幅TFM图像才能测量出单个网格分辨率的振幅保真性。
值得一提的是,使用TFM网格位置相对于探头的软件位移,而非ASME第五节[12]中提出的探头相对于零件的机械位移时,可利用一个单个FMC数据集生成多幅TFM图像。这种方法的另一个优势是能够读取网格的垂直分量。实际上,探头和楔块不能在深度轴上相对所选SDH以机械方式移动。
有些NDT设备实际上可提供用于移动TFM网格的半自动工具,并可记录感兴趣区域的最大振幅,从而最终计算产生的振幅保真性[11]。然而,这些工具通常只在水平方向上移动网格,因而会低估振幅保真性。相比之下,如果网格仅沿水平轴移动(例如图3),测得的振幅保真性仅为0.06 dB,与考虑垂直轴时相比低15倍以上。
振幅保真性估计的唯象模型
本节建议了一种基于经验观测值的简单分析模型。唯象模型考虑了沿传播主轴的信号行为,其中假设传播主轴包含大部分振幅波动,因而对网格分辨率最敏感。图4显示了一个SDH沿传播主轴(蓝色)和束腰轴(红色)的TFM图像的经验曲线。轴原点位于包络表示的视最大振幅位置,其解释了振荡沿轴 的小偏移。图中提供了标准振荡TFM和TFM包络的曲线。
的小偏移。图中提供了标准振荡TFM和TFM包络的曲线。
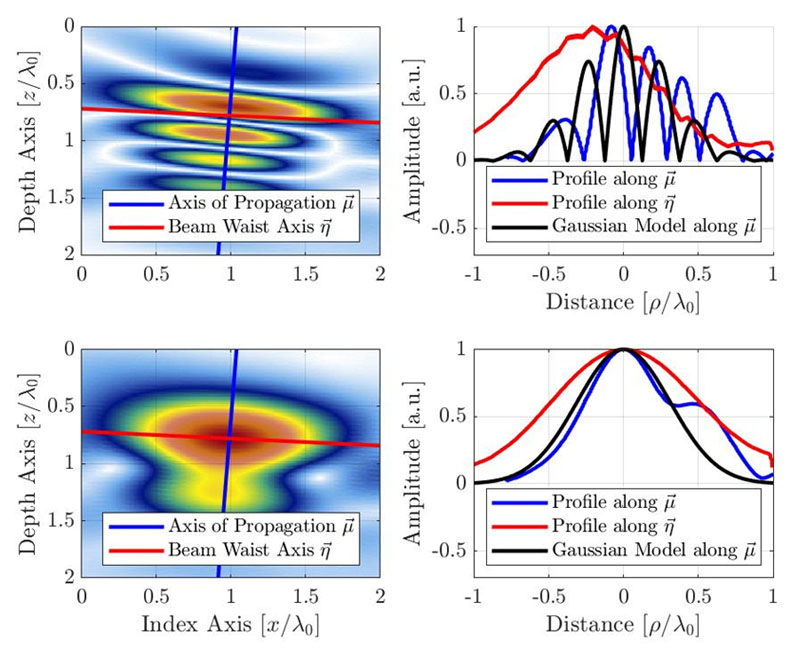
图4.TFM图像(顶部:振荡,底部:包络),包括沿声传播轴和束腰轴的信号曲线。此外还显示了振荡和包络TFM图像的建议高斯模型。需注意的是,视波长因TFM波束成形的脉冲回波性质而减半。
如前所述,假设振幅变化最大的轴是声传播的主轴。因此,模型旨在再现该方向上的振幅变化。模型信号是余弦调制的高斯信号
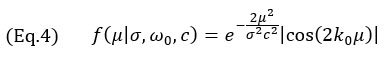
其中k0=ω0/c是探头中心角频率ω0的波数,σ是取决于中心频率和相对波长bw的宽度参数。宽度参数σ的计算公式为
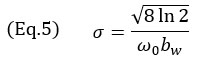
对于典型的NDT相控阵探头,相对带宽接近60%,因此在模型中使用(bw=0.6)的数值。这反过来使高斯包络大于单个余弦振荡。值得一提的是,公式3中余弦项的中心频率是探头中心频率的两倍。这是由于TFM成像(发射和接收路径)的脉冲回波性质,且可在图4振荡间的距离中观察到。事实上,时域和空间域之间的转换写为μ = tc/2。这也解释了公式3中指数项使用的系数2。
在公式4的振荡模型中,高斯包络比余弦函数的单个振荡大得多,而较大的值会产生AF的空间假频,因此只考虑|μ|≤λ0/8的数值。
对于TFM包络模型,仅使用公式4的高斯项生成以下公式
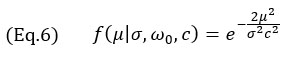
对任何网格分辨率均有效。图4显示了使用公式3和7模型获得的曲线以及实验曲线。需注意的是,经验测量也会显示滞后于主回波的表面波信号(SDH典型的“环绕”回波),而这一特征在建议的模型中明显缺失。
为了获得模型的振幅保真性的最坏情况,必须考虑缺陷相对于网格正交轴的方向。如图5a所示,当声传播的主轴 平行于网格轴之一时,会出现振荡TFM的最坏情况。因此,必须在最大振幅位于沿
平行于网格轴之一时,会出现振荡TFM的最坏情况。因此,必须在最大振幅位于沿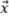 或
或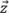 轴的两个网格点之间的假设下计算振幅保真性,从而得到
轴的两个网格点之间的假设下计算振幅保真性,从而得到
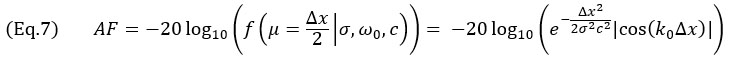
用于Δx≤λ0/4。对于TFM包络来说,当传播主轴 和束腰轴
和束腰轴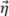 上的振幅曲线相同时才会出现最坏情况。图5b中示例对应于以圆表示的SDH,因此传播主轴
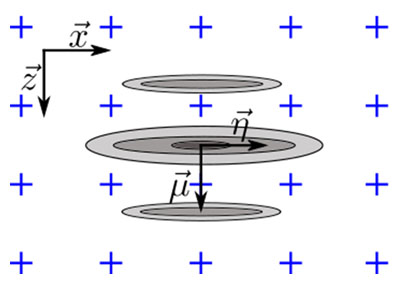
上的振幅曲线相同时才会出现最坏情况。图5b中示例对应于以圆表示的SDH,因此传播主轴 可有任何方向。最坏情况在SDH回波位于四个相邻点之间中心时出现,如图所示。此时,必须沿着网格对角线计算振幅保真性,才能有效地得到
可有任何方向。最坏情况在SDH回波位于四个相邻点之间中心时出现,如图所示。此时,必须沿着网格对角线计算振幅保真性,才能有效地得到
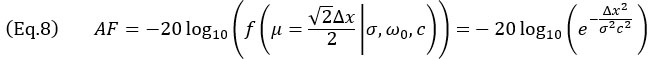
在AF值较小时(即NDT应用的典型使用情况),可为公式7的振荡模型获得相对于AF的Δx近似值,

以及为公式8的包络模型获得
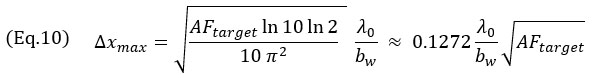
这些表达式在所有情况下都会转换网格大小平方根对AF值的依赖性。公式9由公式7的二阶泰勒级数近似后获得。图6中显示了近似值与精确模型。此外需注意的是,振荡模型的网格大小几乎独立于小bw相对带宽。还需注意的是,振荡和包络模型中的最大网格分辨率Δxmax与目标振幅保真性的平方根相关。这些值代表唯象模型的合规最大网格分辨率。
(a) 轴 |
(b) 振幅曲线沿 |
图5.(a)振荡TFM和(b)TFM包络最坏情况下缺陷相对于网格正交轴方向的图示。
实验验证
通过三个不同的TFM检测用例的经验测量值来验证建议模型。在这三个TFM设置下,以不同的网格分辨率对几个SDH成像,然后使用前述方法测量振幅保真性。这三个用例的参数如表1所示。第一个用例是与高频探头(7.5 MHz)接触,第二个使用了较低频率(5 MHz)的剪切波,第三个则使用了较高探头频率(10 MHz)下的剪切波和元素计数。在所有三个用例中,SDH都在距离碳钢块顶面50 mm以内。
表1:用于振幅保真性实验验证的TFM设置的参数。
| 用例 | 探头参数 | 楔块参数 | 零件参数 | TFM模式 | |||||
|---|---|---|---|---|---|---|---|---|---|
|
频率
[MHz] |
数量
[#] |
间距
[mm] |
速度
[m/s] |
角度
[°] |
高度
[mm] |
速度
cp - cs [m/s] |
SDH
直径 [mm] | ||
| 1 | 7.5 | 64 | 1.0 | 不适用 | 不适用 | 0 | 3240 - 5890 | 1 | L-L |
| 2 | 5 | 32 | 1.0 | 2330 | 36.1 | 11.0 | 3240 - 5890 | 0.5 | T-T |
| 3 | 10 | 64 | 0.5 | 2330 | 36.1 | 11.0 | 3240 - 5890 | 1 | T-T |
图5显示了标准振荡TFM(顶部)和TFM包络(底部)的振幅保真性。每个灰点代表用例、SDH和网格分辨率的不同组合。纯黑色曲线代表使用前述高斯模型估计的振幅保真性。红色虚线代表合规的2 dB限值。
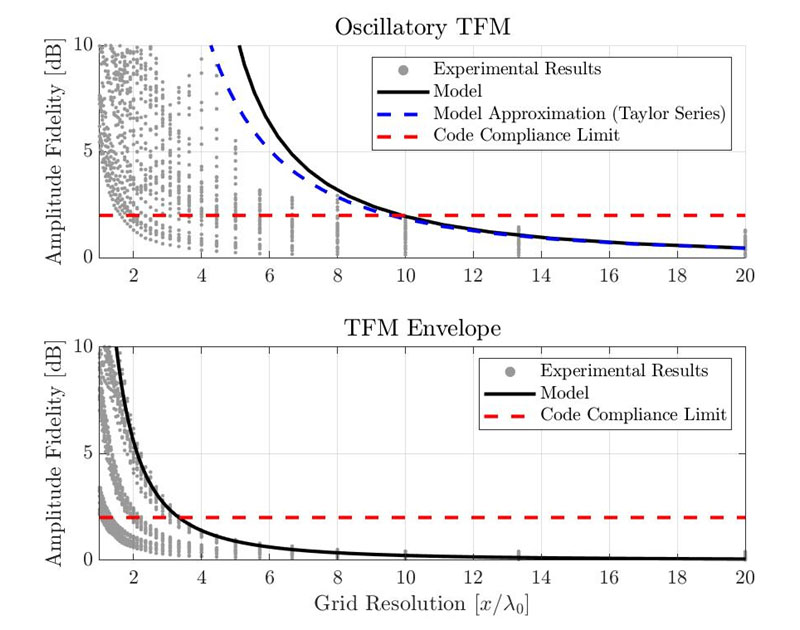
图6.标准振荡TFM(顶部)和TFM包络(底部)的经验振幅保真性测量值与建议高斯模型结果之间的对比。
根据建议的模型,振荡TFM所需的合规分辨率为λ0/9.9,而TFM包络为λ0/3.3。经验结果显示,标准振荡TFM所需的合规分辨率为λ0/10,而TFM包络为λ0/3.3。但需注意的是,以上数值取自所示的最差实验情况。即使在较低网格分辨率下,部分振幅保真性测量值也低于2 dB。因此,建议的模型为TFM设置的振幅保真性提供了良好但保守的估计。
结语
TFM设置的振幅保真性是相对于网格分辨率的成像可靠性的重要衡量指标。网格越密,振幅保真性值就越小。目前,规范和标准已纳入作为新检测技术的全聚焦方式,并且要求振幅保真性值在2 dB或以下。本文介绍了如何以经验方式正确测量振幅保真性,并提出了一个简单的分析模型来估计TFM设置结果的振幅保真性。
这一简单分析模型基于沿声传播主轴的振幅曲线。模型通过高斯调制余弦振荡来估计振幅曲线。使用此曲线估计振幅保真性可为标准振荡TFM和TFM包络两者都获得很好的结果。经验值显示标准振荡TFM和TFM包络分别需要最高λ0/10或λ0/3.3的网格分辨率。建议模型估计的标准TFM的网格分辨率为λ0/9.9,而TFM包络为λ0/3.3。因此,可使用建议模型估计TFM设置的振幅保真性。
有关合规解决方案中TFM包络优势的详细信息,请阅读白皮书“使用带包络特征的全聚焦方式”。
参考文献
[1] ASME Committee, 2019, “ASME BPVC.V Article 4 Mandatory Appendix XI Full Matric Capture.”
[2] Oralkan, O., Ergun, A. S.,Johnson, J. A., Karaman, M., Demirci, U., Kaviani, K., Lee, T. H., and Khuri-Yakub, B. T., 2002, “Capacitive Micromachined Ultrasonic Transducers: Next-Generation Arrays for Acoustic Imaging?,” IEEE Trans. Ultrason.,Ferroelect., Freq.Contr., 49(11), pp. 1596–1610.
[3] Thomenius, K. E., 1996, “Evolution of Ultrasound Beamformers,” 1996 IEEE Ultrasonics Symposium. Proceedings, IEEE, San Antonio, TX, USA, pp. 1615–1622.
[4] Freeman, S., Li, P.,and O’Donnell, M., “Retrospective Dynamic Transmit Focusing,” p. 24.
[5] Wilcox, P. D., 2006, “Exploiting the Full Data Set from Ultrasonic Arrays by Post-Processing,” AIP Conference Proceedings, AIP, Brunswick, Maine (USA), pp. 845–852.
[6] Portzgen, N., Gisolf, D., and Blacquiere, G., 2007, “Inverse Wave Field Extrapolation: A Different NDI Approach to Imaging Defects,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 54(1), pp. 118–127.
[7] Sharpe, R. S.,ed., 1982, Research Techniques in Nondestructive Testing. Vol. 6: ..., Acad. Press, London.
[8] Holmes, C., Drinkwater, B. W., and Wilcox, P. D., 2008, “Advanced Post-Processing for Scanned Ultrasonic Arrays: Application to Defect Detection and Classification in Non-Destructive Evaluation,” Ultrasonics, 48(6–7), pp. 636–642.
[9] Holmes, C., Drinkwater, B. W., and Wilcox, P. D., 2005, “Post-Processing of the Full Matrix of Ultrasonic Transmit–Receive Array Data for Non-Destructive Evaluation,” NDT & E International, 38(8), pp. 701–711.
[10] ISO, 2020, “ISO/DIS 23865 -FMC-TFM - General Use of TFM-FMC Technique.”
[11] Johnson, P., 2019, “With a New Software Wizard, There’s No Sorcery but the Magic of the M2M Gekko Is Evident with Instant Code Compliance for Your TFM Weld Inspections.,” Code Compliant TFM Weld Inspection with Three Clicks.
[12] ASME Committee, 2019, “ASME BPVC.V Article 4 Nonmandatory Appendix F - Examination of Welds Using Full Matrix Capture.”