Autores: Nicolas Badeau, Guillaume Painchaud-April e Chi-Hang Kwan
Resumo
A técnica de inspeção de método de foco total (total focusing method, TFM) agora está incluída nos códigos e normas que regulamentam os ensaios não destrutivos (END), como a Seção V da ASME. Um parâmetro importante especificado nesses códigos para o planejamento do rastreamento com TFM é a fidelidade da amplitude. Ela é definida como a variação da amplitude obtida de um refletor especificado, devido à resolução finita da grade de formação de imagem. O limiar típico de fidelidade da amplitude admissível nesses códigos é de no máximo 2 dB. Embora os códigos sugiram métodos experimentais para medir a fidelidade da amplitude de uma determinada configuração, um método analítico simples e conservador é proposto neste artigo. O uso do envelope de TFM também é considerado na estimativa da fidelidade da amplitude, uma vez que permite que uma grade de TFM menos densa seja usada sem fazer com que o valor de fidelidade da amplitude exceda a tolerância estabelecida. Para a formação de imagem do TFM padrão, os resultados empíricos demonstraram que é necessária uma resolução da grade de aproximadamente λ0/10 para obter uma fidelidade da amplitude inferior a 2 dB. Para a formação de imagem do TFM com o envelope, os resultados empíricos demonstraram a necessidade de uma resolução da grade de λ0/3,3 para estar em conformidade com o código.
Introdução
O método de foco total (TFM) é uma técnica recentemente aceita para ensaios não destrutivos (END) de componentes. As normas e os códigos, como a ASME V [1], integraram a captação integral de matriz (full matrix capture, FMC) e o TFM como uma técnica adicional de inspeção ultrassônica phased array. Embora a FMC/TFM seja relativamente nova na indústria de END, ela tem sido usada por algum tempo em aplicações médicas como o padrão-ouro da formação de imagens médicas de ultrassom [2–4]. De fato, a maioria das técnicas de formação de imagens médicas de ultrassom normalmente é referenciada e comparada com a formação de imagem do TFM.
Embora existam várias técnicas semelhantes à FMC/TFM (por ex., VTFM [5], IWEX [6], SAFT [7]), o algoritmo mais comumente usado é o processamento de atraso e soma [2–4, 8, 9]. A técnica FMC/TFM consiste em um esquema de aquisição (FMC), que conta com a aquisição do sinal de todas as combinações dos elementos do transmissor e do receptor, e um esquema de soma (TFM), que calcula o resultado do feixe ultrassônico focalizado em vários locais em uma região de interesse. A região de interesse do TFM muitas vezes é representada em um plano cartesiano, e as interseções individuais do plano no qual a focalização acústica é aplicada são chamadas de pixels. O método de focalização é semelhante à formação de imagem de ultrassom phased array, exceto pelo fato de que os feixes são formados no pós-processamento usando os dados armazenados na matriz de dados FMC. O processo de atraso e soma da pós-aquisição assume a linearidade das ondas acústicas subjacentes encontradas em aplicações de END típicas.
A técnica FMC/TFM pode ser vista como uma extensão natural da técnica de phased array convencional. No entanto, novos parâmetros de configuração devem ser considerados devido às diferenças na representação dos dados em comparação com os testes de ultrassom phased array (phased array ultrasonic testing, PAUT) convencionais. Um desses conceitos é a fidelidade da amplitude (amplitude fidelity, AF) de uma grade de TFM. A AF é definida como a variação máxima da amplitude de uma indicação causada pela resolução da grade de TFM {Δx,Δz}. O uso de um plano cartesiano uniforme, ou seja, (Δx=Δz), é considerado para o restante deste estudo. A fidelidade da amplitude pode ser formalmente expressa como
![(Eq.1) AF(Δx)≡-20 log〖(A_(máx. amostrado) (Δx))/A_(máx. verdadeiro) 〗 [dB]](https://industrial.evidentscientific.com.cn/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_01.jpg?rev=43A1)
onde Amáx. amostrado é a amplitude máxima medida de uma característica de interesse com base em uma amostragem de grade finita, e Amáx. verdadeiro é o máximo da mesma característica de interesse com base em uma resolução de grade infinita. O limite no qual o tamanho da grade se torna zero nos dois eixos para Amáx. amostrado (Δx) define o Amáx. verdadeiro, e a fidelidade da amplitude correspondente se torna 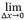 AF(Δx)=0. A Equação 1 fornece uma definição formal para calcular a fidelidade da amplitude em relação à resolução da grade. No entanto, na prática, o máximo verdadeiro Amáx. verdadeiro do sinal subjacente somente pode ser estimado por meio de uma superamostragem da imagem de amplitude do TFM e interpolação,
AF(Δx)=0. A Equação 1 fornece uma definição formal para calcular a fidelidade da amplitude em relação à resolução da grade. No entanto, na prática, o máximo verdadeiro Amáx. verdadeiro do sinal subjacente somente pode ser estimado por meio de uma superamostragem da imagem de amplitude do TFM e interpolação,
![(Eq.2) (AF) ̂(Δx)=-20 log〖(A_(máx. amostrado) (Δx))/A ̂_(máx. verdadeiro) 〗 [dB]](https://industrial.evidentscientific.com.cn/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_02.jpg?rev=43A1)
onde  máx. verdadeiro é um estimador do Amáx. verdadeiro
máx. verdadeiro é um estimador do Amáx. verdadeiro
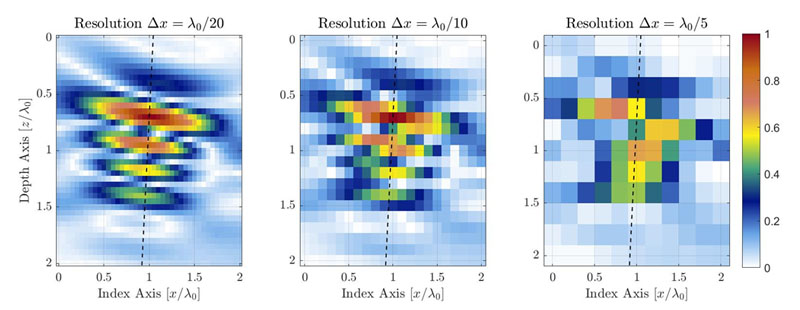
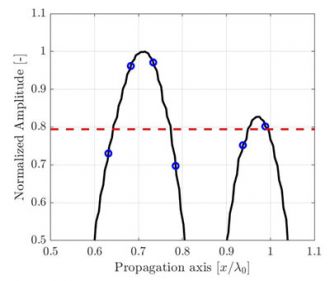
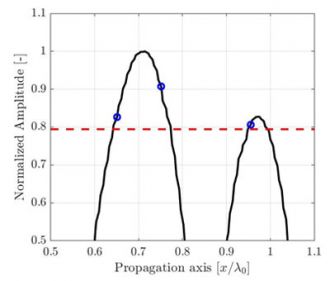
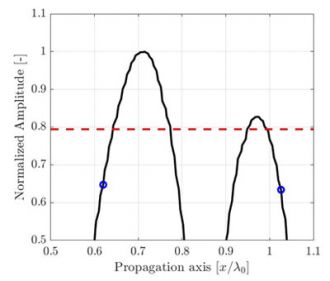
Figura 1. Ilustração da degradação da qualidade da imagem do TFM causada pela diminuição da resolução da grade de TFM. As linhas tracejadas representam o eixo principal de propagação acústica.
Para uma zona de interesse idêntica, uma resolução da grade menos precisa terá uma contagem de pixels menor. A Figura 1 mostra imagens do TFM típicas do mesmo orifício lateral perfurado (side-drilled hole, SDH) com diferentes valores de resolução da grade. A resolução da grade é definida como uma fração do comprimento de onda da frequência central da sonda λ0= c/f0, onde c é a velocidade acústica na peça e f0 é a frequência central da sonda.
As normas e códigos agora incluem um requisito de que a fidelidade da amplitude seja no máximo 2 dB [1, 10]. Este requisito surge do comprometimento de aplicação entre uma qualidade de imagem suficiente para garantir uma análise de END adequada e a produtividade da inspeção, que é extremamente impactada pela densidade da grade de TFM em uma determinada região de interesse. Observe que o equilíbrio entre a qualidade da imagem do TFM e a produtividade da inspeção é especialmente crítico para dispositivos portáteis autônomos que não têm acesso a uma grande capacidade de processamento. Espera-se que este problema desapareça com o tempo, conforme a eficiência da capacidade do hardware integrado melhora e o cálculo remoto se torna amplamente disponível.
Embora alguns métodos empíricos tenham sido propostos [10–12], eles normalmente requerem um cálculo extenso e os resultados obtidos não são representativos da amplitude verdadeira causada pela resolução da grade, um problema que será explicado na seção a seguir. Este artigo apresenta um método para estimar de forma precisa a fidelidade da amplitude de uma configuração de TFM para ajudar os técnicos de END a realizarem uma inspeção com TFM produtiva e em conformidade com o código.
Este artigo está dividido da seguinte forma. Primeiro, é apresentada uma explicação abrangente do problema enfrentado pelos técnicos de END. Depois, é descrito um método para medir empiricamente a fidelidade da amplitude de uma configuração de TFM. Na seção seguinte, é proposto um modelo analítico para estimar a fidelidade da amplitude. Em seguida, o modelo proposto é comparado com as medições empíricas em três casos de uso do TFM diferentes. É apresentada uma breve conclusão abordando o trabalho realizado.
Problemática
Embora uma grade muito precisa (ou seja, densa) permita uma fidelidade da amplitude muito pequena, os dispositivos eletrônicos atuais capazes de calcular imagens do TFM em tempo real ainda possuem limites computacionais. Uma resolução de grade mais precisa em uma determinada região de interesse significa que existe um grande número de pontos de focalização para calcular, resultando em uma diminuição da produtividade da inspeção e da velocidade de rastreamento mecânico. O técnico de END deve ser capaz de selecionar uma resolução de grade apropriada que maximize a produtividade da inspeção mantendo ao mesmo tempo a conformidade com o código.
A fidelidade da amplitude pode ser ilustrada com uma amostra de sinal unidimensional simples em vários períodos. No exemplo mostrado na Figura 2, o sinal unidimensional apresentado é a amplitude do SDH apresentado na Figura 1 ao longo do eixo de propagação acústica, obtido de uma imagem λ0/100 de alta resolução. Somente uma parte amplificada, próxima da amplitude máxima do sinal, é apresentada para efeitos do exemplo. Novamente, as medições em três resoluções diferentes λ0/20, λ0/10, e λ0/5, são identificadas pelos círculos azuis sobre uma referência interpolada de alta resolução (curva preta simples).
(a) A resolução discreta da grade é λ0/20 e a fidelidade da amplitude calculada é AF = 0,27 dB. |
(b) A resolução discreta da grade é λ0/10 e a fidelidade da amplitude calculada é AF = 0,82 dB. |
(c) A resolução discreta da grade é λ0/5 e a fidelidade da amplitude calculada é AF = 3,7 dB. |
Figura 2. Ilustração do efeito do período de amostragem na amplitude registrada ao longo do eixo de propagação representado na Fig. 1. Uma referência de sinal interpolado de alta resolução (linha preta) é ilustrada para auxiliar a visualização. A fidelidade da amplitude em conformidade com o código de 2 dB é representada por uma linha vermelha tracejada.
A conclusão óbvia é que uma grade mais densa fornece uma melhor representação de um sinal contínuo, conforme quantificado pelo valor de AF da Equação 1, mas o problema de otimização permanece: qual é o tamanho máximo da grade (Δxmáx.) que garante, para todas as posições de grade possíveis em uma imagem do TFM, uma fidelidade de amplitude  que seja igual a um valor-alvo AFalvo? Ou,
que seja igual a um valor-alvo AFalvo? Ou,
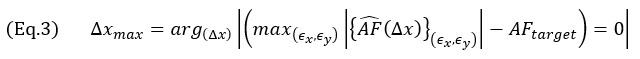
É claro, a partir dessa descrição do problema, que todas as translações da grade, identificadas por deslocamentos (ϵx,ϵy), devem ser levadas em consideração para obter a  máxima para um tamanho da célula fixo (Δx). O objetivo disso é incluir todos os casos possíveis de posicionamentos na grade para calcular a imagem do TFM.
máxima para um tamanho da célula fixo (Δx). O objetivo disso é incluir todos os casos possíveis de posicionamentos na grade para calcular a imagem do TFM.
Na seção a seguir, é fornecida uma ilustração do princípio de medição para o conjunto de valores de fidelidade da amplitude produzidos a partir de vários deslocamentos da grade{ (Δx)}(ϵx,ϵy).
(Δx)}(ϵx,ϵy).
Medição empírica da fidelidade da amplitude
Antes de apresentar como a fidelidade da amplitude pode ser estimada usando um modelo analítico simples, é muito importante definir como medi-la experimentalmente no caso de uma imagem do TFM. Várias técnicas foram descritas e propostas na indústria de END [10–12], mas algumas delas não quantificam a fidelidade da amplitude de uma forma completa. A medição empírica da fidelidade da amplitude pode rapidamente tornar-se um fardo na aquisição para o técnico de END, pois requer o cálculo de um grande número de imagens do TFM a partir de várias posições precisas da grade de TFM.
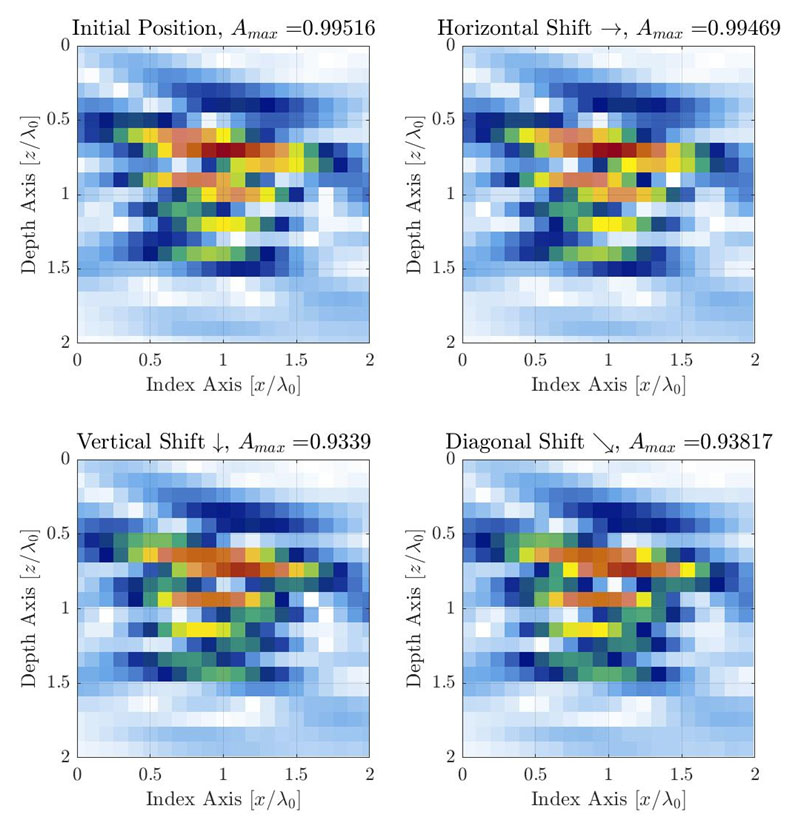
Figura 3. Ilustração da variação de AF causada pela resolução discreta da grade conforme a grade é deslocada em 3 direções diferentes. A resolução da grade está definida como Δx=Δy=λ0/10. A grade é deslocada em um quarto da célula da grade à direita (ϵx=λ0/40,ϵy=0) (em cima à direita), embaixo (ϵx=0,ϵy=λ0/40) (embaixo à esquerda) e diagonalmente (ϵx=λ0/40,ϵy=λ0/40) (embaixo à direita).
Para aplicações do TFM típicas, um SDH é usado como um defeito de referência para a calibração da amplitude e para a medição da fidelidade da amplitude [1, 10]. A amplitude observada terá uma maior variação ao longo do eixo principal de propagação acústica, que é uma função da sonda, calço e posição do alvo na região de interesse (ou seja, a posição da grade de TFM em relação à sonda). No caso ilustrado na Figura 1, o eixo principal de propagação é quase vertical. No entanto, para um método de medição genérico, o eixo de propagação será diferente dependendo da localização dentro da região de interesse. Para uma imagem do TFM, a grade de amostragem deve ser movida em todas as direções para capturar a variação da amplitude verdadeira causada pela grade discreta. Este processo é ilustrado abaixo com o mesmo exemplo da Figura 1 (central), que tem uma resolução da grade de λ0/10.
É sugerido mover a grade em uma fração da resolução da grade para que seja testada (por exemplo, cerca de um vigésimo da resolução) em todas as direções quantas vezes for necessário para obter uma sobreposição da grade. Isso significa que, para abranger um desvio de uma resolução da grade nas duas direções ortogonais, é necessário um total de 202 = 400 incrementos de deslocamento (se estiver usando o incremento de grade sugerido de um vigésimo da resolução). A amplitude máxima é registrada para todos os desvios da grade, e os valores máximo e mínimo registrados são usados para obter a fidelidade da amplitude usando a Equação 2. No caso apresentado na Figura 3, a resolução da grade é λ0/10 e a fidelidade da amplitude medida é de 0,88 dB. A julgar pelo número de deslocamentos necessários, esse processo manual seria trabalhoso e demorado para o técnico de END. Isso também implica o cálculo de um total de 400 imagens do TFM para medir a fidelidade da amplitude de uma única resolução da grade.
Vale a pena mencionar que, ao usar o deslocamento do software da posição da grade de TFM em relação à sonda em vez de um deslocamento mecânico da sonda em relação à peça conforme proposto na Seção V da ASME [12], várias imagens do TFM podem ser geradas usando um único conjunto de dados de FMC. Outro benefício desta abordagem é a capacidade de acessar o componente vertical da grade. De fato, a sonda e o calço não podem ser movidos mecanicamente em relação ao SDH selecionado ao longo do eixo de profundidade.
Alguns dispositivos de END disponibilizam ferramentas semiautomatizadas que deslocam a grade de TFM, registram a amplitude máxima na região de interesse e, finalmente, calculam a fidelidade da amplitude resultante [11]. No entanto, essas ferramentas geralmente somente deslocam a grade na direção horizontal e, consequentemente, subestimam a fidelidade da amplitude. Para efeitos de comparação, se a grade for movida somente ao longo do eixo horizontal, por exemplo, como ilustrado na Figura 3, a fidelidade da amplitude medida é de 0,06 dB, o que é mais de 15 vezes inferior à fidelidade da amplitude medida considerando o eixo vertical.
Um modelo fenomenológico para a estimativa da fidelidade da amplitude
Esta seção propõe um modelo analítico simples baseado na observação empírica. O modelo fenomenológico considera o comportamento do sinal ao longo do eixo principal de propagação, que presume-se conter a maioria das flutuações de amplitude e, portanto, ser o mais sensível à resolução da grade. A Figura 4 mostra o perfil empírico de uma imagem do TFM resultante de um SDH ao longo do eixo principal de propagação (azul) e ao longo do eixo central do feixe (vermelho). A origem do eixo está localizada no local aparente de amplitude máxima da representação de envelope, o que explica o pequeno desvio ao longo do eixo  para a representação da oscilação. Os perfis do TFM oscilatório padrão e do envelope do TFM são fornecidos.
para a representação da oscilação. Os perfis do TFM oscilatório padrão e do envelope do TFM são fornecidos.
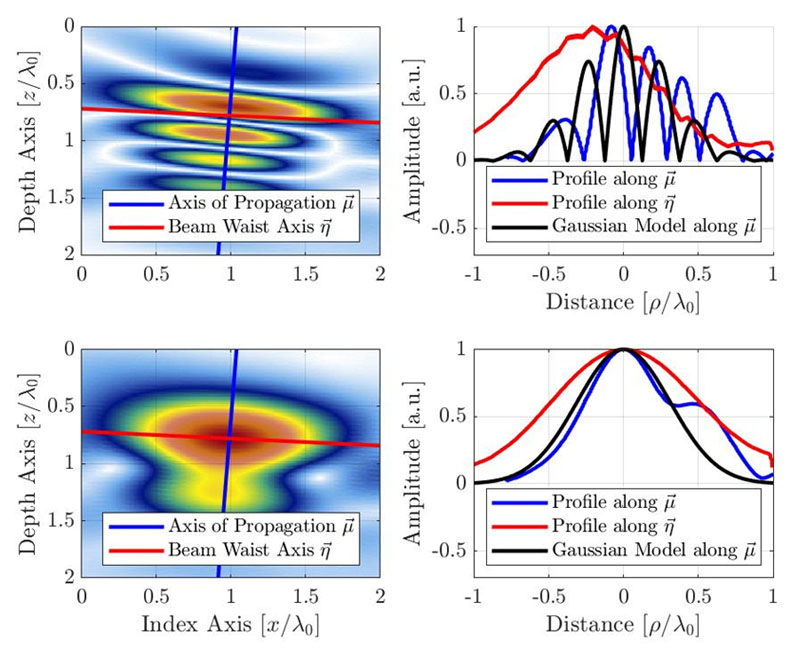
Figura 4. Imagem do TFM (em cima: oscilatório, embaixo: envelope) com o perfil do sinal ao longo do eixo de propagação acústica e do eixo central do feixe. O modelo gaussiano proposto também é ilustrado para as imagens do TFM oscilatório e de envelope. Observe que o comprimento de onda aparente é reduzido pela metade devido à natureza de pulso-eco da formação de feixe de TFM.
Como indicado anteriormente, presume-se que o eixo com a maior variação de amplitude seja ao longo do eixo principal de propagação acústica. Assim, o modelo tem o objetivo de reproduzir a variação da amplitude nessa direção. O sinal do modelo é um gaussiano modulado por cosseno
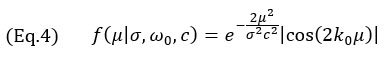
onde k0=ω0/c é o número de onda na frequência angular central ω0 da sonda, σ é o parâmetro de largura dependente da frequência central e da largura de banda relativa bw. O parâmetro de largura σ é calculado usando
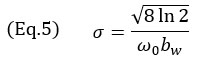
Para uma sonda phased array de END típica, a largura de banda relativa é próxima do marco de 60%, por isso, um valor de (bw=0,6) é usado no modelo. Isso, por sua vez, torna o envelope gaussiano maior do que uma única oscilação de cosseno. Vale a pena mencionar que a frequência central do termo do cosseno na Equação 3 é duplicada a partir da frequência central da sonda. Isso ocorre devido à natureza de pulso-eco da formação de imagem do TFM (trajetória de transmissão e recebimento) e é possível observar na distância entre as oscilações na Figura 4. Na verdade, a conversão entre o domínio de tempo e o domínio de espaço é descrita como μ = tc/2. Isso também explica o fator 2 usado como termo exponencial da Equação 3.
Para o modelo oscilatório da Equação 4, uma vez que o envelope gaussiano é muito maior do que uma única oscilação da função do cosseno, somente os valores |μ|≤λ0/8 são considerados, pois valores maiores produzem um aliasing espacial para a AF.
Para o modelo de envelope de TFM, somente o termo gaussiano da Equação 4 é usado, produzindo o seguinte
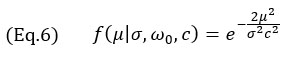
que é válida para qualquer resolução da grade. O perfil obtido com o modelo das Equações 3 e 7 é ilustrado na Figura 4 junto com os perfis experimentais. Observe que as medições empíricas também mostram o sinal da onda de superfície (o eco "enrolado" típico dos SDHs) atrasado em relação ao eco principal, uma característica perceptivelmente ausente no modelo proposto.
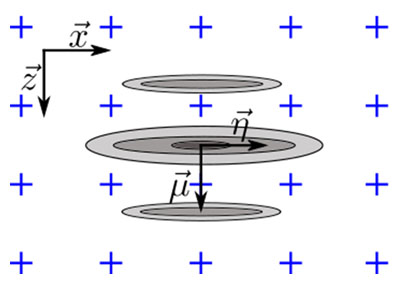
A orientação do defeito em relação aos eixos ortogonais da grade deve ser considerada para obter o pior caso de fidelidade da amplitude com o modelo. Conforme ilustrado na Figura 5a, o pior caso para o TFM oscilatório ocorre quando o eixo principal de propagação acústica  está paralelo a um dos eixos da grade. Consequentemente, a fidelidade da amplitude deve ser calculada como se a amplitude máxima estivesse centralizada entre dois pontos da grade ao longo de qualquer eixo
está paralelo a um dos eixos da grade. Consequentemente, a fidelidade da amplitude deve ser calculada como se a amplitude máxima estivesse centralizada entre dois pontos da grade ao longo de qualquer eixo 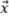 ou
ou 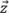 , produzindo
, produzindo
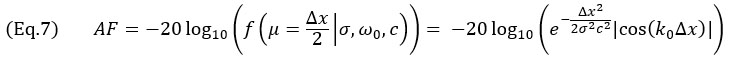
para Δx≤λ0/4. Para o envelope de TFM, o pior caso ocorre quando o perfil da amplitude é idêntico ao longo do eixo principal de propagação  e do eixo central do feixe
e do eixo central do feixe 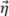 . Esse caso, ilustrado na Figura 5b, corresponde a quando o SDH é representado como um círculo, e, por isso, o eixo principal de propagação
. Esse caso, ilustrado na Figura 5b, corresponde a quando o SDH é representado como um círculo, e, por isso, o eixo principal de propagação  pode ter qualquer orientação. O pior caso ocorre quando o eco do SDH está centralizado entre quatro pontos adjacentes, como ilustrado. Nesse caso, a fidelidade da amplitude deve ser calculada ao longo da diagonal da grade, produzindo efetivamente
pode ter qualquer orientação. O pior caso ocorre quando o eco do SDH está centralizado entre quatro pontos adjacentes, como ilustrado. Nesse caso, a fidelidade da amplitude deve ser calculada ao longo da diagonal da grade, produzindo efetivamente
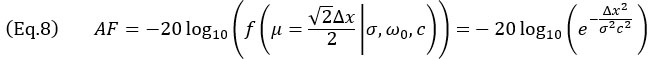
Uma forma aproximada do valor de Δx em relação à AF, nos casos em que o valor de AF é pequeno, que é o caso de uso típico para aplicações de END, pode ser obtida para o modelo oscilatório da Equação 7,

e para o modelo de envelope da Equação 8,
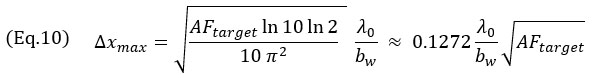
Essas expressões traduzem a dependência da raiz quadrada do tamanho da grade no valor de AF em todos os casos. A Equação 9 foi obtida usando a aproximação da série de Taylor de segunda ordem da Equação 7. Essa aproximação está ilustrada na Figura 6 junto com o modelo exato. Além disso, observe que o tamanho da grade para o modelo oscilatório é quase independente da largura de banda relativa para um bw pequeno. Também vale a pena mencionar que, para os modelos oscilatório e de envelope, a resolução máxima da grade Δxmáx. está relacionada à raiz quadrada da fidelidade da amplitude alvo. Esses valores representam a resolução máxima da grade para a conformidade com o código com base no modelo fenomenológico.
(a) O pior caso para o TFM oscilatório ocorre quando o eixo |
(b) O pior caso para o envelope de TFM ocorre quando o perfil da amplitude ao longo de |
Figura 5. Ilustração da orientação do defeito em relação ao eixo ortogonal da grade para o pior caso, para (a) o TFM oscilatório e para (b) o envelope de TFM.
Validação experimental
O modelo proposto foi validado com os resultados empíricos em três casos de uso diferentes de inspeção com TFM. Para todas as três configurações de TFM, foram formadas imagens de vários SDHs com várias resoluções de grade e a fidelidade da amplitude foi medida usando o método descrito anteriormente. Os parâmetros dos três casos de uso estão descritos na Tabela 1. O primeiro caso é em contato com uma sonda de alta frequência (7,5 MHz), o segundo caso de uso emprega ondas de cisalhamento a uma baixa frequência (5 MHz) e o terceiro caso de uso emprega ondas de cisalhamento a uma frequência da sonda maior (10 MHz) e contagens de elementos. Em todos os casos, os SDHs estão localizados a menos de 50 mm da superfície superior de um bloco de aço carbono.
Tabela 1: Parâmetros das configurações de TFM usados para a validação experimental da fidelidade da amplitude.
| Caso | Parâmetros da sonda | Parâmetros do calço | Parâmetros da peça | Modo de TFM | |||||
|---|---|---|---|---|---|---|---|---|---|
|
Frequência
[MHz] |
Número
[#] |
Pitch
[mm] |
Velocidade
[m/s] |
Ângulo
[°] |
Altura
[mm] |
Velocidade
cp - cs [m/s] |
Diâmetro
do SDH [mm] | ||
| 1 | 7,5 | 64 | 1,0 | n/a | n/a | 0 | 3240 - 5890 | 1 | L-L |
| 2 | 5 | 32 | 1,0 | 2.330 | 36,1 | 11,0 | 3240 - 5890 | 0,5 | T-T |
| 3 | 10 | 64 | 0,5 | 2.330 | 36,1 | 11,0 | 3240 - 5890 | 1 | T-T |
A Figura 5 mostra a fidelidade da amplitude resultante para o TFM oscilatório padrão (em cima) e para o envelope de TFM (embaixo). Cada ponto cinza individual representa uma combinação diferente do caso de uso, SDHs e resolução da grade. A fidelidade da amplitude estimada usando o modelo gaussiano apresentado anteriormente é mostrada com uma curva preta simples. A linha vermelha tracejada representa o limite de conformidade com o código de 2 dB.
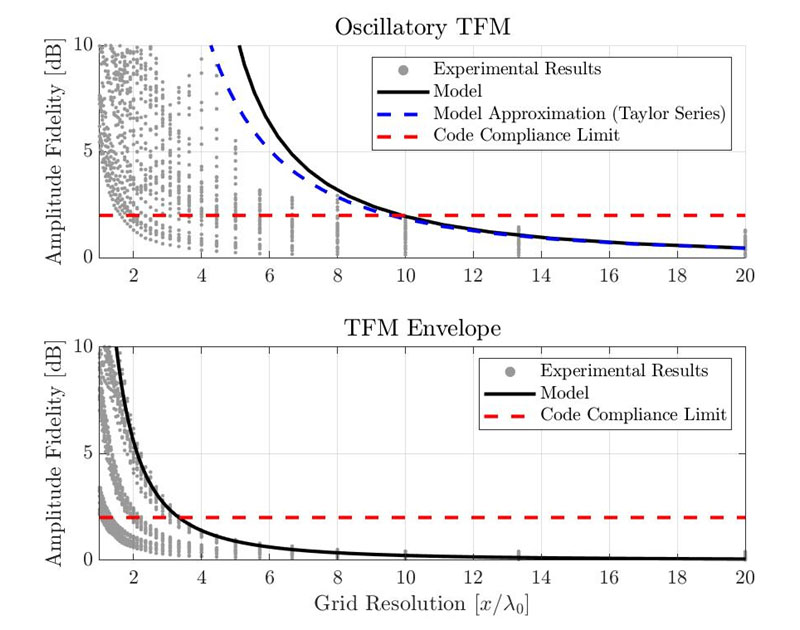
Figura 6. Comparação entre as medições empíricas de fidelidade da amplitude e dos resultados do modelo gaussiano proposto para o TFM oscilatório padrão (em cima) e para o envelope de TFM (embaixo).
Com o modelo proposto, a resolução necessária para estar em conformidade com o código é λ0/9,9 para o TFM oscilatório padrão e λ0/3,3 para o envelope de TFM. Os resultados experimentais demonstram que a resolução mínima da grade para estar em conformidade com o código é de cerca de λ0/10 para o TFM oscilatório padrão e de λ0/3,3 para o envelope de TFM. No entanto, observe que esses valores foram obtidos do pior caso experimental apresentado. Alguns dos valores de fidelidade da amplitude medidos são inferiores a 2 dB, mesmo com uma resolução de grade menos precisa. Portanto, o modelo proposto fornece estimativas boas, porém conservadoras, para a fidelidade da amplitude de uma configuração de TFM.
Conclusão
A fidelidade da amplitude de uma configuração de TFM é uma medida importante da robustez da formação de imagem em relação à resolução da grade. Quanto mais densa a grade, menor o valor de fidelidade da amplitude. Os códigos e normas agora incluem o método de foco total como uma nova técnica de inspeção e requerem que a fidelidade da amplitude seja de 2 dB ou menos. Este artigo apresenta como a fidelidade da amplitude pode ser medida corretamente de forma empírica e propõe um modelo analítico simples para estimar a fidelidade da amplitude dos resultados de uma configuração de TFM.
Um modelo analítico simples foi proposto com base no perfil da amplitude ao longo do eixo principal de propagação acústica. O modelo estima o perfil da amplitude como uma oscilação gaussiana modulada por cosseno. Usar este perfil para estimar a fidelidade da amplitude leva a bons resultados tanto para o TFM oscilatório padrão como para o envelope de TFM. Os resultados empíricos demonstraram a necessidade de uma resolução da grade de até λ0/10 ou λ0/3,3, respectivamente, para o TFM oscilatório padrão e para o envelope de TFM. O modelo analítico proposto estima a necessidade de uma resolução da grade de λ0/9,9 para o TFM padrão e de λ0/3,3 para o envelope de TFM. O modelo proposto pode, portanto, ser usado para estimar a fidelidade da amplitude da configuração de TFM.
Para saber mais sobre os benefícios do uso do envelope de TFM como parte de uma solução em conformidade com o código, leia o artigo “Uso do método de foco total com o recurso de envelope.”
Bibliografia
[1] ASME Committee, 2019, “ASME BPVC.V Article 4 Mandatory Appendix XI Full Matric Capture.”
[2] Oralkan, O., Ergun, A. S., Johnson, J. A., Karaman, M., Demirci, U., Kaviani, K., Lee, T. H., e Khuri-Yakub, B. T., 2002, “Capacitive Micromachined Ultrasonic Transducers: Next-Generation Arrays for Acoustic Imaging?,” IEEE Trans. Ultrason., Ferroelect., Freq. Contr., 49(11), pp. 1596–1610.
[3] Thomenius, K. E., 1996, “Evolution of Ultrasound Beamformers,” 1996 IEEE Ultrasonics Symposium. Proceedings, IEEE, San Antonio, TX, EUA, pp. 1615–1622.
[4] Freeman, S., Li, P., e O’Donnell, M., “Retrospective Dynamic Transmit Focusing,” p. 24.
[5] Wilcox, P. D., 2006, “Exploiting the Full Data Set from Ultrasonic Arrays by Post-Processing,” AIP Conference Proceedings, AIP, Brunswick, Maine (EUA), pp. 845–852.
[6] Portzgen, N., Gisolf, D., e Blacquiere, G., 2007, “Inverse Wave Field Extrapolation: A Different NDI Approach to Imaging Defects,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 54(1), pp. 118–127.
[7] Sharpe, R. S., ed., 1982, Research Techniques in Nondestructive Testing. Vol. 6: ..., Acad. Press, Londres.
[8] Holmes, C., Drinkwater, B. W., e Wilcox, P. D., 2008, “Advanced Post-Processing for Scanned Ultrasonic Arrays: Application to Defect Detection and Classification in Non-Destructive Evaluation,” Ultrasonics, 48(6–7), pp. 636–642.
[9] Holmes, C., Drinkwater, B. W., e Wilcox, P. D., 2005, “Post-Processing of the Full Matrix of Ultrasonic Transmit–Receive Array Data for Non-Destructive Evaluation,” NDT & E International, 38(8), pp. 701–711.
[10] ISO, 2020, “ISO/DIS 23865 -FMC-TFM - General Use of TFM-FMC Technique.”
[11] Johnson, P., 2019, “With a New Software Wizard, There’s No Sorcery but the Magic of the M2M Gekko Is Evident with Instant Code Compliance for Your TFM Weld Inspections.,” Code Compliant TFM Weld Inspection with Three Clicks.
[12] ASME Committee, 2019, “ASME BPVC.V Article 4 Nonmandatory Appendix F - Examination of Welds Using Full Matrix Capture.”