包络功能使全聚焦方式更出色

Аннотация

В настоящей работе вы узнаете, как рассчитать огибающую TFM-изображения, и каковы преимущества использования огибающей TFM. Огибающая TFM получается путем вычисления нормы двух разных TFM-изображений, где первое изображение TFM получено с помощью стандартного метода FMC (полноматричного захвата), а второе TFM-изображение — с помощью FMC и преобразования Гильберта. Полученное в результате изображение огибающей TFM является оптимальным для амплитудного метода измерения размеров дефектов, поскольку более устойчиво к колебаниям амплитуды по сравнению со стандартным TFM-изображением при идентичном разрешении сетки. Таким образом, по сравнению со стандартным TFM-изображением, для огибающей TFM можно использовать более грубое разрешение сетки, что сокращает общее количество вычислительных затрат и, в конечном итоге, увеличивает скорость сбора данных.

Введение

Метод общей фокусировки (TFM) относительно недавно начал применяться для неразрушающего контроля материалов и структур. Некоторые стандарты теперь включают раздел по методам FMC и TFM в рамках неразрушающего контроля (НК) [1], [2].

Некоторые устройства неразрушающего контроля, такие как дефектоскоп OmniScan™ X3, позволяют получать TFM-изображения в режиме реального времени. Подход TFM с использованием FMC резюмируется в следующем разделе, но основная предпосылка состоит в том, что TFM базируется на суммировании множества значений амплитуды элементарных A-сканов. TFM-изображения являются колебательными из-за происхождения акустических волн элементарных A-сканов. С другой стороны, схемы характеризации, найденные в приложениях неразрушающего контроля, по существу основаны на амплитудных методах, для которых колебательное поведение можно рассматривать как акустический артефакт. Обычной практикой для адаптации колебательного поведения к схемам характеризации, является выпрямление амплитуды с целью получения изображения со строго положительными значениями. Этот подход может облегчить интерпретацию изображения; но в данной статье мы покажем, как использовать огибающую сигнала, чтобы еще больше улучшить анализ и увеличить скорость сбора данных по сравнению со стандартным TFM-изображением.

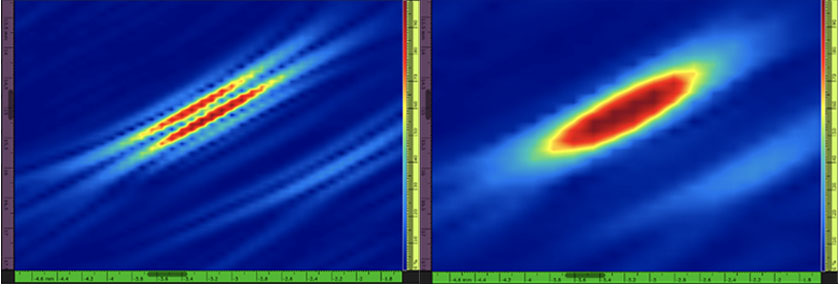
Рис. 1— Слева: Пример TFM-изображения бокового сверления (SDH) со строго положительными значениями амплитуды и колебанием сигнала (т.е. стандартное TFM-изображение). Разрешение сетки: 0,08 мм (λ/8,1) и макс. амплитуда: 108,7%. Справа: Огибающая TFM того же самого SDH. Разрешение сетки: 0,16 мм (λ/4) и макс. амплитуда: 122,6%.

Есть несколько недостатков использования такого колебательного TFM-изображения. Во-первых, разрешение сетки TFM, т.е. расстояние между двумя пикселями в кадре, должно быть приблизительно λ/8, в соответствии с требованиями стандарта [1]–[3]. В данной статье, λ — длина волны, обусловленная центральной частотой ПФР и скоростью звука в объекте. Малое разрешение сетки подразумевает большие вычислительные затраты, что приводит к снижению скорости сбора данных. На надежность методов измерения размеров дефектов на базе амплитуды также влияет колебательное TFM-изображение. Действительно, максимальная амплитуда измеренного эхо-сигнала сильно зависит от сдвига фазы полученного сигнала.

Все эти проблемы могут быть решены с помощью огибающей TFM, поскольку она устраняет колебания сигнала на изображении и позволяет более точно измерять максимальную амплитуду (см. Рис. 1). Производительность сбора данных выигрывает от использования огибающей TFM, поскольку требуется меньшее разрешение сетки, т.е. больший интервал между двумя соседними пикселями, для получения такой же амплитудной устойчивости по сравнению со стандартным TFM. Например, разрешение сетки приблизительно λ/4 достаточно для огибающей TFM, чтобы иметь ту же точность амплитуды (2 дБ), что стандартное TFM-изображение с разрешением λ/8 [3].

Цель данной работы — информировать специалиста по неразрушающему контролю о преимуществах использования огибающей TFM. Сначала мы вкратце опишем суть метода FMC-TFM, а затем изложим концепции вычисления и построения огибающей TFM. И наконец, мы представим преимущества использования огибающей TFM по сравнению со стандартным изображением TFM колебательного типа.

Краткое изложение подхода FMC-TFM

Отличительной чертой ультразвуковой фазированной решетки является способность фокусироваться в любой желаемой точке в объекте контроля. Тип фокусировки, используемой в технологии фазированных решеток, использует задержки как при передаче, так и при приеме, для синхронизации времени пролета коротких импульсных сигналов в интересуемых точках. В фокальной зоне объекта, общая ширина генерируемого акустического луча уменьшается, а соответствующее разрешение обнаружения существенно увеличивается [4]–[12].

Метод TFM — естественное расширение данной возможности; TFM генерирует сфокусированный луч путем фокусирования и управления лучом фазированной решетки в ​​каждом положении области интереса внутри объекта. На экране отображаются только точки с высокой разрешающей способностью [13]–[16]. Зачастую область интереса состоит из одной общей декартовой сетки для всех целевых фокальных точек. Очевидно, что для выполнения фокусировки в каждой позиции сетки с использованием физического формирования луча было бы чрезвычайно долго из-за времени распространения звука, необходимого для достижения каждой позиции.

Поскольку типичные ультразвуковые акустические волны в приложениях НК являются линейными, физическое формирование луча, возникающее в результате наложения акустических полей для всех составляющих элементов данной апертуры, может эмулироваться после сбора данных на базе полноматричного захвата (FMC). Извлечение набора данных FMC требует записи сигнала от всех элементов, составляющих принимающую апертуру, в то время как акустическая эмиссия создается каждым отдельным элементом, составляющим апертуру передачи. Как таковой, набор данных FMC формируется множеством элементарных A-сканов для всех комбинаций передающих и принимающих элементов.

Как и в случае сфокусированных фазированных решеток, для получения фокусированной амплитуды из заданного положения фокусировки требуется следующее:

• Вычисление времени пролета, необходимого для распространения звука, чтобы достичь фокального положения, соответствующего выбранной позиции сетки, и обратно к принимающему элементу, для всех пар элементов приема/передачи апертуры
• Выбор точки данных амплитуды, соответствующей времени пролета передачи-приема для всех пар передающих-приемных элементов апертуры
• Суммирование всех выбранных точек данных амплитуды по всем элементам приема-передачи апертуры
• Размещение результирующей суммарной амплитуды в первоначально выбранной позиции сетки

Повторение этих шагов для всех позиций сетки в области интереса создает карту амплитуд, для которой все значения амплитуды соответствуют сфокусированному лучу в режиме передаче и режиме приема. Этот способ использования данных FMC для создания карты амплитуды, сфокусированной в каждой позиции области интереса (то есть зоне TFM) называется подходом FMC-TFM.

Как вычисляется огибающая TFM

Данный раздел описывает, как вычислить огибающую TFM с помощью тех же элементарных A-сканов (FMC), которые были получены для стандартного TFM. Следует отметить, что огибающая имеет физическое проявление и не является простым алгоритмом сглаживания изображения. Огибающая TFM-изображения напрямую происходит из составляющих ее отдельных А-сканов. Чтобы это схематически проиллюстрировать, концепция огибающей представлена ​​с использованием временного ряда гауссова импульса. Процесс также применяется к эмпирическому A-скану и к полному кадру TFM.

Сигнал a(t) соответствует полученному сигналу, —т.е. эквиваленту элементарного A-скана, полученного с помощью FMC, — и фактически является частью сложного аналитического сигнала z(t), который можно записать как:

где a’(t) соответствует мнимой части аналитического сигнала, а θ(t) — мгновенная фаза сигнала. Мнимая часть эффективно вычисляется с использованием преобразования Гильберта [17]. Огибающая сигнала соответствует норме аналитического сигнала, которую можно записать как:

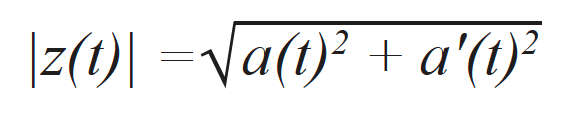
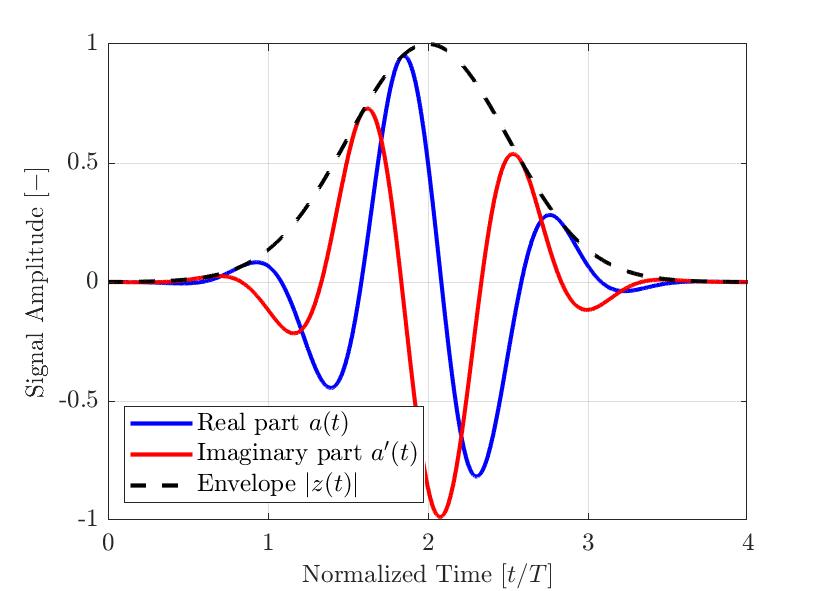
Рис. 2: Типичный модулированный гауссовский импульс для приложений НК. Показаны действительная и мнимая части, а также вычисленная огибающая. Временная ось нормализуется с выбранным периодом центральной частоты импульса.

На Рис. 2 показан пример простого модулированного гауссовского импульса a(t). Реальный сигнал a (t) выделен синим цветом; мнимая часть, преобразованная по Гильберту a ’(t), выделена красным; и результирующая огибающая |z(t)| — пунктирной линией. Как видно из уравнения выше, огибающая сигнала |z(t)| не зависит от мгновенной фазы θ(t) сигнала. Следовательно, сигналы с разными сдвигами фазы ϕ могут иметь одинаковую огибающую. Рис. 3 отображает несколько модулированных гауссовских импульсов с разными сдвигами фазы ϕ и результирующей огибающей. Следовательно, при использовании огибающей сигнала, измеренная максимальная амплитуда сигнала более устойчива, чем абсолютное значение реального компонента аналитического сигнала.

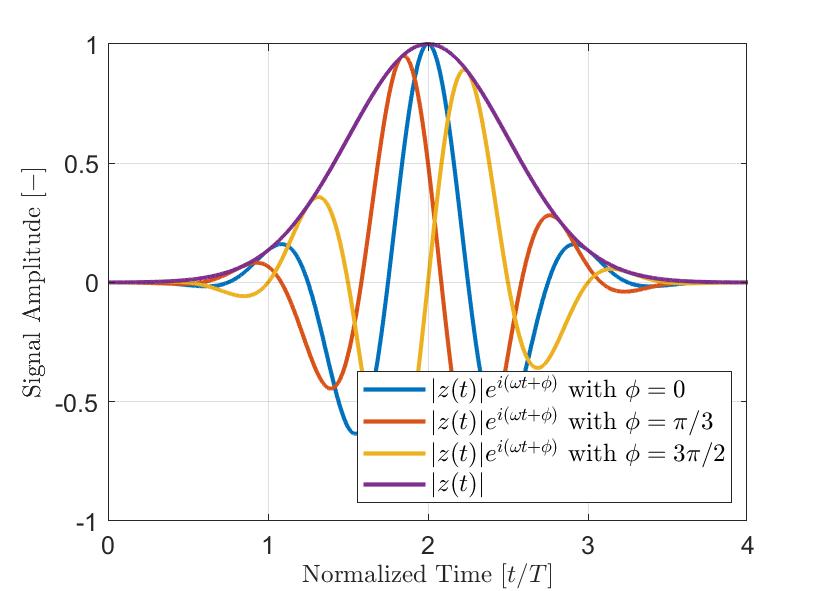
Рис. 3: Типичные модулированные гауссовские импульсы (|z(t)|e^i(ωt+ϕ)) с разными сдвигами фаз ϕ. Огибающая |z(t)| сигналов не зависит от мгновенной фазы аналитического сигнала.

Этот же процесс может быть использован для получения огибающей эмпирического А-скана. На Рис. 4 показан типичный элементарный A-скан, полученный с помощью FMC, а на Рис. 5 — тот же A-скан (синий) с преобразованием Гильберта (красный) и вычисленной огибающей (пунктирная линия). Все отображенные сигналы приведены к максимуму огибающей амплитуды.

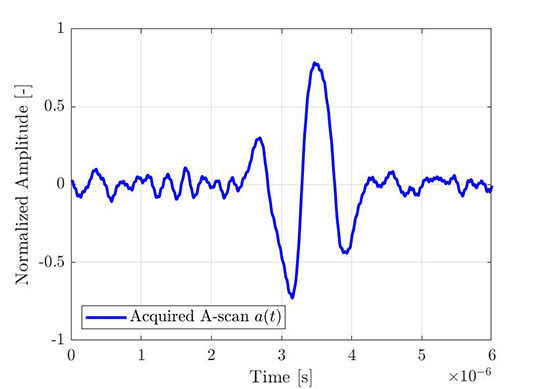Рис. 4: Часть полученного элементарного A-скана (из набора данных FMC).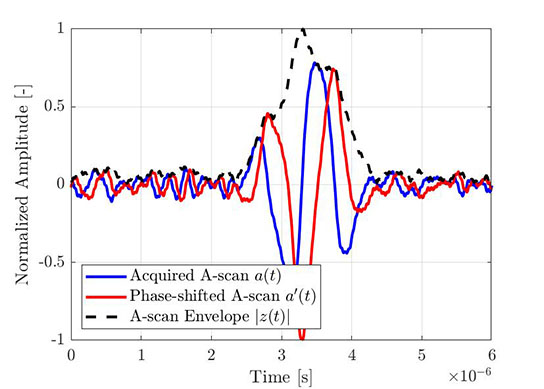

Рис. 5: Этот же элементарный А-скан с преобразованием Гильберта и вычисленной огибающей.

Изображение огибающей TFM, включая индексы точек сетки (k,l), рассчитывается с помощью аналитических сигналов от всех содействующих A-сканов [15]. Фактически, это результат расчета нормы аналитического TFM-изображения y(k,l), представляющего стандартный кадр TFM x(k,l), полученный с помощью набора данных FMC и кадра TFM x'(k,l), вычисленного путем преобразования Гильберта данных FMC. В обоих случаях, используются одни и те же задержки. Огибающая TFM затем рассчитывается с помощью следующего выражения:

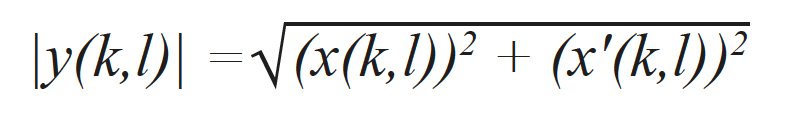
Таким образом, изображение огибающей TFM является результатом комбинации двух изображений TFM (см. Рис. 6): одно из реального компонента элементарных A-сканов, а другое — из найденного мнимого компонента элементарных A-сканов. Несмотря на то, что этот процесс усложняет процесс вычисления и снижает скорость сбора данных устройства НК, мы покажем в следующем разделе, что разрешение сетки можно существенно уменьшить, не влияя на точность амплитуды, одновременно увеличивая скорость сбора данных до более высокого уровня, чем при стандартном TFM.

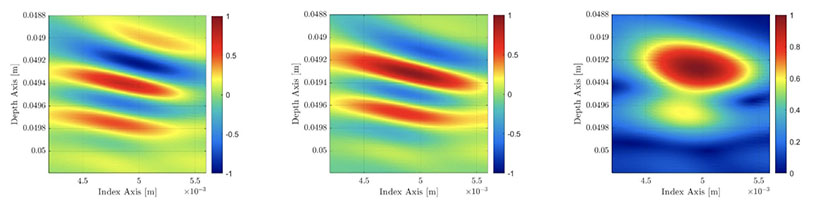
Рис. 6 (слева): кадр стандартного TFM (не в абсолютном значении). В центре: кадр TFM, вычисленный с использованием преобразования Гильберта FMC. Справа: результирующее изображение огибающей TFM.

Преимущества использования огибающей TFM

В этом разделе, мы демонстрируем преимущества огибающей TFM, сравнивая TFM-кадры с разными коэффициентами разрешения сетки (от λ/9,3 до λ/4,0) и отслеживая критические показатели контроля. Результаты получены с помощью преобразователя 5L32-A31 и призмы SA31-N55S-IHC на стальном образце с боковым отверстием (SDH) диам. 1 мм (см. Рис. 7). Между призмой и стальным образцом использовалась контактная жидкость (Sonotech Ultragel II) . Данные получены с использованием дефектоскопа OmniScan™ X3 (Olympus). Выбран режим распространения импульс-эхо (T-T), размер зоны составляет 20 мм × 20 мм. Длина волны, связанная с выбранным объектом и акустическим путем, составляет λ = 0,648 мм. Разрешение сетки составляет долю длины волны.

Рис. 7: Снимок настройки, используемой для получения TFM-изображений из Табл. 1 Синий прямоугольник соответствует всей области интереса (20 мм × 20 мм), а красный прямоугольник — увеличенной зоне интереса (5 мм × 5 мм), показанной на изображениях в Табл. 1. Мы использовали преобразователь 5L32-A31 и призму SA31-N55S-IHC. Стальной образец имеет толщину 40 мм.

В Табл. 1 приведены результирующие изображения TFM для четырех разных значений разрешения сетки в диапазоне от λ/9,3 до λ/4,0, как для стандартного TFM, так и для огибающей TFM. Найденное значение точности амплитуды [3] и результирующая скорость сбора данных указаны на каждом изображении TFM.

Разрешение сетки	Стандартное TFM-изображение	Огибающая TFM
λ/9,3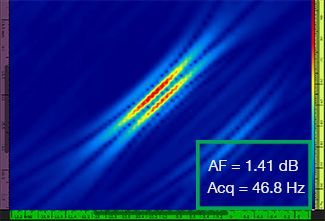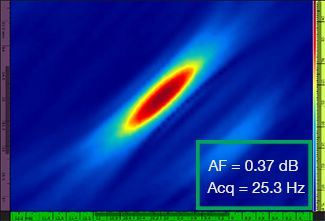
λ/8,1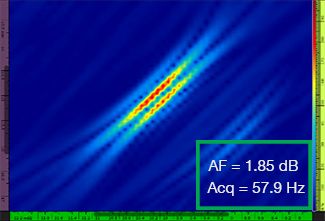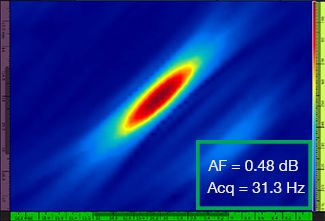
λ/5,9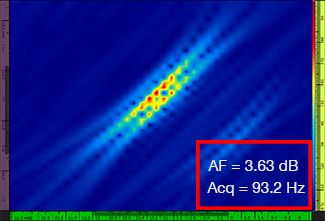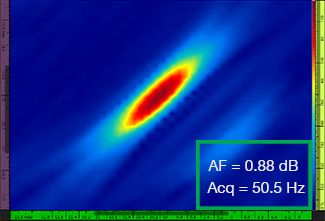
λ/4,0

Новые стандарты [1, 2] требуют, чтобы значение точности амплитуды составляло 2 дБ или меньше. Следовательно, только первые два значения разрешения сетки (λ/9,3; λ/8,1) соответствуют требованиям стандарта при использовании стандартного TFM. Огибающая TFM обеспечивает более грубое разрешение сетки (λ/4,0), сохраняя при этом точность амплитуды в соответствии с требованиями стандарта. В свою очередь, использование огибающей TFM с более грубой сеткой позволяет увеличить скорость сбора данных приблизительно на 37% по сравнению с самой высокой частотой сбора данных, достигаемой с помощью стандартного TFM (57,9 Гц при λ/8,1).

Заключение

Метод вычисления огибающей изображения TFM был представлен и проиллюстрирован на простых примерах. Мы показали, что огибающая сигнала не зависит от его мгновенной фазы и, следовательно, обеспечивает более надежную базу для методов определения размеров по амплитуде (таких как метод падения на 6 дБ). Огибающая сигнала — это не просто сглаживание изображения и не должна рассматриваться как фильтр, который может привести к потере данных. Преимущества использования огибающей в визуализации TFM были продемонстрированы путем сравнения изображений TFM с огибающей и без нее при разных значениях разрешения сетки. Даже если необходимо вычислить два изображения TFM для получения результирующей огибающей TFM, обработка может быть значительно упрощена за счет использования более грубого разрешения сетки, в соответствии с требованиями стандартов. Это связано с устойчивостью огибающей вне зависимости от колебаний амплитуды. В результате, мы получаем изображение, которое более приспособлено для определения размера амплитуды, но получено более быстрыми темпами, чем эквивалентное изображение, обработанное с помощью стандартного TFM.

Справочная литература

[1] ASME Committee, “ASME BPVC.V Article 4 Mandatory Appendix XI Full Matric Capture.” ASME, 2019.

[2] ASME Committee, “ASME BPVC.V Article 4 Nonmandatory Appendix F - Examination of Welds Using Full Matric Capture.” ASME, 2019.

[3] N. Badeau, A. Le Duff, and C.-H. Kwan, “Theoretical Model for Amplitude Fidelity Reading (submitted),” presented at the ASNT Research Symposium, 2020.

[4] A. C. Clay, S.-C. Wooh, L. Azar, and J.-Y. Wang, “Experimental Study of Phased Array Beam Steering Characteristics,” Journal of Nondestructive Evaluation, vol. 18, no. 2, p. 13, 1999.

[5] L. J. Bond, “Fundamentals of Ultrasonic Inspection,” ASM Handbook, vol. 17, no. Nondestructive Evaluation of Material, pp. 155–168, 2018.

[6] S.-J. Song, H. J. Shin, and Y. H. Jang, “Development of an ultra sonic phased array system for nondestructive tests of nuclear power plant components,” Nuclear Engineering and Design, vol. 214, no. 1–2, pp. 151–161, May 2002, doi: 10.1016/S0029-5493(02)00024-9.

[7] S. Mahaut, O. Roy, C. Beroni, and B. Rotter, “Development of phased array techniques to improve characterization of defect located in a component of complex geometry,” Ultrasonics, vol. 40, no. 1–8, pp. 165–169, May 2002, doi: 10.1016/S0041-624X(02)00131-2.

[8] S. C. Mondal, P. D. Wilcox, and B. W. Drinkwater, “Design of Two-Dimensional Ultrasonic Phased Array Transducers,” Journal of Pressure Vessel Technology, vol. 127, no. 3, pp. 336–344, Aug. 2005, doi: 10.1115/1.1991873.

[9] S.-C. Wooh and Y. Shi, “Influence of phased array element size on beam steering behavior,” Ultrasonics, vol. 36, no. 6, pp. 737–749, Apr. 1998, doi: 10.1016/S0041-624X(97)00164-9.

[10] Joon-Hyun Lee and Sang-Woo Choi, “A parametric study of ultrasonic beam profiles for a linear phased array transducer,” IEEE Trans. Ultrason., Ferroelect., Freq. Contr., vol. 47, no. 3, pp. 644–650, May 2000, doi: 10.1109/58.842052.

[11] R. Ahmad, T. Kundu, and D. Placko, “Modeling of phased array transducers,” The Journal of the Acoustical Society of America, vol. 117, no. 4, pp. 1762–1776, Apr. 2005, doi: 10.1121/1.1835506.

[12] B. W. Drinkwater and P. D. Wilcox, “Ultrasonic arrays for non-destructive evaluation: A review,” NDT & E International, vol. 39, no. 7, pp. 525–541, Oct. 2006, doi: 10.1016/j.ndteint.2006.03.006.

[13] P. D. Wilcox, “Exploiting the Full Data Set from Ultrasonic Arrays by Post-Processing,” in AIP Conference Proceedings, Brunswick, Maine (USA), 2006, vol. 820, pp. 845–852, doi: 10.1063/1.2184614.

[14] J. Zhang, B. W. Drinkwater, and P. D. Wilcox, “Effects of array transducer inconsistencies on total focusing method imaging performance,” NDT & E International, vol. 44, no. 4, pp. 361–368, Jul. 2011, doi: 10.1016/j.ndteint.2011.03.001.

[15] C. Holmes, B. W. Drinkwater, and P. D. Wilcox, “Advanced post-processing for scanned ultrasonic arrays: Application to defect detection and classification in non-destructive evaluation,” Ultrasonics, vol. 48, no. 6–7, pp. 636–642, Nov. 2008, doi: 10.1016/j.ultras.2008.07.019.

[16] C. Holmes, B. W. Drinkwater, and P. D. Wilcox, “Post-processing of the full matrix of ultrasonic transmit–receive array data for non-destructive evaluation,” NDT & E International, vol. 38, no. 8, pp. 701–711, Dec. 2005, doi: 10.1016/j.ndteint.2005.04.002.

[17] D. Gabor, “Theory of Communication,” Journal of the Institution of Electrical Engineers, vol. 96, pp. 429–441, 1946.