包络功能使全聚焦方式更出色

Résumé

Cet article explique comment effectuer le traitement de l’enveloppe d’une image obtenue au moyen de la méthode TFM (total focusing method) et les avantages d’utiliser ce calcul d’enveloppe dans le cadre d’une solution d’inspection qui doit respecter la conformité aux normes. Le traitement de l’enveloppe TFM s’effectue en calculant la norme de deux images TFM différentes, à savoir une première image acquise au moyen de la méthode FMC (full matrix capture) standard, et une seconde image acquise au moyen de la méthode FMC à laquelle on a appliqué la transformée de Hilbert. Il en résulte une image d’enveloppe TFM mieux adaptée à la méthode de mesure fondée sur l’amplitude puisque pour une résolution de grille identique, elle offre une meilleure résistance à la variation d’amplitude qu’une image TFM oscillatoire standard. Par conséquent, en comparaison avec une image TFM oscillatoire standard, il faut utiliser une résolution de grille plus grossière pour le traitement de l’enveloppe afin de réduire l’importance du calcul total et, ultimement, accroître le taux d’acquisition.

Introduction

La méthode TFM est une technique d’inspection récemment acceptée dans l’industrie pour le contrôle non destructif (CND) des matériaux et des structures. Ainsi, certains codes et normes comprennent désormais une section portant sur la méthode d’inspection FMC et la technique d’acquisition TFM dans le cadre d’applications de CND (voir [1] et [2]).

Certains appareils de recherche de défauts, comme l’OmniScan™ X3 d’Olympus, permettent l’acquisition d’une image TFM en temps réel. L’approche TFM tirant profit de la technique d’acquisition FMC est résumée dans la section suivante; fondamentalement, la méthode TFM exécute la somme d’une multitude de valeurs d’amplitude provenant de A-scans élémentaires. Les images TFM oscillent en raison de l’origine des ondes acoustiques provenant des A-scans élémentaires. Par ailleurs, les schémas de caractérisation trouvés dans les applications de CND proviennent essentiellement de techniques basées sur l’amplitude pour lesquelles le phénomène oscillatoire peut être considéré comme un artefact acoustique superflu. Une pratique courante utilisée pour adapter l’oscillation aux schémas de caractérisation consiste à corriger l’amplitude, de sorte que l’image n’affiche que des valeurs strictement positives. Cette approche facilite certainement l’interprétation de l’image par rapport à son équivalent entièrement oscillant; toutefois, cet article montrera comment le traitement de l’enveloppe du signal peut améliorer davantage la caractérisation et accroître réellement le taux d’acquisition par rapport à une image TFM oscillatoire standard.

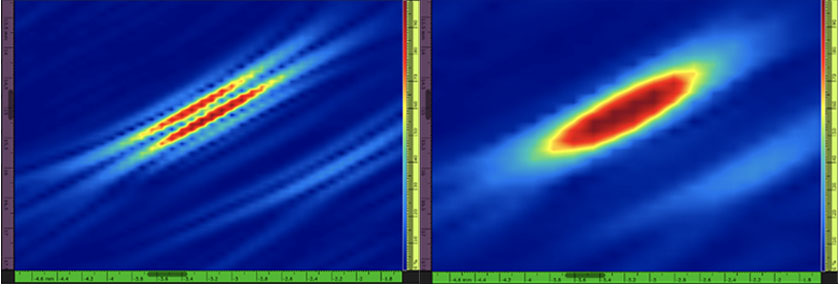
Figure 1 — À gauche : Exemple d’une image TFM provenant d’un trou génératrice (SDH) affichant des valeurs d’amplitude strictement positives et une oscillation du signal (c’est-à-dire, image TFM standard). La résolution de la grille est de 0,08 mm (λ/8,1) et l’amplitude maximale est de 108,7 %. À droite : Image obtenue après le traitement d’enveloppe TFM pour le même trou génératrice (SDH). La résolution de la grille est de 0,16 mm (λ/4,0) et l’amplitude maximale est de 122,6 %.

Il y a plusieurs inconvénients à utiliser une image TFM oscillante de ce type. D’abord, la résolution de la grille TFM, soit la distance entre deux pixels dans la trame de l’image, doit être d’environ λ/8 pour respecter la norme (voir [1] et [3]). Dans cet article, la valeur λ correspond à la longueur d’onde associée à la fréquence centrale de la sonde et à la vitesse de propagation dans la pièce. Le calcul important que suppose une résolution de grille réduite fait immédiatement diminuer le taux d’acquisition. La fiabilité des méthodes de dimensionnement des défauts basées sur l’amplitude est également influencée par l’image TFM oscillatoire. En effet, l’amplitude maximale d’un écho mesuré dépend fortement du décalage de phase du signal acquis.

On peut remédier à tous ces inconvénients grâce au traitement d’enveloppe TFM, car il supprime les oscillations du signal dans l’image et assure une meilleure fiabilité de la mesure d’amplitude maximale (figure 1). Le traitement d’enveloppe TFM augmente l’efficacité de l’acquisition puisqu’il requiert une résolution de grille réduite — soit l’application d’un espacement plus important entre deux pixels adjacents — pour l’obtention de la même robustesse d’amplitude par rapport à une image TFM standard. Par exemple, pour le traitement d’enveloppe TFM, l’application d’une résolution de grille d’environ λ/4 est suffisante pour obtenir la même fidélité d’amplitude (2 dB) que celle d’une image TFM oscillatoire standard à laquelle on a appliqué une résolution de λ/8 (voir [3]).

L’objectif de ce document est d’informer le spécialiste du CND des avantages de l’utilisation du traitement d’enveloppe TFM. Nous présentons d’abord un résumé de l’approche FMC/TFM, suivi d’une brève présentation des concepts entourant le calcul de l’enveloppe TFM. Ensuite, nous présentons les avantages du traitement de l’enveloppe TFM dans le cadre d’une solution d’inspection conforme au code par rapport à l’utilisation d’images TFM oscillatoires standard.

Résumé de l’approche FMC/TFM

La caractéristique principale de la technologie d’inspection par ultrasons multiéléments est sa capacité de focalisation à n’importe quelle position souhaitée dans une pièce inspectée. Le type de focalisation qu’applique cette technologie utilise des délais tant en émission qu’en réception pour synchroniser le temps de vol des signaux courts émis à la zone d’intérêt. Au point de focalisation dans la pièce inspectée, la largeur globale du faisceau sonore généré se rétrécit et la résolution de détection correspondante augmente considérablement (voir [4] et [12]).

La méthode TFM constitue une extension naturelle de cette capacité; elle produit un faisceau focalisé par la focalisation et la déflexion des ultrasons multiéléments sur chaque position de la région d’intérêt à l’intérieur de la pièce inspectée. Seul l’ensemble des points de données focalisés à très haute résolution s’affiche à l’écran (voir [13] et [16]). Souvent, la région d’intérêt consiste en une grille cartésienne uniforme intégrant toutes les cibles de focalisation requises. De toute évidence, l’exécution de cette focalisation à chaque position de la grille en appliquant une formation de faisceau physique classique se révélerait excessivement longue en raison du temps de propagation acoustique physique requis pour atteindre chaque position d’intérêt.

Comme les ondes ultrasonores typiques des applications de CND sont linéaires, la formation du faisceau physique résultant de la superposition de champs acoustiques réels pour tous les éléments d’une ouverture donnée peut être reproduite au cours d’un processus post-acquisition basé sur l’ensemble des données d’acquisition FMC. La récupération de l’ensemble de données FMC nécessite d’enregistrer le signal de tous les éléments de l’ouverture de réception tandis qu’une émission acoustique est produite par chaque élément individuel de l’ouverture de transmission. Ainsi, l’ensemble de données FMC réunit la multitude de A-scans élémentaires de toutes les combinaisons d’éléments d’émission et de réception.

Comme pour les ultrasons multiéléments focalisés, l’obtention de l’amplitude focalisée à partir d’une position donnée nécessite les éléments suivants :

• Le calcul du temps de vol nécessaire à la propagation sonore pour atteindre la position focale correspondant à une position d’intérêt sélectionnée dans la grille et pour son retour vers l’élément récepteur, pour toutes les paires d’éléments d’émission et de réception de l’ouverture.
• La sélection du point de données d’amplitude correspondant au temps de vol d’émission-réception complet approprié pour toutes les paires d’éléments d’émission et de réception de l’ouverture.
• La somme de tous les points de données d’amplitude sélectionnés pour tous les éléments d’émission et de réception de l’ouverture
• Le positionnement de l’amplitude sommée obtenue à la position initialement sélectionnée dans la grille.

La répétition de ces étapes pour toutes les positions de la grille sur la région d’intérêt produit une carte d’amplitude pour laquelle toutes les valeurs correspondent à un faisceau focalisé, tant en émission qu’en réception. Cette méthode qui consiste à utiliser les données FMC pour produire une carte d’amplitude focalisée sur chaque point de la région d’intérêt (soit, la zone TFM) s’appelle « approche FMC/TFM ».

Méthode de calcul de l’enveloppe TFM

Cette section décrit comment l’enveloppe TFM est calculée à partir des mêmes A-scans élémentaires (données FMC) que ceux acquis par la méthode TFM standard. Notons que l’enveloppe existe physiquement et qu’il ne s’agit pas du résultat d’un simple algorithme de lissage d’image. L’enveloppe de l’image TFM provient directement des A-scans individuels la constituant. Tout d’abord, pour illustrer son comportement de façon schématique, le concept d’enveloppe est présenté à l’aide d’une série temporelle d’impulsions gaussiennes. Le processus est également appliqué à un A-scan empirique et à une trame d’image TFM entière.

Le signal a (t) correspond au signal acquis, soit l’équivalent d’un A-scan élémentaire acquis par acquisition FMC, et il constitue en fait la partie réelle d’un signal analytique complexe z (t), qui peut s’exprimer comme suit :

où a’(t) correspond à la partie imaginaire du signal analytique, et θ(t) correspond à la phase instantanée du signal. Le calcul réel de la partie imaginaire du signal s’effectue au moyen de la transformée de Hilbert (voir [17]). L’enveloppe du signal correspond à la norme du signal analytique, qui peut s’exprimer comme suit :

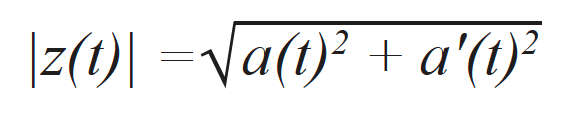
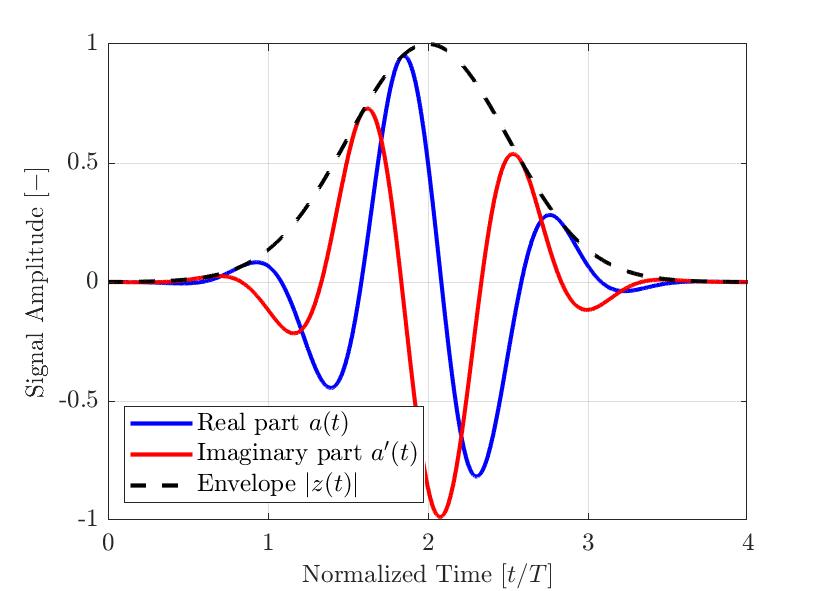
Figure 2 — Impulsion gaussienne modulée typique pour les applications de CND. Les parties réelles et imaginaires, ainsi que l’enveloppe calculée, sont illustrées. L’axe du temps est normalisé selon la période de fréquence centrale sélectionnée de l’impulsion.

La Figure 2 illustre un exemple d’impulsion gaussienne modulée simple a(t). Le signal réel a(t) apparaît en bleu, sa partie imaginaire a’(t) à laquelle la transformée de Hilbert a été appliquée apparaît en rouge, et l’enveloppe résultante |z(t)| est représentée par la ligne pointillée. Comme le montre l’équation ci-dessus, l’enveloppe du signal |z(t)| n’est pas influencée par la phase instantanée θ(t) du signal. Donc, les signaux présentant différents décalages de phase ϕ possèdent la même enveloppe. La figure 3 montre plusieurs impulsions gaussiennes modulées présentant différents décalages de phase ϕ et l’enveloppe qui en résulte. Par conséquent, lorsqu’on utilise l’enveloppe du signal, l’amplitude maximale mesurée est plus robuste que la valeur absolue de la composante réelle du signal analytique.

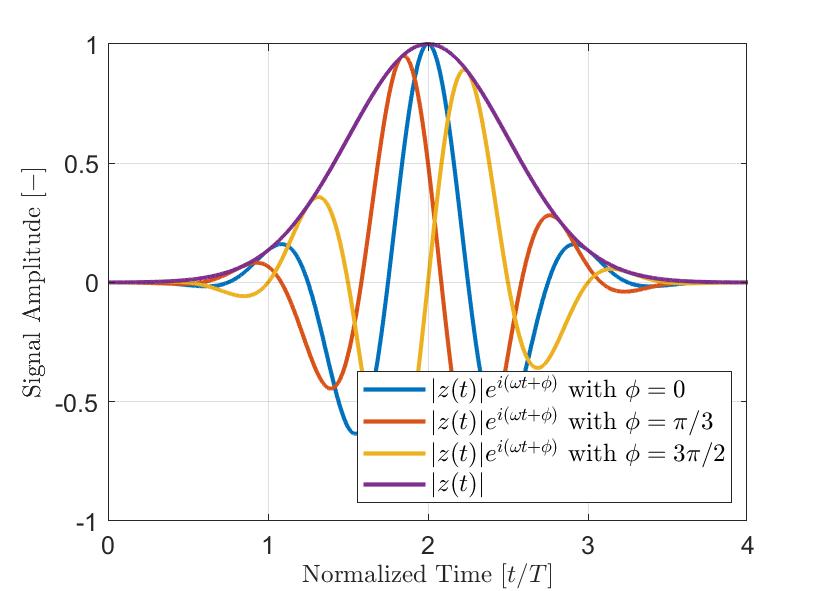
Figure 3 — Impulsions gaussiennes modulées typiques (|z(t)|e^i(ωt+ϕ)) présentant différents décalages de phase ϕ. L’enveloppe |z(t)| des signaux est nettement indépendante de la phase instantanée du signal analytique.

Le même processus peut être utilisé pour obtenir l’enveloppe d’un A-scan empirique. La figure 4 montre un A-scan élémentaire typique acquis à partir d’une acquisition FMC, tandis que la figure 5 montre le même A-scan (bleu) auquel on a appliqué la transformée de Hilbert (rouge) et l’enveloppe qui en résulte (ligne pointillée). Tous les signaux affichés sont normalisés au maximum de l’enveloppe d’amplitude.

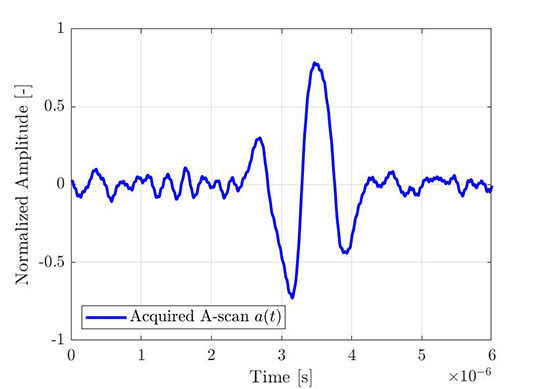Figure 4 — Portion d’un A-scan élémentaire acquis (à partir d’une acquisition FMC).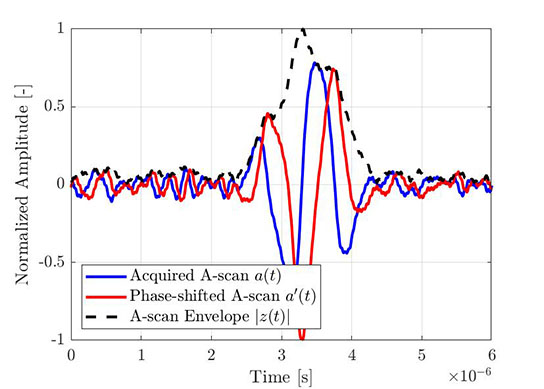

Figure 5 — Le même A-scan auquel on a appliqué la transformée de Hilbert, et l’enveloppe qui en résulte.

L’image d’enveloppe TFM — y compris les index individuels de points de grille (k, l) — est calculée en utilisant les signaux analytiques provenant de tous ses A-scans connexes (voir [15]). Il s’agit, en fait, du résultat du calcul de la norme d’une image TFM analytique y(k,l) composée de la trame de l’image TFM standard x(k,l) calculée à partir des données d’acquisition FMC standard et d’une trame d’image TFM x'(k,l) calculée à partir de la transformée de Hilbert des données FMC. Dans les deux cas, on utilise les mêmes groupes de délais. L’enveloppe TFM est ensuite calculée à l’aide de l’expression suivante

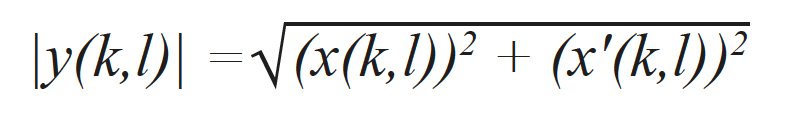
Une image d’enveloppe TFM est donc le résultat de la combinaison de deux images TFM (voir figure 6) : l’une issue de la composante réelle des A-scans élémentaires, et l’autre issue de la composante imaginaire calculée à partir de tous les A-scans élémentaires. Bien que ce processus augmente la complexité du calcul et réduit la vitesse d’acquisition de l’appareil de CND, nous démontrons dans la section suivante que la résolution de grille requise peut être réduite de manière considérable sans influencer la fidélité d’amplitude, tout en augmentant la vitesse d’acquisition à un taux plus élevé qu’avec la méthode TFM standard.

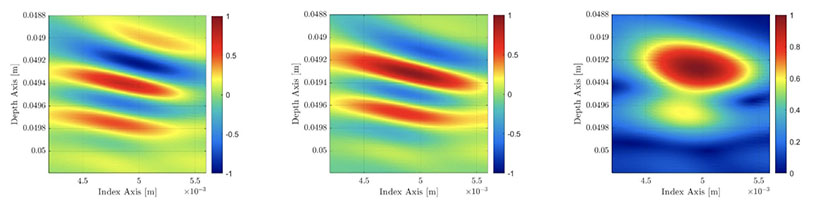
Figure 6 — Gauche : trame d’image TFM standard (sans valeur absolue). Centre : trame d’image TFM calculée à l’aide de la transformée de Hilbert de l’acquisition FMC. Droite : image de l’enveloppe TFM obtenue.

Avantages de l’utilisation de l’enveloppe TFM

Dans cette section, nous démontrons les avantages d’utiliser l’enveloppe TFM en comparant plusieurs trames d’image TFM auxquelles on a appliqué différents rapports de résolution de grille, allant de λ/9,3 à λ/4,0, et en surveillant diverses mesures d’inspection critiques. Ces résultats ont été obtenus à l’aide d’une sonde 5L32-A31 et d’un sabot SA31-N55S-IHC appliqués sur un bloc d’acier présentant un trou génératrice (SDH) de 1 mm de diamètre (voir figure 7). On a appliqué un gel de couplage (Sonotech Ultragel II) entre le sabot et le bloc d’acier. L’acquisition de données a été effectuée au moyen d’un appareil de recherche de défauts OmniScan™ X3 d’Olympus. On a choisi un mode de propagation par réflexion (T-T) est sélectionné, et la taille de la zone est de 20 mm × 20 mm. La longueur d’onde associée à la pièce et au mode de propagation sélectionnés est λ = 0,648 mm. La résolution de la grille est exprimée en fraction de longueur d’onde.

Figure 7 — Photo de la configuration utilisée pour acquérir les images TFM du tableau 1. Le rectangle bleu correspond à toute la région d’intérêt (20 mm × 20 mm), tandis que le rectangle rouge correspond à la région d’intérêt zoomée (5 mm × 5 mm) montrée dans les images du tableau 1. Nous avons utilisé une sonde 5L32-A31 et un sabot SA31-N55S-IHC. Le bloc d’acier a une épaisseur de 40 mm.

Le tableau 1 montre les images obtenues pour quatre valeurs de résolution de grille différentes, allant de λ/9,3 à λ/4,0, avec la méthode TFM standard et avec le traitement d’enveloppe TFM. La valeur de fidélité d’amplitude calculée (voir [3]) et le taux d’acquisition obtenu sont indiqués sur chacune des images TFM.

Résolution de la grille	Méthode TFM standard	Traitement d’enveloppe TFM
λ/9,3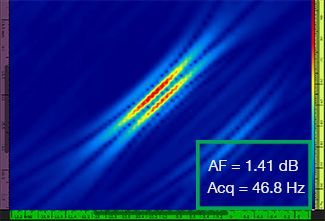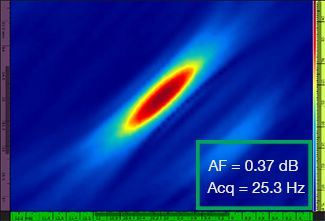
λ/8,1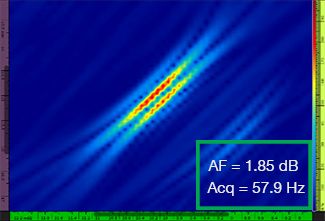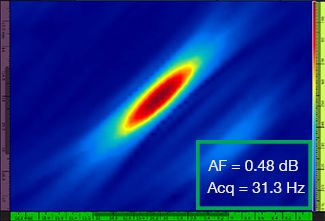
λ/5,9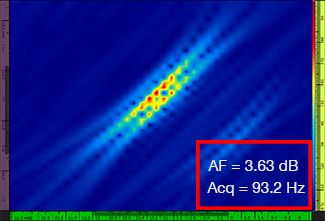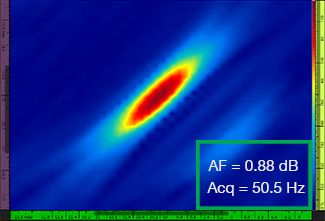
λ/4,0

Les codes et les normes nouvellement établis (voir [1, 2]) exigent que la valeur de fidélité d’amplitude soit de 2 dB ou moins. Donc, seules les deux premières valeurs de résolution de grille (λ / 9,3 et λ/8,1) permettent d’assurer la conformité au code lorsqu’on utilise la méthode TFM standard. L’enveloppe TFM permet une résolution de grille plus grossière (λ/4,0), tout en conservant une fidélité d’amplitude conforme au code. En retour, l’utilisation de l’enveloppe TFM avec une grille plus grossière entraîne une augmentation de la vitesse d’acquisition d’environ 37 % par rapport au taux d’acquisition le plus élevé atteint avec la méthode TFM standard conforme au code (57,9 Hz à λ/8,1).

Conclusions

La méthode de calcul de l’enveloppe d’une image TFM a été présentée et illustrée à l’aide d’exemples simples. Nous avons démontré que l’enveloppe d’un signal est indépendante de sa phase instantanée et, par conséquent, qu’elle fournit une base plus robuste pour les techniques de dimensionnement fondées sur l’amplitude (comme la méthode de chute de 6 dB). L’enveloppe du signal ne constitue pas un simple lissage d’image et ne doit pas être considérée comme un filtre, auquel cas une perte de données serait perçue. Les avantages de l’utilisation de l’enveloppe dans l’imagerie TFM ont été démontrés par des comparaisons d’images TFM, avec et sans l’enveloppe, pour différentes valeurs de résolution de la grille. Bien que deux images TFM doivent être calculées pour obtenir l’enveloppe TFM, le fardeau du traitement peut être considérablement réduit en utilisant une résolution de grille plus grossière, laquelle permet tout de même d’assurer la conformité au code. Cela est dû à la robustesse de l’enveloppe malgré la variation d’amplitude. Il en résulte une image mieux adaptée au dimensionnement d’amplitude, mais obtenue à un rythme plus rapide que l’image équivalente traitée par la méthode TFM standard.

Références

[1] Comité de l'American Society of Mechanical Engineers (ASME) « ASME BPVC.V Article 4 Mandatory Appendix XI Full Matric Capture » ASME, 2019.

[2] Comité de l'American Society of Mechanical Engineers (ASME) « ASME BPVC.V Article 4 Nonmandatory Appendix F - Examination of Welds Using Full Matric Capture » ASME, 2019.

[3] BADEAU N., LE DUFF A. et KWAN C.-H., « Theoretical Model for Amplitude Fidelity Reading (soumis) » présenté à l'occasion du symposium de recherche de l’ASNT, 2020.

[4] CLAY A. C., WOOH S.-C., AZAR L. et WANG J.-Y. « Experimental Study of Phased Array Beam Steering Characteristics », Journal of Nondestructive Evaluation, vol. 18, n° 2, p. 13, 1999.

[5] BOND L. J. « Fundamentals of Ultrasonic Inspection » ASM Handbook, vol. 17 : Nondestructive Evaluation of Material, pp. 155–168, 2018.

[6] SONG S.-J., SHIN H. J. et JANG Y. H. « Development of an ultra sonic phased array system for nondestructive tests of nuclear power plant components », Nuclear Engineering and Design, vol. 214, n° 1–2, pp. 151–161, mai 2002, système DOI : 10.1016/S0029-5493(02)00024-9.

[7] MAHAUT S., ROY O., BERONI C. et ROTTER B. « Development of phased array techniques to improve characterization of defect located in a component of complex geometry », Ultrasonics, vol. 40, n° 1–8, pp. 165–169, mai 2002, système DOI : 10.1016/S0041-624X(02)00131-2.

[8] MONDAL S. C., WILCOX P. D. et DRINKWATER B. W. « Design of Two-Dimensional Ultrasonic Phased Array Transducers », Journal of Pressure Vessel Technology, vol. 127, n° 3, pp. 336–344, août 2005, système DOI : 10.1115/1.1991873.

[9] WOOH S.-C. et SHI Y. « Influence of phased array element size on beam steering behavior », Ultrasonics, vol. 36, n° 6, pp. 737–749, avril 1998, système DOI : 10.1016/S0041-624X(97)00164-9.

[10] LEE Joon-Hyun et CHOI Sang-Woo « A parametric study of ultrasonic beam profiles for a linear phased array transducer », IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 47, n° 3, pp. 644–650, mai 2000, système DOI : 10.1109/58.842052.

[11] AHMAD R., KUNDU T. et PLACKO D. « Modeling of phased array transducers », The Journal of the Acoustical Society of America, vol. 117, n° 4, pp. 1762–1776, avril 2005, système DOI : 10.1121/1.1835506.

[12] DRINKWATER B. W. et WILCOX P. D. « Ultrasonic arrays for non-destructive evaluation: A review », NDT & E International, vol. 39, n° 7, pp. 525–541, octobre 2006, système DOI : 10.1016/j.ndteint.2006.03.006.

[13] WILCOX P. D. « Exploiting the Full Data Set from Ultrasonic Arrays by Post-Processing », AIP Conference Proceedings, Brunswick, Maine (É.-U.), 2006, vol. 820, pp. 845–852, système DOI : 10.1063/1.2184614.

[14] ZHANG J., DRINKWATER B. W. et WILCOX P. D. « Effects of array transducer inconsistencies on total focusing method imaging performance » NDT & E International, vol. 44, n° 4, pp. 361–368, juillet 2011, système DOI : 10.1016/j.ndteint.2011.03.001.

[15] HOLMES C., DRINKWATER B. W. Drinkwater et WILCOX P. D. « Advanced post-processing for scanned ultrasonic arrays: Application to defect detection and classification in non-destructive evaluation » Ultrasonics, vol. 48, n° 6–7, pp. 636–642, novembre 2008, système DOI : 10.1016/j.ultras.2008.07.019.

[16] HOLMES C., DRINKWATER B. W.et WILCOX P. D. « Post-processing of the full matrix of ultrasonic transmit–receive array data for non-destructive evaluation » NDT & E International, vol. 38, n° 8, pp. 701–711, décembre 2005, système DOI : 10.1016/j.ndteint.2005.04.002.

[17] GABOR D. « Theory of Communication » Journal of the Institution of Electrical Engineers, vol. 96, pp. 429–441, 1946.