概述
粗さパラメーターの選び方
|
| 凹凸の大きさを評価したい(Sq、Sa、Sz、Sp、Sv) | 高さの分布を評価したい(Ssk、Sku、ヒストグラム) |
| 目の細かさを評価したい(Sal、Sdq、Sdr) | 方向性を評価したい(Std、Str、方向プロット) |
| 周期性を評価したい(PSD) | 支配的な形状成分を評価したい(PSD) |
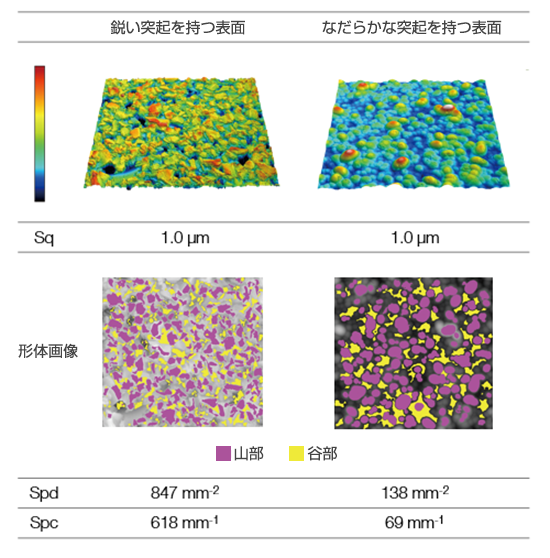
| 突起の数やその先端形状を評価したい(Spd、Spc) | 摩耗前後の変化量を評価したい(Sk、Spk、Svk) |
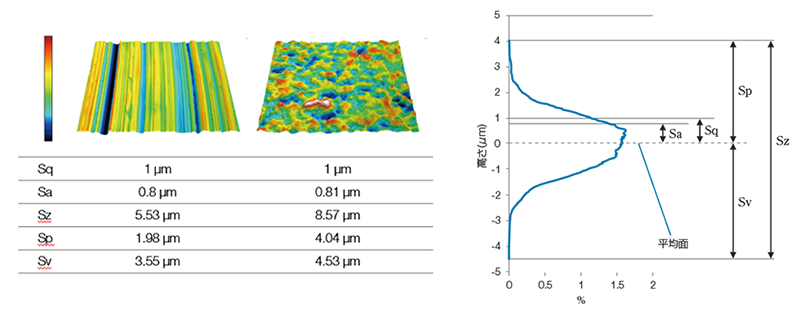
凹凸の大きさを評価したい(Sq、Sa、Sz、Sp、Sv)凹凸の大きさを評価するには高さパラメーター(Sq、Sa、Sz、Sp、Sv)を用います。高さパラメーターはヒストグラム上で下図のような関係になります。 Sq(二乗平均高さ)は高さ分布の標準偏差と同義であり、統計的に取扱い易いパラメーターとして知られています。Sa(算術平均高さ)は平均面からの高低差の平均値です。高さ分布が正規分布の場合、Sa≒0.8*Sqとなる関係があります。 Sz、Sq、Svは高さの最大値や最小値を利用するため、測定ノイズ等により結果が不安定になる場合があります。高さパラメーターは高さの分布情報のみを利用するパラメーターです。従って、水平方向の形状的な特徴はパラメーター値に反映されないことには注意が必要です。
測定事例「自動車内装部品のシボの形状評価」についての詳細はこちら 測定事例「5G向けプリント基板の銅箔の表面粗さ ~Rz(最大高さ)以外の有効な粗さパラメーターの提案」についての詳細はこちら |
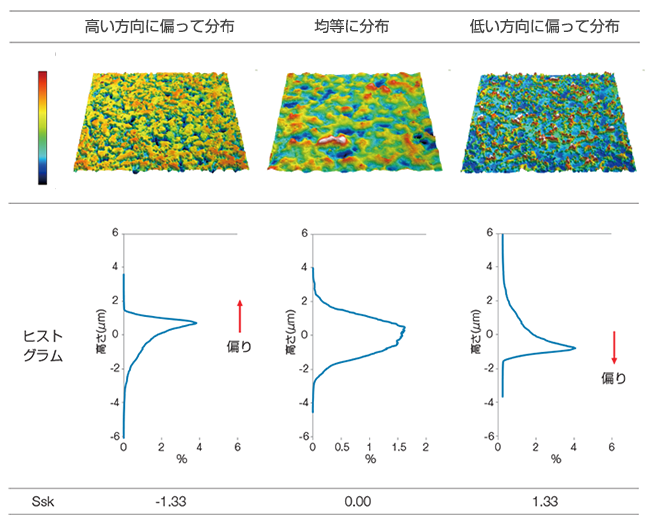
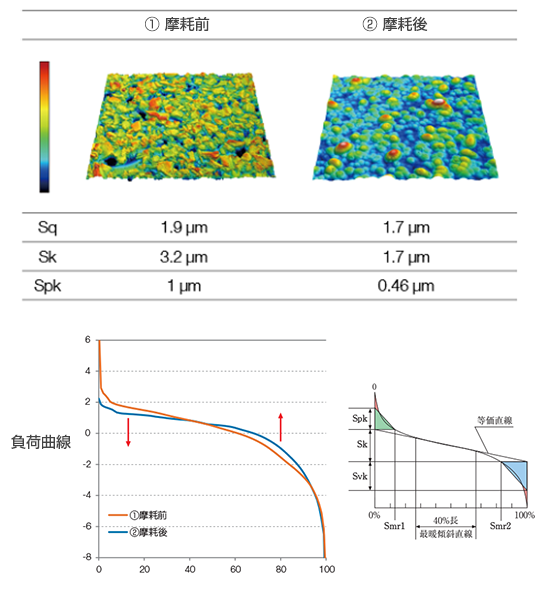
高さの分布を評価したい(Ssk、Sku、ヒストグラム)高さの分布の評価にはヒストグラムの曲線形状を評価するのが一般的です。ヒストグラムの曲線形状(分布)の偏りを評価する指標としてSskパラメーターがあります。 Ssk=0で高低差が均等に分布している状態、マイナス符号で高い方向、プラス符号で低い方向に偏って分布している状態です。摺動摩耗によって高い部分の形状が削られた標本では、Sskはマイナス符号をとる傾向があります。この性質を利用して摩耗度合いの評価指標として利用されることもあります。
|
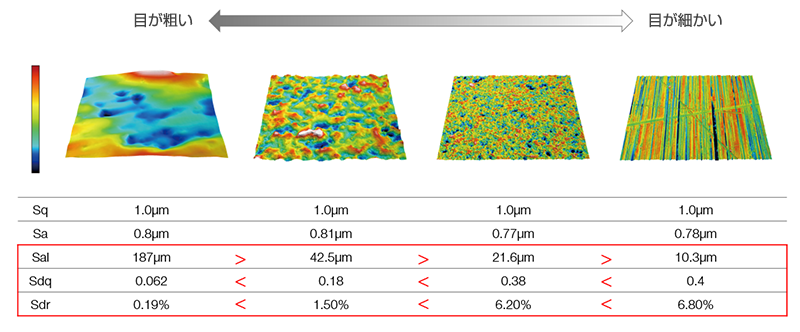
目の細かさを評価したい(Sal、Sdq、Sdr)Salパラメーターは同じような凹凸形状の密集度合いを長さの単位で数値化します。値が小さいほど目が細かいといえます。
測定事例「粗さのパラメーターRa、Saで差が出ない表面形状を別のパラメーターで定量化-スピードメーターカバー防眩性の評価」についての詳細はこちら 測定事例「自動車内装部品のシボの形状評価」についての詳細はこちら 測定事例「5G向けプリント基板の銅箔の表面粗さ ~Rz(最大高さ)以外の有効な粗さパラメーターの提案」についての詳細はこちら |
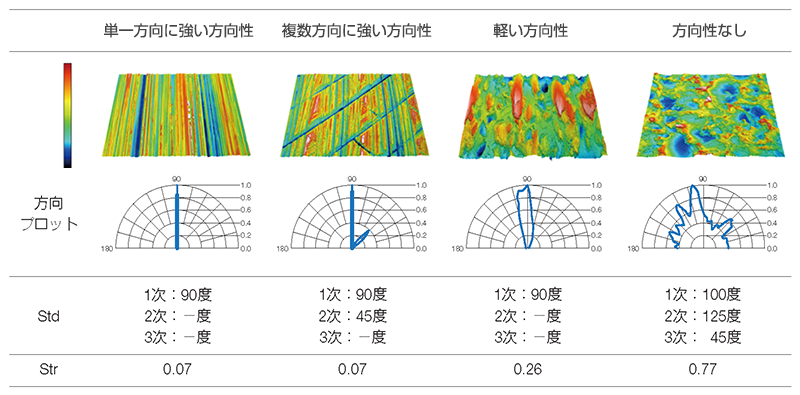
方向性を評価したい(Std、Str、方向プロット)方向性プロットは、表面の方向性を角度チャートで表現したものです。方向性が強いほどピークが鋭くなります。また、最も強いピークが最外周の円に接するように方向性の強さを正規化しています。Stdパラメーターは方向プロットでピークの大きい順番にその角度を示します。
|
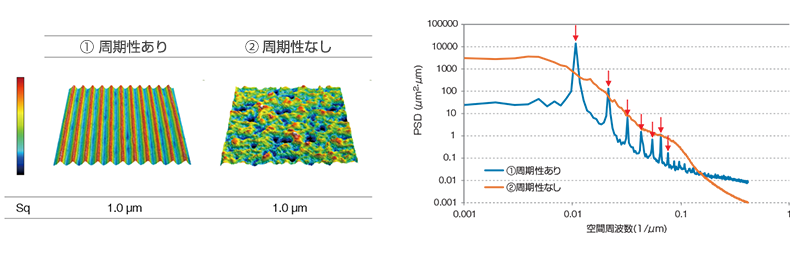
周期性を評価したい(PSD)PSD(パワースペクトル密度)は表面の波長成分ごとの凹凸の大きさを表しています。周期性のある標本ではPSDのグラフにピーク(矢印)が立ちます。ピークの横軸を読みとることとで、周期性の周波数(周期の逆数)を知ることができます。
|
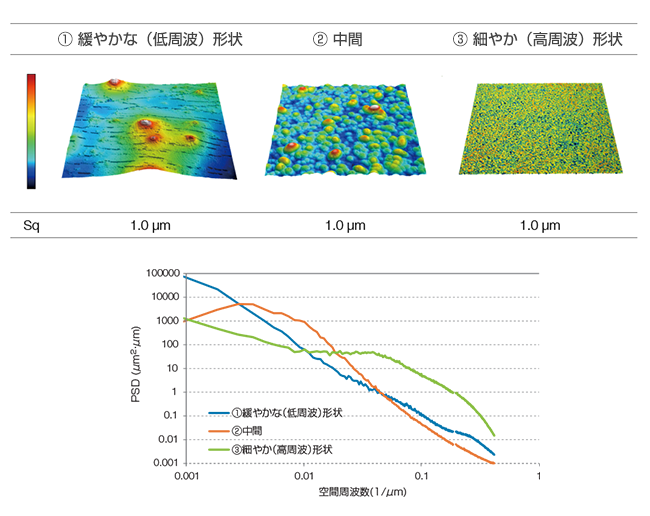
支配的な形状成分を評価したい(PSD)PSD(パワースペクトル密度)は表面の波長成分ごとの凹凸の大きさを表しています。“緩やか”、“細やか”といった形状的な特徴はPSDのグラフにも現れます。
|