包络功能使全聚焦方式更出色
Nicolas Badeau1 Guillaume Painchaud-April1 Alain Le Duff1
1Olympus NDT加拿大公司
3415 Rue Pierre-Ardouin
Quebec QC, G1P 0B3
综述
本文介绍如何计算全聚焦方式(TFM)图像的包络,以及将这种TFM包络用于符合规范的解决方案中可以获得的益处。TFM包络通过计算两个不同TFM图像的范数而获得,具体的说,使用以标准方式获得的全矩阵捕获(FMC)计算第一个TFM图像,使用经过希尔伯特变换的全矩阵捕获(FMC)计算第二个TFM图像。所获得的TFM包络图像为基于波幅的定量方法提供了更好的基础,因为在网格分辨率不变的情况下,这种TFM包络图像比标准的振荡TFM图像,受到波幅变化的影响较少,具有更强的稳定性。因此,可以为TFM包络图像设置一个比标准的振荡TFM图像更粗的网格分辨率,从而可以减少总计算量,并最终提高实际的采集速率。
引言
全聚焦方式(TFM)是一种近来被业界认可的用于材料和结构的无损评估的技术。如今某些标准和规范已经包含了有关用于无损检测(NDT)的全矩阵捕获(FMC)和全聚焦方式(TFM)的章节[1],[2]。
某些NDT设备,如:OmniScan X3探伤仪,可以进行实时TFM成像。下面的小节概括介绍使用全矩阵捕获(FMC)的全聚焦方式(TFM),不过,其基本前提是TFM图像的生成基于大量的基本A扫描波幅值的总和。TFM图像处于振荡状态,因为基本A扫描源于声波。另一方面,NDT应用中的表征方案基本上采用基于波幅的技术,对于这种技术而言,振荡表现会被视为多余的声学伪影。对振荡表现进行调整以使其适用于表征方案的常见做法,是对波幅进行矫正,以使图像完全以正值显示。虽然与完全振荡图像相比,这种方法可能便于对图像进行判读,但是还有一种更好的方法:生成TFM包络图像。本文将说明使用信号包络如何能进一步提高表征效果,以及如何能在实际上获得高于标准振荡TFM图像的采集速率。
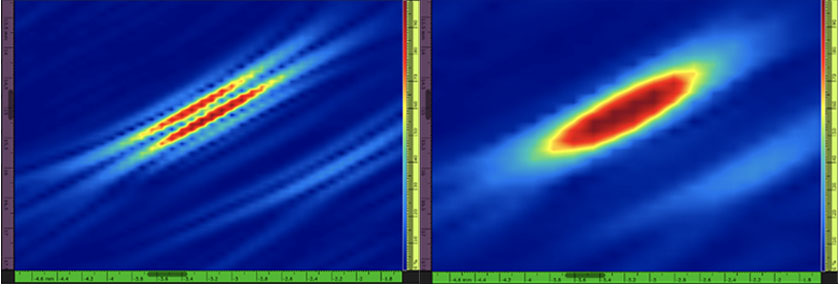
图1 — 左图:一个横通孔(SDH)的TFM图像示例,图像中只有正波幅值,且信号处于振荡状态(这是标准的TFM图像)。 网格分辨率为0.08 mm(λ / 8.1),最大波幅为108.7%。右图:同一个横通孔(SDH)的TFM包络图像。网格分辨率为0.16 mm(λ / 4.0),最大波幅为122.6%。
使用这种震荡TFM图像有多个缺点。首先,TFM网格分辨率,即图像中两个像素之间的距离,必须大约为λ / 8,才会符合规范的要求 [1]–[3]。在本文中,λ是与探头中心频率和工件的声速相关的波长。使用较小的网格分辨率,意味着要进行大量的计算,进而会即刻降低采集速率。与基于波幅的缺陷定量方法相关的稳定性也会受到振荡TFM的影响。实际上,测量到的回波的最大波幅在很大程度上取决于所采集信号的相位偏移。
所有这些问题都可以通过使用TFM包络来解决,因为包络不仅可消除图像中的信号振荡,还可以进行更稳定的最大波幅测量(参见图1)。使用TFM包络可以提高采集效率,因为与标准TFM相比,要获得同样稳定的波幅,TFM包络所需的网格分辨率可以更粗,即两个相邻像素之间的间距更大。例如:要获得相同的波幅保真值(2 dB),TFM包络只需一个约为λ / 4的网格分辨率就够了,而标准振荡TFM却需要λ / 8的分辨率 [3]。
撰写本篇论文的目的是让NDT专家了解使用TFM包络的益处。首先我们扼要陈述一下FMC-TFM方法,然后再简要介绍几个有关TFM包络计算的概念。最后,我们通过将TFM包络图像与标准振荡型TFM图像进行比较,说明将TFM包络用于符合规范的解决方案中的益处。
FMC-TFM方法的综述
超声相控阵技术的标志是在被测工件中任何所需关注的区域聚焦的能力。相控阵聚焦方法在发射脉冲和接收信号时都使用延迟,以使短脉冲信号的渡越时间在所需关注的位置处实现同步。在样件的聚焦区域,所生成声束的总宽度变小,且相应的检测分辨率显著提高 [4]–[12]。
TFM是这种能力的自然扩展;TFM通过在被测工件内关注区域的每个位置上实现相控阵聚焦和偏转,生成聚焦声束,而且只将一组以高分辨率聚焦的数据点呈现给操作人员 [13][16]。通常,关注区域由一个可以标注所有要求的聚焦目标的统一的笛卡尔网格体现。显然,使用传统的物理声束形成方法在每个网格位置实现这种聚焦,会耗费大量的时间,因为要使声波达到每个关注位置,需要大量的物理声束传播时间。
由于NDT应用中所使用的典型超声波具有线性特点,因此可以通过一种基于全矩阵捕获(FMC)数据集的后采集处理,模拟将某个给定孔径所有参与晶片的实际声场叠加在一起而形成物理声束的过程。要检索FMC数据集,就需要在构成发射孔径的每个单独晶片发射脉冲声波时,记录来自构成接收孔径的所有晶片的信号。因此,FMC数据集是由发射晶片和接收晶片的所有组合而生成的许许多多的基本A扫描组成。
正如传统的聚焦相控阵一样,要获得某个给定聚焦位置的聚焦声波的波幅,需要进行以下操作:
- 计算声束传播所需的渡越时间,渡越时间包括声波到达与所选关注网格位置对应的聚焦位置的时间,以及声波返回到接收晶片的时间,而且要为孔径中所有成对的发射晶片和接收晶片所生成的声束计算渡越时间。
- 为孔径中所有成对的发射和接收晶片选择对应于适当的完整发射-接收渡越时间的波幅数据点。
- 将发射和接收孔径的所有参与晶片的所有选定的波幅数据点汇总起来。
- 在最初选定的网格位置上放置所获得的汇总波幅。
为关注区域中的所有网格位置重复上述操作,就会生成一个波幅图,图中的所有波幅值都对应一个聚焦声束,既包含发射声束也包含接收声束。这种使用FMC数据生成一种可以表现关注区域(即TFM区域)中每个位置的聚焦情况的波幅图的方法被称为FMC-TFM方法。
如何计算TFM包络
本节介绍如何使用基本A扫描(FMC)计算TFM包络(要生成标准TFM图像,需要采集相同的基本A扫描)。应该注意的是,包络具有物理表现,而不仅仅是一种图像平滑算法。TFM图像中包络的根源存在于构成图像的单个A扫描中。首先,为了通过示意图形式对包络的表现进行说明,我们使用一个高斯脉冲时间序列介绍包络概念。处理过程也适用于一帧完整TFM图像中的一个经验A扫描。
信号a(t)代表采集到的信号,相当于通过FMC获得的一个基本A扫描,实际上,就是复杂分析信号z(t)的实部,可以表达为以下等式:

其中a’(t)对应于分析信号的虚部,而θ(t)是信号的瞬时相位。通过使用希尔伯特变换可以有效地计算出虚部[17]。信号包络对应于分析信号的范数,可以表达为下列等式:
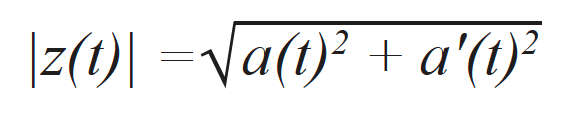
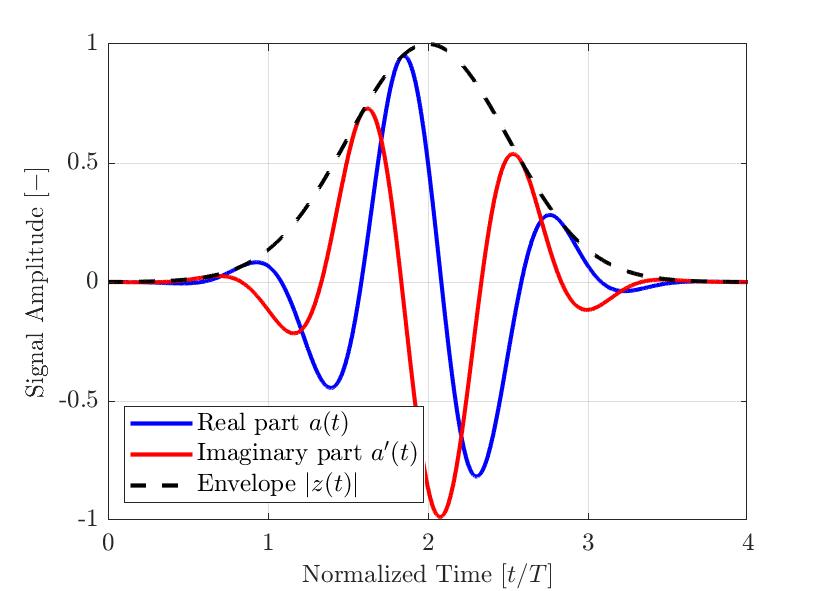
图 2 — 用于NDT应用的典型高斯调制脉冲。图中显示了实部、虚部和通过计算而获得的包络。时间轴根据脉冲的选定中心频率周期得到归一化。
图2是一个简单的高斯调制脉冲a(t)的示例。真实信号a(t)是蓝色线,其经过希尔伯特变换的虚部a’(t)是红色线,通过计算而获得的包络|z(t)|是虚线。如上面的等式所示,信号包络|z(t)|不受信号瞬时相位θ(t)的影响。因此,具有不同相位偏移ϕ的信号可以具有相同的包络。图3显示的是几个具有不同相位偏移ϕ的高斯调制脉冲,以及它们的包络。因此,在使用信号包络时,所测到的信号最大波幅,比分析信号实部的绝对值更稳定可靠。
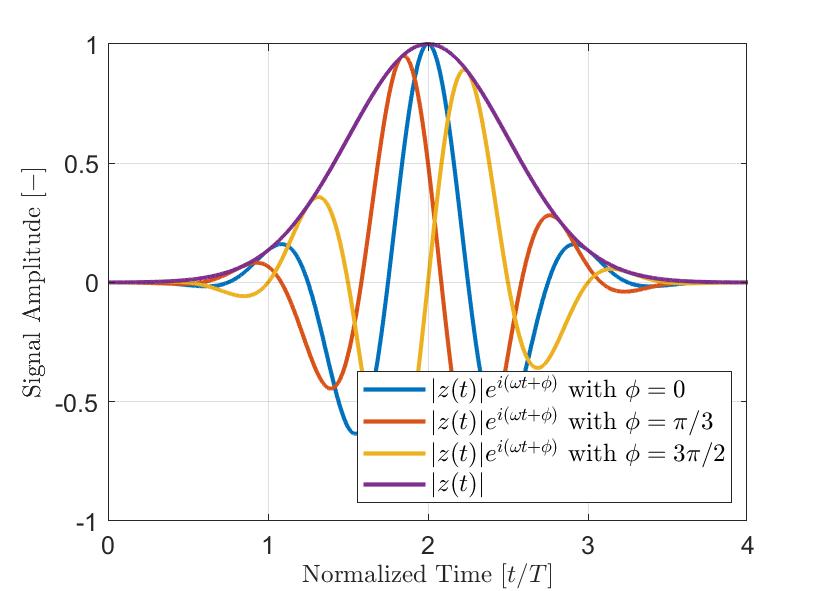
图 3 — 带有不同相位偏移ϕ的典型的高斯调制脉冲(|z(t)|ei(ωt+ϕ))。显而易见,信号的包络|z(t)|独立于分析信号的瞬时相位。
同样的过程也可以用于获得经验A扫描的包络。图4显示的是一个通过FMC获得的典型的基本A扫描,而图5中显示了与图4相同的A扫描(蓝线),经过希尔伯特变换的虚部(红线)和计算得到的包络(虚线)。图中显示的所有信号都被归一化为波幅包络的最大值。
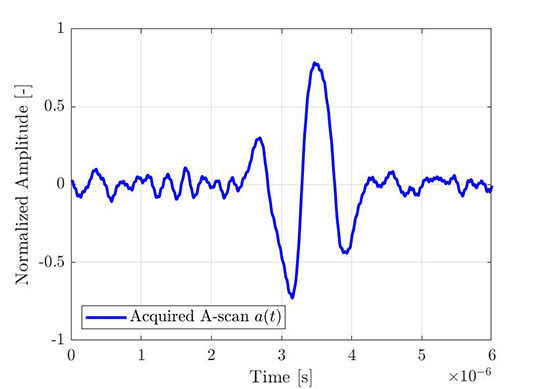 图 4 — 所获得的基本A扫描的一部分(来自FMC采集)。 | 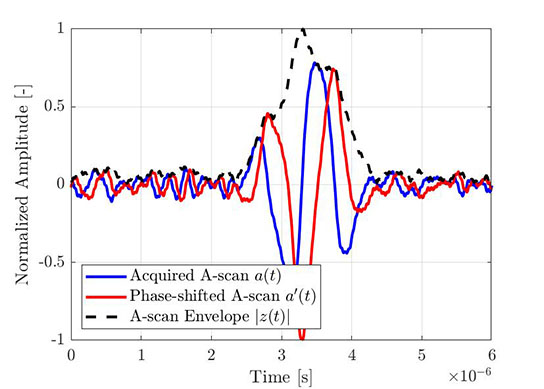 图 5:相同的基本A扫描,及其经过希尔伯特变换的信号虚部和计算出的包络。 |
带有单个网格点索引(k,l)的TFM包络图像,通过对来自构成图像的所有A扫描的分析信号进行计算而获得 [15]。事实上,这个结果通过计算分析型TFM图像y(k,l)的范数而获得,包括由使用标准FMC采集的数据计算的标准TFM图像x(k,l),和通过对FMC数据进行希尔伯特变换而计算的TFM图像x'(k,l)。两种情况使用同一组延迟值。然后使用以下表达式计算TFM包络:
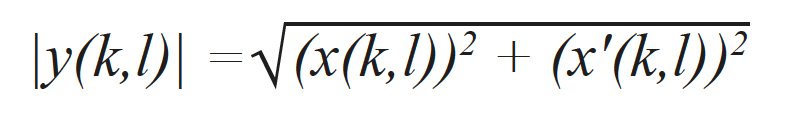
因此,我们可以说,TFM包络图像是将两个TFM图像组合在一起得到的结果(参见图6):一个图像来自基本A扫描的实部,另一个图像来自计算获得的基本A扫描的虚部。虽然这个过程增加了计算负担,也会降低NDT仪器的采集速度,但是却可以获得我们在下一节中将说明的优势:大幅降低所需的网格分辨率,而不会影响波幅保真值,从而可以提高采集速率,使其比使用标准TFM进行检测的速度还要快。
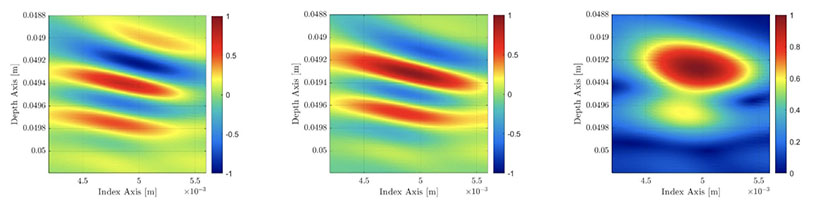
图 6 — 左图:标准TFM图像(非绝对值形式)。中图:通过为FMC进行希尔伯特转换而计算获得的TFM图像。右图:获得的TFM包络图像。
使用TFM包络的优势
在本节中,我们说明TFM包络的优势,方法是对比几个具有不同网格分辨率比(从λ / 9.3到λ / 4.0)的TFM图像,并监控图像中各种关键性检测指标。这些图像是我们使用5L32-A31探头和SA31-N55S-IHC楔块在一个带有1毫米直径横通孔(SDH)的钢块上进行扫查而获得(见图7)。在楔块和钢块之间使用了一种耦合凝胶(Sonotech Ultragel II)。使用奥林巴斯的OmniScan X3探伤仪采集检测数据。我们为检测选用了脉冲回波(T-T)声程,区域大小为(20 mm × 20 mm)。与工件和所选声程相关的波长为λ = 0.648 mm。网格分辨率以波长的分数表示。

图 7 — 用于采集表1中的TFM图像的设置。蓝色矩形框对应于整个关注区域(20 mm × 20 mm),而红色矩形框对应于表1的图像中显示的放大的局部关注区域(5 mm × 5 mm)。我们使用了5L32-A31探头和SA31-N55S-IHC楔块。钢块的厚度为40 mm。
表1中显示了分别使用4个不同的网格分辨率(范围从λ / 9.3到λ / 4.0)所获得的标准TFM图像和TFM包络图像。每个TFM图像中标出了计算出的波幅保真值[3]和实际获得的采集速率。
网格分辨率 | 标准TFM图像 | TFM包络图像 |
|---|---|---|
λ / 9.3 | 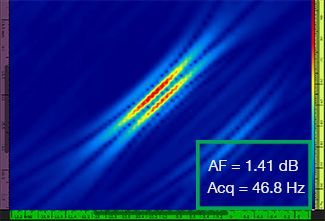 | 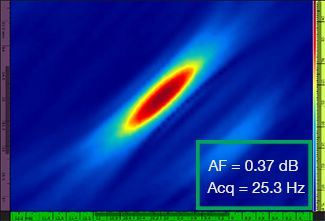 |
λ / 8.1 | 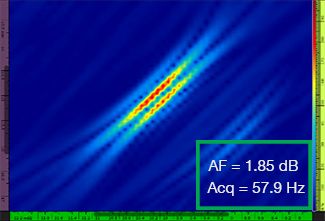 | 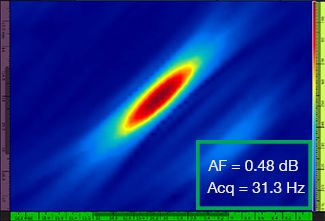 |
λ / 5.9 | 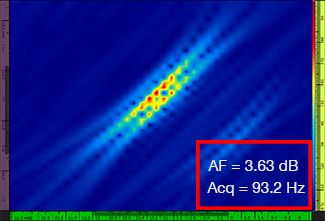 | 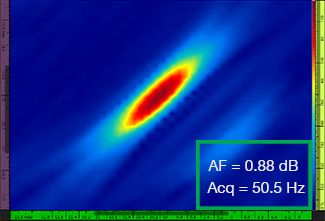 |
λ / 4.0 |  |  |
表 1 — 比较使用四个不同网格分辨率值所获得的标准TFM图像和TFM包络图像的质量。这些图像为放大后的TFM图像。图中的文字AF代表波幅保真值,Acq代表在特定网格分辨率下获得的采集速率。红色边框表明图像没有达到规范所要求的2 dB波幅保真值。请注意在波幅保真值大致相同的情况下具有较高采集速率的图像。
新出台的规范和标准[1,2]要求波幅保真值等于或低于2 dB。因此,4个标准TFM图像中,只有前两个图像的网格分辨率值(分别为λ / 9.3和λ / 8.1)符合规范的要求。TFM包络可在使图像的波幅保真值持续符合规范要求的同时,使用更粗的网格分辨率(λ / 4.0)。进而,在使用一个较粗网格分辨率的TFM包络图像时,与符合规范的标准TFM图像可达到的最高采集速率(分辨率为λ / 8.1时,采集速率为57.9 Hz)相比,可以将采集速率提高约37%。
结论
本文通过简单的示例说明了计算TFM图像包络的方法。我们证明了信号的包络不受其瞬时相位影响,因此,可以为基于波幅的定量技术(如:6 dB下降法)提供一个更为稳定的基础。信号包络不仅仅是图像平滑,也不应被视为一种可能会造成数据丢失的滤波设置。通过比较使用包络和未使用包络的TFM图像在应用不同网格分辨率时的表现,证明了在TFM成像中使用包络的优势。虽然为了获得TFM包络,必须要对两种TFM图像进行计算,但是采用更粗的网格分辨率可以大幅减少数据处理的负担,同时还可使波幅保真值符合规范的要求。这是因为包络相对于波幅的变化具有稳定性。与经过处理后获得的等效标准TFM图像相比,这种使用了包络的图像可以更快的速度进行采集,而且更适用于波幅定量检测。
参考文献
[1] 美国机械工程师协会(ASME)委员会,“ASME BPVC.V Article 4 Mandatory Appendix XI Full Matric Capture”,ASME,2019年。
[2] 美国机械工程师协会(ASME)委员会,“ASME BPVC.V Article 4 Nonmandatory Appendix F - Examination of Welds Using Full Matric Capture”,ASME,2019年。
[3] N. Badeau、A. Le Duff和C.-H. Kwan,“Theoretical Model for Amplitude Fidelity Reading (submitted)”,发表于ASNT研讨会,2020年。
[4] A. C. Clay、S.-C. Wooh、L. Azar和J.-Y. Wang,“Experimental Study of Phased Array Beam Steering Characteristics”,Journal of Nondestructive Evaluation(《无损评估杂志》),第18卷,第2期,第13页,1999年。
[5] L. J. Bond,“Fundamentals of Ultrasonic Inspection,” ASM Handbook(《ASM手册》),第17卷,材料的无损评估,第155–168页,2018年。
[6] S.-J. Song、H. J. Shin和Y. H. Jang,“Development of an ultra sonic phased array system for nondestructive tests of nuclear power plant components”,Nuclear Engineering and Design(《核工程与设计》),第214卷,第1–2期,第151–161页,2002年5月,doi: 10.1016/S0029-5493(02)00024-9。
[7] S. Mahaut、O. Roy、C. Beroni和B. Rotter,“Development of phased array techniques to improve characterization of defect located in a component of complex geometry”,Ultrasonics(《超声学》),第40卷,第1–8期,第165–169页,2002年5月,doi: 10.1016/S0041-624X(02)00131-2。
[8] S. C. Mondal、P. D. Wilcox和B. W. Drinkwater,“Design of Two-Dimensional Ultrasonic Phased Array Transducers”,Journal of Pressure Vessel Technology(《压力容器技术杂志》),第127卷,第3期,第336–344页,2005年8月,doi: 10.1115/1.1991873。
[9] S.-C. Wooh和Y. Shi,“Influence of phased array element size on beam steering behavior”,Ultrasonics(《超声学》),第36卷,第6期,第737–749页,1998年4月,doi: 10.1016/S0041-624X(97)00164-9。
[10] Joon-Hyun Lee和Sang-Woo Choi,“A parametric study of ultrasonic beam profiles for a linear phased array transducer”,IEEE Trans. Ultrason., Ferroelect., Freq. Contr.(《IEEE超声、铁电和频率控制学报》),第47卷,第3期,第644–650页,2000年5月,doi: 10.1109/58.842052。
[11] R. Ahmad、T. Kundu和D. Placko,“Modeling of phased array transducers”,The Journal of the Acoustical Society of America(《美国声学协会杂志》),第117卷,第4期,第1762–1776页,2005年4月,doi: 10.1121/1.1835506。
[12] B. W. Drinkwater和P. D. Wilcox,“Ultrasonic arrays for non-destructive evaluation: A review”,NDT & E International(《国际无损检测与评估》),第39卷,第7期,第525–541页,2006年10月,doi: 10.1016/j.ndteint.2006.03.006。
[13] P. D. Wilcox,“Exploiting the Full Data Set from Ultrasonic Arrays by Post-Processing”,AIP Conference Proceedings(《AIP会议记录》),Brunswick,Maine(美国缅因州),2006年,第820卷,第845–852页,doi: 10.1063/1.2184614。
[14] J. Zhang、B. W. Drinkwater和P. D. Wilcox,“Effects of array transducer inconsistencies on total focusing method imaging performance”,NDT & E International(《国际无损检测与评估》),第44卷,第4期,第361–368页,2011年7月,doi: 10.1016/j.ndteint.2011.03.001。
[15] C. Holmes、B. W. Drinkwater和P. D. Wilcox,“Advanced post-processing for scanned ultrasonic arrays: Application to defect detection and classification in non-destructive evaluation”,Ultrasonics(《超声学》),第48卷,第6–7期,第636–642页,2008年11月,doi: 10.1016/j.ultras.2008.07.019。
[16] C. Holmes、B. W. Drinkwater和P. D. Wilcox,“Post-processing of the full matrix of ultrasonic transmit–receive array data for non-destructive evaluation”,NDT & E International(《国际无损检测与评估》),第38卷,第8期,第701–711页,2005年12月,doi: 10.1016/j.ndteint.2005.04.002。
[17] D. Gabor,“Theory of Communication”,Journal of the Institution of Electrical Engineers(《电气工程学会杂志》),第96卷,第429–441页,1946年。