常规探头的波前动态属性
Formação da inclinação da onda
Enquanto um transdutor de elemento único pode ser descrito como uma fonte de pistão, um disco único ou uma placa de impulso em testes, as ondas geradas podem ser modeladas matematicamente como um resumo de ondas de uma quantidade muito grande de fontes de pontos. Isso é derivado do Princípio de Huygens, proposto pela primeira vez pelo físico holandês Christiaan Huygens no século XVII, que afirma que cada ponto em uma frente de onda em avanço pode ser pensado como uma fonte pontual que lança uma nova onda esférica e que a frente de onda unificada resultante é a soma de todas essas ondas esféricas individuais.
Propagação do feixe
Em princípio, a onda de som gerada por um transdutor viaja em linha reta até encontrar uma margem física. O que acorre em seguido é discutido abaixo. Mas se o comprimento do trajeto do som é maior que a distância do campo próximo, o diâmetro do feixe também aumentará, como o feixe divergente de um refletor. O ângulo de propagação do feixe de um transdutor desfocado pode ser calculado da seguinte forma:

A partir desta equação, pode-se ver que a propagação do feixe aumenta com a redução da frequência e diâmetros menores. Como um grande ângulo de dispersão do feixe pode fazer com que a energia do som por unidade de área diminua rapidamente com a distância, diminuindo efetivamente a sensibilidade a pequenos refletores, a resposta do eco em algumas aplicações que envolvem longos trajetos sonoros pode ser melhorada usando transdutores de frequência mais alta e/ou diâmetro maior.
Atenuação
À medida que viaja através de um meio, a frente de onda organizada gerada por um transdutor ultrassônico começará a quebrar devido à transmissão imperfeita de energia através da microestrutura de qualquer material. As vibrações mecânicas organizadas (ondas sonoras) transformam-se em vibrações mecânicas aleatórias (calor) até que a inclinação da onda deixa de ser detectável. Este processo é conhecido como atenuação do som.
A teoria matemática da atenuação e propagação é complexa. A perda de amplitude devido à atenuação em um determinado trajeto sonoro será a soma dos efeitos de absorção, que aumentam linearmente com a frequência, e os efeitos de propagação, que variam em três zonas, dependendo da proporção do tamanho dos limites de grãos ou de outros dispersores em relação ao comprimento da onda. Em todos os casos, os efeitos da propagação aumentam com a frequência. Para uma dado material a uma temperatura dada, testado com uma dada frequência, haverá um coeficiente de atenuação específico, normalmente expresso em Neperes por centímetro (Np/cm). Uma vez que o coeficiente da atenuação é conhecido, as perdas através de uma trajetória de som determinada podem ser calculadas de acordo com a equação.

Por uma questão prática, os coeficientes de atenuação para aplicações de ultrassom para END, normalmente são medidas em vez de serem calculadas. As frequências mais altas serão atenuadas mais rapidamente que as frequências mais baixas em qualquer meio, os testes com baixa frequência são normalmente empregados em materiais com altos índices de atenuação, como plásticos de baixa densidade e borracha.
Reflexão e transmissão em uma margem do plano perpendicular
Quando uma onda sonora que viaja através de um meio encontra um limite com um meio diferente perpendicular à direção da onda, uma porção da energia da onda é refletida diretamente para trás e uma parte continua em frente. A porcentagem de reflexão em relação à transmissão está relacionada às impedâncias acústicas relativas dos dois materiais, sendo a impedância acústica, por sua vez, definida como a densidade do material multiplicada pela velocidade do som. O coeficiente de reflexão em um limite plano, a porcentagem de energia sonora que é refletida de volta à fonte, pode ser calculada da seguinte forma:

A partir desta equação, pode-se observar que, à medida que as impedâncias acústicas dos dois materiais se tornam mais semelhantes, o coeficiente de reflexão diminui e, à medida que as impedâncias acústicas se tornam menos semelhantes, o coeficiente de reflexão aumenta. Em teoria, a reflexão do limite entre dois materiais da mesma impedância acústica é zero, enquanto no caso de materiais com impedâncias acústicas muito diferentes, como no limite entre aço e ar, o coeficiente de reflexão se aproxima de 100%.
Refração e modo de conversão em margens não perpendiculares
Quando uma onda sonora se propaga através de um material e encontra um limite com um material diferente em um ângulo diferente de zero, uma porção da energia da onda será refletida com um ângulo igual ao ângulo de incidência. Ao mesmo tempo, a porção da energia das ondas que é transmitida para o segundo material será refratada de acordo com a Lei de Snell, obtida independentemente por pelo menos dois matemáticos do século XVII. A lei de Snell relaciona os senos de incidência e o ângulo refratado à velocidade da onda em cada material como demonstrado abaixo.
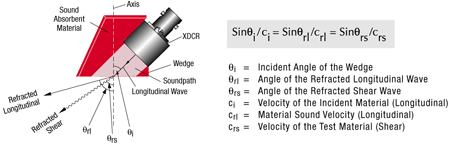
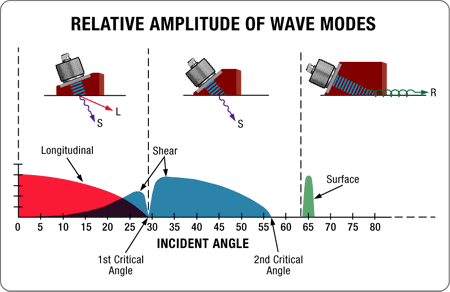
Se a velocidade do som no segundo meio for maior que a do primeiro, então acima de certos ângulos, essa flexão será acompanhada pela conversão do modo, mais comumente do modo de onda longitudinal para o modo de onda de cisalhamento. Essas são as técnicas básicas de inspeção de feixe angular amplamente utilizadas. À medida que o ângulo de incidência no primeiro meio (mais lento), como um calço ou água, aumenta, o ângulo da onda longitudinal refratada no segundo material (mais rápido), como o metal, aumenta. Conforme o ângulo longitudinal refratado da onda se aproxima de 90 graus, uma porção progressivamente maior da energia da onda será convertida em uma onda de cisalhamento de velocidade mais baixa que será refratada no ângulo previsto pela Lei de Snell. Em ângulos de incidência superiores aos que criaria uma onda longitudinal refratada a 90 graus, a onda refratada existe inteiramente no modo de cisalhamento. Um ângulo de incidência ainda mais alto resultará em uma situação em que a onda de cisalhamento é teoricamente refratada a 90 graus, momento esse em que uma onda de superfície é gerada no segundo material. O diagrama abaixo mostra esse efeito para um conjunto de feixe de ângulo típico acoplado ao aço.