全聚焦方式声学影响图

Chi-Hang Kwan
Guillaume Painchaud-April
Benoit Lepage
Artigo apresentado originalmente no Simpósio de Pesquisa ASNT, 2019.

RESUMO

Neste artigo, apresentamos um modelo semianalítico recém-desenvolvido para antever o mapa de sensibilidade à amplitude do método de foco total (TFM) para falhas não direcionais e direcionais. Para trajetos acústicos complicados que envolvem várias interações de interface e conversões no modo de onda, o conhecimento do Mapa de Influência Acústica (AIM) permite que o inspetor aperfeiçoe o plano de varredura para maximizar a relação de sinal-ruído da imagem TFM resultante e aumentar a probabilidade de detecção de falhas. A precisão desse novo modelo acústico foi testada e validada por experimentos usando blocos de teste que contêm orifícios laterais perfurados (SDH) e orifícios de fundo plano (FBH). Os resultados dos experimentos de validação mostram boa concordância entre os mapas empíricos de amplitude do TFM e o AIM teórico. Os resultados também indicam que o modelo pode ser usado para orientar a seleção do modo de inspeção TFM ideal.

INTRODUÇÃO

O método de foco total (TFM) é uma técnica de formação de feixe de abertura sintética que esteve em desenvolvimento ativo na indústria de END durante a última década [1]. Ao aplicar atrasos de transmissão e recepção apropriados aos dados dos A-scan coletados em um conjunto de dados de captura completa de matriz (FMC), o TFM pode concentrar-se eletronicamente em todos os locais de uma região de inspeção. Como todos os pontos são eletronicamente focados, o TFM pode fornecer melhor resolução quando comparado com as técnicas convencionais de inspeção por ultrassom Phased Array. Além disso, calculando e aplicando o tempo de voo de vários modos acústicos, o TFM multimodo pode fornecer informações adicionais sobre a amostra que está sendo inspecionada [2].

Apesar das vantagens listadas acima, o TFM também possui limitações regidas pelas leis da física. Uma área de inspeção pode ter pouca sensibilidade devido aos efeitos da interação da interface, limitações de formação de feixe e atenuação do trajeto de propagação. Devido à novidade do TFM, à falta de códigos de inspeção e à complexidade da geração de imagens TFM multimodo, os inspetores geralmente desconhecem os limites físicos do TFM e, portanto, não podem definir um plano de varredura ideal que maximize a relação sinal-ruído (SNR) e a probabilidade de detecção. Consequentemente, é necessário introduzir uma ferramenta que prepare o mapa da sensibilidade acústica para um determinado plano de varredura de inspeção TFM.

REGIÃO ACÚSTICA DE INFLUÊNCIA

O Mapa de Influência Acústica (AIM) é um mapa teórico de sensibilidade à amplitude acústica para um determinado plano de varredura de inspeção TFM. Em geral, o AIM difere dos dispersores de falhas direcionais e não direcionais. Os exemplos de END de dispersores não direcionais incluem escória e porosidade nas soldas, enquanto exemplos de dispersores direcionais incluem falta de fusão nas soldas e várias fissuras. A resposta direcional da dispersão de uma falha é um parâmetro importante que é frequentemente negligenciado na modelagem de sistemas de transdutores Phased Array.

Para calcular o AIM, desenvolvemos um modelo acústico semianalítico baseado em raios que calcula a resposta da pressão bidirecional dos modos de inspeção TFM com pulso-eco, auto-tandem e salto duplo. Esse modelo acústico leva em consideração os efeitos dos coeficientes de transmissão e reflexão, da difusão do feixe geométrico e da atenuação do material. Além disso, em nosso modelo, também usamos a integral de Rayleigh-Sommerfeld [3] para esboçar a resposta da dispersão de campo distante de orifício de fundo plano (FBH). A resposta da dispersão do FBH é usada para simular falhas direcionais.

EXPERIÊNCIAS DE VALIDAÇÃO Para examinar a precisão do modelo acústico, realizamos experimentos de validação para comparar mapas de amplitude de TFM obtidos experimentalmente com um mapa de sensibilidade acústica do TFM calculado teoricamente. Os resultados obtidos nas duas experiências de validação são apresentados nesta seção. O primeiro experimento de validação foi realizado em um bloco de teste com furos laterais de pequeno diâmetro (SDH), que simulam a resposta da dispersão dos dispersores de falhas não direcionais. O segundo experimento de validação foi realizado em um bloco de teste que contém FBH, que simula a resposta de dispersão de falhas direcionais. Para os resultados apresentados neste artigo, o eixo x é definido como positivo à direita do primeiro elemento do transdutor e o eixo z é definido como positivo abaixo da superfície da amostra de teste. O diagrama esquemático desse sistema de coordenadas é mostrado na figura 1.

Figura 1: Sistema de coordenadas usado neste artigo.

Validação de orifício lateral perfurado (SDH)

A experiência de validação do SDH foi conduzida em um bloco de teste métrico de aço 1018 NAVSHIPS que contém seis SDH de 1,2 mm (0,05 pol.) de diâmetro em profundidades de 6,25 mm (0,25 pol.) a 37,5 mm (1,5 pol.) com incrementos de 6,25 mm. Virando o bloco de teste, é possível examinar o SDH em profundidades de 6,25 mm (0,25 pol.) a 68,75 mm (2,7 pol.). Para esse experimento, usamos uma sonda 5L32-A31 de 32 elementos com frequência central de 5 MHz e elemento com pitch de 0,6 mm. A sonda foi acoplada a um calço Rexolite SA31-N55S-IHC de 36,1º. O esquema da configuração experimental é mostrado na figura 2.

Figura 2: Diagrama esquemático do experimento de validação de SDH. Note que apenas a orientação superior da varredura é mostrada.

Ao passar a sonda ao longo da superfície do bloco de teste, obtivemos ecos de dispersão dos SDH em diferentes posições em relação à sonda. Os conjuntos de dados FMC foram coletados em cada posição de varredura para pós-processamento para gerar mapas empíricos de amplitude do TFM. A descrição do algoritmo de pós-processamento é apresentada na subseção a seguir.

Criação do mapa empírico de amplitude do TFM

As principais etapas para gerar o mapa empírico de amplitude do TFM são:

• Para uma determinada falha em uma posição fixa de varredura, use uma porta de profundidade (direção z) para obter uma linha de amplitude ao longo da largura do mapa de amplitude.
• Repita a etapa 1 em diferentes posições de varredura para obter uma linha de amplitude composta para uma determinada falha.
• Repita as etapas 1 e 2 para todas as outras falhas e obter as linhas de amplitude composta em diferentes posições z.
• Interpole as linhas de amplitude composta na direção z para obter o mapa de amplitude final do TFM.

A etapa 1 é ilustrada na figura 3. A figura 3 mostra que primeiro estabelecemos uma faixa TFM ao longo da largura do mapa de amplitude nas profundidades especificadas pela porta Z. A posição da porta Z é escolhida com base na profundidade conhecida da falha. Em todas as posições x ao longo da faixa TFM, a amplitude máxima é obtida ao longo da direção z para obter a linha de amplitude mostrada na parte inferior da figura 3.

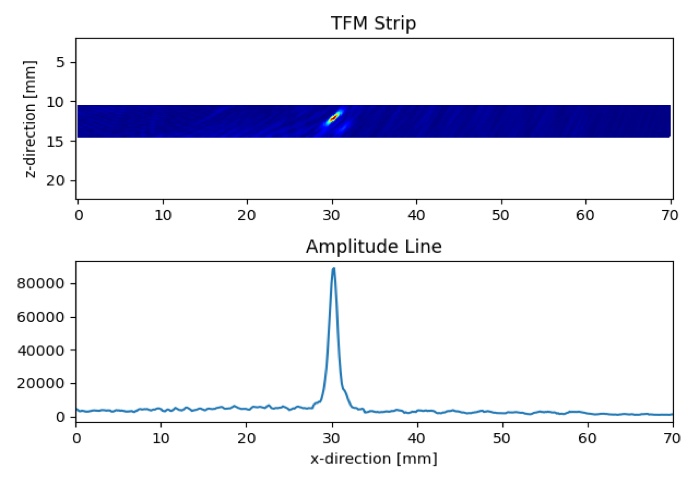
Figura 3: Procedimento para obter uma linha de amplitude para uma determinada falha em uma posição de varredura

Para formar a linha de amplitude composta para uma determinada falha, comparamos todas as linhas de amplitude obtidas em diferentes posições de varredura e registramos os valores máximos de amplitude. Esse procedimento é ilustrado na figura 4.

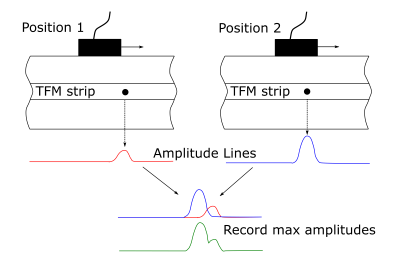
Figura 4: Procedimento para formar linhas de amplitude compostas em diferentes posições de varredura

Após formar a linha de amplitude composta para uma determinada falha, o processo é repetido para todas as falhas em diferentes profundidades. A figura 5 mostra as linhas de amplitude composta no modo TT de pulso-eco obtidas para os SDH presentes no bloco de teste NAVSHIPS (orientações superior e inferior). Na figura 5 e em todas as outras figuras experimentais derivadas de TFM apresentadas neste artigo, as amplitudes das imagens TFM não são normalizadas. Como um digitalizador de 12 bits é usado nos componentes eletrônicos de aquisição e a sonda contém 32 elementos, a amplitude máxima teórica na imagem TFM é de 2.097.152 (212 × 2 × 32 × 32).

Observe que as linhas de amplitude composta para SDH nas profundidades de 6,25 mm (0,25 pol.), 62,5 mm (2,5 pol.) e 68,75 mm (2,7 pol.) não foram incluídas na figura 5. Devido à proximidade desses SDH aos limites laterais do bloco de teste, não foi possível obter linhas completas de amplitude composta ao longo de toda a largura do mapa de amplitude.

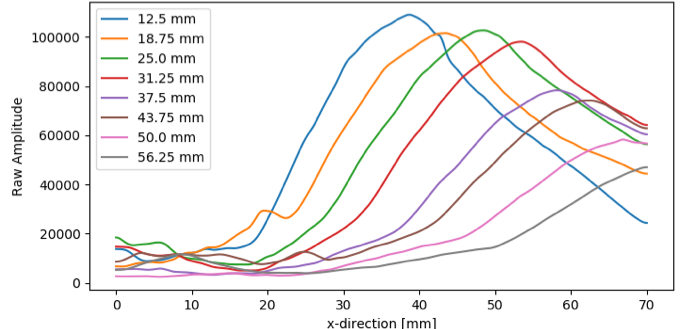
Figura 5: Linhas de amplitude composta de SDH presentes no bloco de teste NAVSHIPS

Comparando os mapas empíricos de amplitude TFM com o AIM

Executando a interpolação na direção z nas linhas de amplitude composta mostradas na figura 5, obtivemos o mapa empírico de amplitude de TFM mostrado na figura 6 (a).

A figura 6 (a) mostra que esse plano de varredura do TFM apresenta baixa sensibilidade tanto em ângulos de direção baixos (30º) como altos (> 70º). A baixa sensibilidade em baixos ângulos de direção é causada por pequenos valores do coeficiente de transmissão do calço Rexolite ao bloco de teste de aço [4]. Por outro lado, a baixa sensibilidade em altos ângulos de direção deve-se à baixa focagem causada por grandes números F efetivos [5]. Esses achados são consistentes com as diretrizes recomendadas para ângulos de direção para inspeções angulares de Phased Array convencional [6].

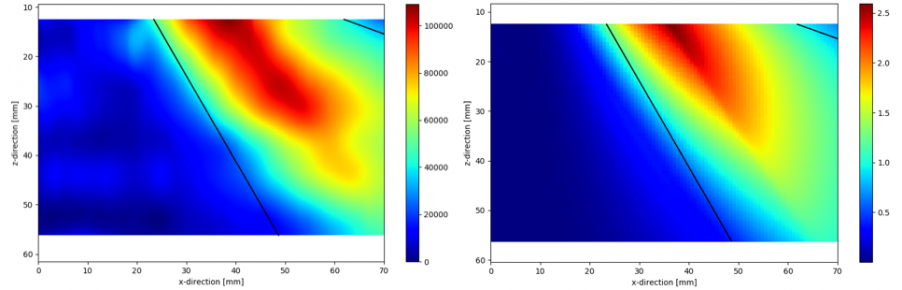
Figura 6: (a) mapa empírico da amplitude do SDH; (b) mapa da sensibilidade da amplitude teórico do SDH no modo TT com pulso-eco. Foram adicionadas diretrizes de ângulo de direção de 30º e 70º (a partir do ponto médio da abertura ativa). O AIM teórico correspondente do SDH é mostrado na figura 6 (b).

Ao comparar as figuras 6 (a) e (b), fica evidente que o modelo acústico pode prever com precisão a área dentro do plano de varredura que possui a sensibilidade ideal. As discrepâncias entre as duas figuras podem ser atribuídas a pequenas variações na pressão de acoplamento, à medida que a sonda é passada pela superfície do bloco de teste. Observe que a amplitude do objetivo teórico está em unidades arbitrárias, porque é extremamente difícil modelar a magnitude exata dos sinais de tensão recebidos do sistema de aquisição. No entanto, como unidades arbitrárias consistentes são usadas para diferentes objetivos, ainda é possível comparar as sensibilidades acústicas do TFM de diferentes planos de varredura e diferentes modos acústicos.

Validação de orifício em fundo plano (FBH)

Para testar a precisão do modelo acústico e prever a sensibilidade da amplitude para falhas direcionais, realizamos experimentos de validação em um bloco de teste usinado sob medida. O bloco de teste tem uma espessura de 20 mm (0,8 pol.) e contém FBH que foram perfurados para corresponder ao perfil de uma solda com chanfro típico em J. Para este estudo, usamos os 5 FBH cujos vetores normais da superfície inferior estão orientados a 3º abaixo da horizontal. A fotografia do bloco de teste com indicações dos eixos de varredura é mostrada na figura 7.

Figura 7: Bloco de teste com FBH usinado sob medida, mostrando os eixos de varredura

Para este experimento, usamos a sonda 5L32-A32 de 32 elementos com uma frequência central de 5 MHz e um passo de elemento de 1 mm. A sonda foi acoplada a um calço Rexolite SA32-N55S-IHC de 36,1º. Como as orientações das superfícies inferiores dos FBH estão quase na vertical, os conjuntos de dados FMC adquiridos foram processados nos modos auto-tandem (salto único). Um diagrama esquemático do plano de varredura é mostrado na figura 8.

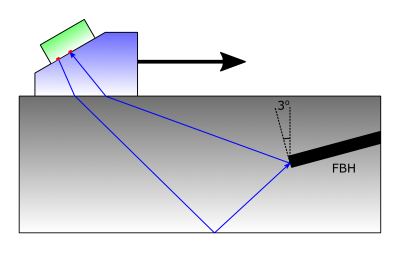
Figura 8: O diagrama esquemático do experimento de validação exibe o modo TFM auto-tandem

Comparando os mapas empíricos de amplitude TFM com o AIM

O mapa empírico de amplitude do FBH e o FBH AIM teórico para o modo TTT auto-tandem são mostrados respectivamente na figura 9 (a) e (b). Ao comparar as duas plotagens, fica evidente que o modelo acústico fornece uma estimativa precisa da sensibilidade acústica relativa na região de varredura. A figura 9 sugere que o TTT auto-tandem é mais adequado para detectar falhas verticais localizadas perto da parte inferior da amostra de teste.

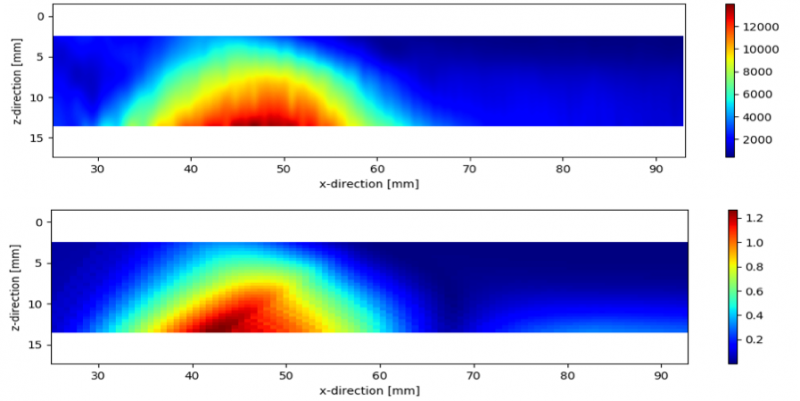
Figura 9: (a) mapa empírico de amplitude da FBH e (b) mapa da sensibilidade da amplitude do FBH para o modo TTT auto-tandem

O mapa empírico de amplitude do FBH e o FBH AIM teórico para o modo TLT auto-tandem são mostrados respectivamente na figura 10 (a) e (b). Mais uma vez, é evidente que o modelo acústico fornece uma estimativa precisa da sensibilidade acústica relativa na região de varredura. As oscilações da amplitude empírica são mapeadas de x = 25 mm (1 pol.) até x = 40 mm (1,6 pol.) e são causados por interferência de outros modos acústicos que possuem tempos de deslocamento semelhantes.

Além disso, comparando a figura 9 com a figura 10, vemos que as proporções de amplitudes máximas entre os dois modos auto-tandem são de aproximadamente 3,3 (13.800/4.200), para os mapas de amplitude empírica, e de aproximadamente 3,4 (1,23/0,36), para o mapa de sensibilidade da amplitude teórico. A similaridade nas proporções de amplitude sugere que o modelo acústico também pode ser usado para prever a sensibilidade acústica relativa entre os diferentes modos de imagem TFM.

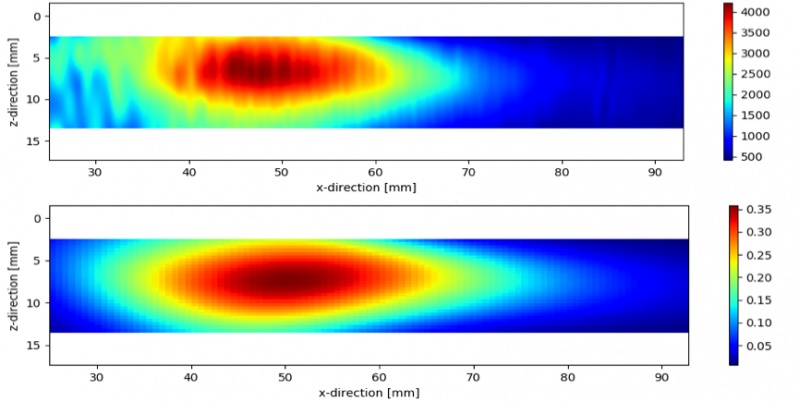
Figura 10: (a) mapa empírico de amplitude da FBH e (b) mapa da sensibilidade da amplitude do FBH para o modo TLT auto-tandem

EXEMPLO DE APLICAÇÃO

Para demonstrar outras utilidades do modelo acústico, apresentamos um exemplo de aplicação no mundo real em que o mapa da sensibilidade da amplitude teórico é usado para guiar a seleção do modo de inspeção TFM. Nesse exemplo, inspecionamos uma amostra de solda com chanfro em V com defeito conhecido de falta fusão. O ângulo da solda é de aproximadamente 35º e usamos a sonda 5L32-A32 e o calço SA32-N55S-IHC, que foram utilizados no experimento de validação da FBH. Um diagrama esquemático da configuração experimental é mostrado na figura 11.

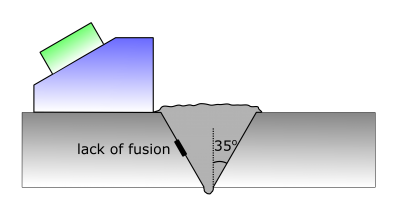
Figura 11: Diagrama esquemático de inspeção de falta de fusão

No modelo teórico, o defeito de falta de fusão é simulado por 5 mm (0,2 pol.) de diâmetro do defeito do FBH que possui superfície inferior orientada a 35º da vertical. O mapa da sensibilidade da amplitude teórico correspondente para o modo TLT auto-tandem e o modo TTTT de salto duplo é mostrado na figura 12.

Figura 12: Objetivo teórico para o plano de inspeção de falta de fusão no (a) modo TLT auto-tandem e (b) no modo TTTT com salto duplo

A figura 12 mostra que o AIM no modo TLT é mais irregular em comparação com o AIM no modo de salto duplo. Consequentemente, seria mais difícil obter uma avaliação sólida do tamanho do defeito de falta de fusão usando o modo TLT. Além disso, a amplitude esperada do modo TLT é três vezes a magnitude mais baixa que no modo de salto duplo. Usando esses mapas de sensibilidade da amplitude teóricos, deduzimos que o modo TTTT de salto duplo é o modo de imagem TFM mais adequado. As imagens TFM experimentais correspondentes são exibidas na figura 13.

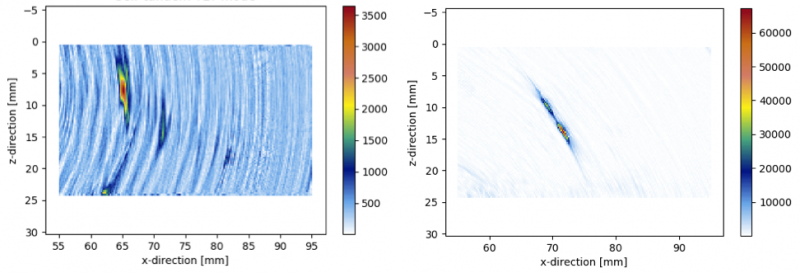
Figura 13: Imagens TFM do defeito de falta de fusão no (a) modo TLT auto-tandem e (b) no modo TTTT de salto duplo

A figura 13 demonstra que a imagem TFM de salto duplo possui uma boa relação sinal-ruído e fornece uma avaliação clara do tamanho do defeito de falta de fusão. Por outro lado, a imagem TFM auto-tandem possui uma relação sinal-ruído ruim e contém ecos isolados que são de difícil interpretação. Os ecos isolados são provavelmente ecos difratados provenientes dos cantos pontiagudos do defeito de falta de fusão. No entanto, o tamanho e o tipo de defeito são difíceis de avaliar no modo TLT auto-tandem.

A baixa relação sinal-ruído da imagem TFM no modo TLT auto-tandem demonstra a baixa amplitude mostrada na AIM teórica na figura 12 (a). No entanto, deve-se notar que a proporção das amplitudes de eco nos dois modos na figura 13 é inferior à proporção de amplitude prevista pelo objetivo teórico AIM da figura 12. Como a geometria do defeito de falta de fusão é diferente do modelo FBH usado para simular a falha, as amplitudes dos ecos difratados dos cantos pontiagudos do defeito de falta de fusão podem ser subestimados no modelo teórico.

CONCLUSÃO

Demonstramos um modelo acústico que pode prever com precisão o mapa de sensibilidade da amplitude do TFM para defeitos não direcionais e direcionais. Para um determinado modo de inspeção, o modelo pode ser usado para ajustar o plano de varredura (abertura, frequência de digitalização, localização da sonda, etc.) para otimizar a relação de sinal-ruído e a probabilidade de detecção. Como o modelo fornece uma comparação da amplitude relativa entre os diferentes modos acústicos, ele também pode ser usado para selecionar o modo de reconstrução TFM ideal. Futuramente, planejamos estender o modelo para geometrias mais complexas e incluir mais modelos de dispersão de falhas para aumentar a utilidade do modelo.

REFERÊNCIAS

[1] C. Holmes, B. W. Drinkwater e P. D. Wilcox, “Post-processing of the full matrix of ultrasonic transmit–receive array data for non-destructive evaluation,” NDT E Int., vol. 38, n° 8, pp. 701–711, dezembro de 2005.

[2] K. Sy, P. Bredif, E. Iakovleva, O. Roy e D. Lesselier, “Development of methods for the analysis of multi-mode TFM images,” J. Phys. Conf. Ser., vol. 1017, p. 012005, maio de 2018.

[3] L. W. S. Jr, Fundamentals of Ultrasonic Nondestructive Evaluation: A Modeling Approach, 2ª ed. Springer International Publishing, 2016.

[4] Foundations of Biomedical Ultrasound. Oxford, New York: Oxford University Press, 2006.

[5] S. I. Nikolov, J. Kortbek e J. A. Jensen, “Practical applications of synthetic aperture imaging,” na 2010 IEEE International Ultrasonics Symposium, San Diego, CA, 2010, pp. 350–358.

[6] E. A. Ginzel e D. Johnson, “Phased-Array Resolution Assessment Techniques,” p. 13.