包络功能使全聚焦方式更出色

Resumo

Este artigo descreve como calcular o envelope de uma imagem do método de foco total (TFM) e as vantagens de se usar o envelope do TFM como parte de uma solução compatível com a norma. O envelope do TFM é obtido calculando a norma de duas imagens diferentes do TFM, a saber, uma primeira imagem TFM calculada usando a FMC (captura de matriz completa adquirida) padrão e uma segunda imagem TFM calculada usando a FMC transformada de Hilbert. A imagem do envelope do TFM resultante fornece uma base melhor para o método de dimensionamento baseado em amplitude, pois é mais resistente à variação de amplitude em comparação com uma imagem oscilatória do TFM padrão em uma resolução de grade idêntica. Portanto, com relação à oscilação do TFM padrão, uma resolução de grade mais espessa pode ser definida para o envelope do TFM, reduzindo, consequentemente, a quantidade total do esforço computacional e, finalmente, aumentando a taxa de aquisição resultante.

Introdução

O método de foco total (TFM) é uma técnica recentemente aceita para avaliação não destrutiva de materiais e estruturas. Certos padrões e códigos agora incluem uma seção sobre captura de matriz completa (FMC) e TFM para testes não destrutivos (END) [1], [2].

Alguns dispositivos END, como o detector de defeitos OmniScan™ X3, permitem a visualização de imagens do TFM em tempo real. A abordagem do TFM usando FMC é resumida na seção a seguir, mas a premissa básica é que o TFM é baseado no somatório de uma infinidade de valores de amplitude elementares de A-scan. As imagens do TFM são oscilatórias devido às origens das ondas acústicas dos A-scans elementares. Por outro lado, os esquemas de caracterização encontrados nas aplicações de END são essencialmente técnicas baseadas em amplitude para os quais o comportamento oscilatório pode ser visto como um artefato acústico supérfluo. Uma prática comum usada para adaptar o comportamento oscilatório aos esquemas de caracterização é retificar a amplitude para que a imagem apareça com valores estritamente positivos. Embora essa abordagem possa facilitar a interpretação da imagem em relação à sua contraparte totalmente oscilante, este artigo mostrará como o uso do envelope de sinal pode melhorar ainda mais o esforço de caracterização e realmente aumentar a taxa de aquisição em relação à imagem do TFM oscilatória padrão.

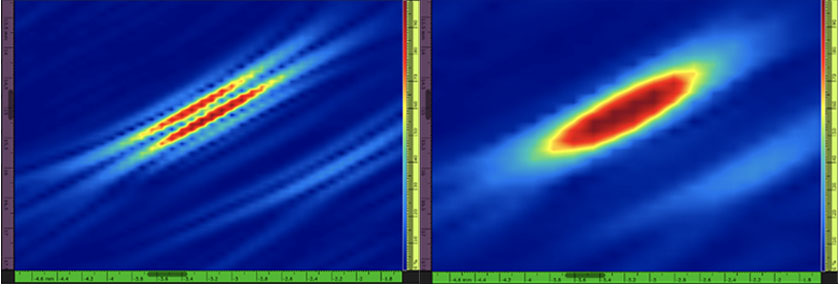
Figura 1 — À esquerda: exemplo de uma imagem do TFM de um furo lateral (SDH) com valores de amplitude estritamente positivos e oscilação de sinal (isto é, TFM padrão). A resolução da grade é de 0,08 mm (λ/8,1) e a amplitude máxima é de 108,7%. À direita: envelope do TFM exatamente do mesmo SDH. A resolução da grade é de 0,16 mm (λ/4,0) e a amplitude máxima é de 122,6%.

Existem várias desvantagens na utilização da imagem oscilatória do TFM. Primeiro, a resolução da grade do TFM — ou seja, a distância entre dois píxeis no quadro — deve ser de aproximadamente λ/8 para ser compatível com a norma [1]—[3]. Neste artigo, λ é o comprimento de onda associado à frequência central e à velocidade acústica da sonda na peça. Uma resolução de grade pequena implica um grande esforço computacional, resultando imediatamente em uma menor taxa de aquisição. A robustez associada aos métodos de dimensionamento de falhas com base na amplitude também é afetada pela oscilação do TFM. De fato, a amplitude máxima de um eco medido depende fortemente do deslocamento de fase do sinal adquirido.

Todos esses problemas podem ser resolvidos usando o envelope do TFM, pois remove as oscilações do sinal na imagem e permite uma medição de amplitude máxima mais robusta (veja Figura 1). A produtividade da aquisição se beneficia do uso do envelope do TFM, pois requer uma resolução de grade reduzida — ou seja, espaçamento maior entre dois píxeis adjacentes — para a mesma robustez de amplitude em comparação com o TFM padrão. Por exemplo, uma resolução de grade de aproximadamente λ/4 é suficiente com o envelope do TFM para ter a mesma fidelidade de amplitude (2 dB) que a oscilação do TFM padrão com uma resolução de λ/8 [3].

O objetivo deste artigo é informar o especialista em END sobre as vantagens da utilização do envelope do TFM. Primeiro, apresentamos uma recapitulação da abordagem FMC-TFM, seguida de uma breve apresentação dos conceitos que envolvem o cálculo do envelope do TFM. Por fim, apresentamos os benefícios do uso do envelope do TFM como parte de uma solução compatível com código em comparação com imagens oscilatórias do TFM padrão.

Resumo da abordagem FMC-TFM

A marca registrada do ultrassom Phased Array é a capacidade de focar em qualquer posição desejada em uma peça que está sendo inspecionada. A abordagem de enfoque Phased Array usa atrasos, tanto na transmissão quanto na recepção, para sincronizar os tempos de voos de sinais curtos e pulsados na posição de interesse. Na zona focal da amostra, a largura total do feixe acústico gerado torna-se pequena e a resolução da detecção correspondente aumenta drasticamente [4]–[12].

O TFM é uma extensão natural dessa capacidade; o TFM produz um feixe focalizado através da focalização e direcionamento do Phased Array em todas as posições em uma região de interesse dentro de uma peça que está sendo inspecionada, e apenas o conjunto de pontos de dados focalizados altamente resolvidos é apresentado ao operador [13]–[16]. Com frequência, a região de interesse consiste em um plano cartesiano uniforme de todos os objetivos de focalização solicitados. Obviamente, alcançar essa focalização em cada posição da grade usando a abordagem de formação de feixe físico convencional seria extremamente demorada devido ao tempo de propagação acústica física necessário para atingir todas as posições de interesse.

Como as ondas acústicas ultrassônicas típicas para aplicações de END são lineares, a formação de feixe físico resultante da superposição de campos acústicos reais para todos os elementos contribuintes de uma determinada abertura pode ser emulada por um processo de pós-aquisição com base nos dados do conjunto de captura de matriz completa (FMC). A recuperação do conjunto de dados FMC requer a gravação do sinal de todos os elementos que compõem a abertura receptora, enquanto uma emissão acústica é produzida por cada elemento individual que compreende a abertura de transmissão. Como tal, o conjunto de dados FMC é formado pela multiplicidade de A-scans elementares para todas as combinações de elementos transmissores e receptores.

Como no Phased Array focalizado convencional, a obtenção da amplitude focalizada de uma determinada posição de focalização requer o seguinte:

• O cálculo do tempo de voo necessário para a propagação acústica atingir a posição focal correspondente a uma posição de grade selecionada de interesse e da volta ao elemento receptor, para todos os pares de elementos de transmissão e recepção da abertura
• A seleção do ponto de dados de amplitude correspondente ao tempo de voo completo de transmissão e recepção apropriado para todos os pares de elementos de transmissão e recepção da abertura
• A soma de todos os pontos de dados de amplitude selecionados sobre todos os elementos contribuintes das aberturas de transmissão e recepção
• O posicionamento da amplitude somada resultante na posição de grade selecionada inicialmente

Repetir essas etapas para todas as posições da grade na região de interesse produz um mapa de amplitude no qual todos os valores de amplitude correspondem a um feixe focalizado, tanto na transmissão quanto na recepção. Esse método de usar os dados FMC para produzir um mapa de amplitude focalizado em cada posição sobre a região de interesse (isto é, a zona do TFM) é referido como abordagem FMC-TFM.

Como o envelope do TFM é calculado

Esta seção descreve como o envelope do TFM é calculado usando os mesmos A-scans elementares (FMC) adquiridos para o TFM padrão. Note que o envelope tem uma manifestação física e não é um mero algoritmo de uniformização de imagem. O envelope na imagem do TFM tem suas raízes nos A-scans individuais constituintes. Primeiro, para ilustrar esquematicamente seu comportamento, o conceito de envelope é apresentado usando uma série temporal de pulso gaussiano. O processo também é aplicado a um A-scan empírico e em um quadro do TFM completo.

O sinal a(t) corresponde ao sinal adquirido — ou seja, o equivalente a um A-scan elementar adquirido através do FMC — e é, de fato, a parte real de um sinal analítico complexo z(t), que pode ser descrito como

onde a’(t) corresponde à parte imaginária do sinal analítico e θ(t) é a fase instantânea do sinal. A parte imaginária é efetivamente calculada usando a transformada de Hilbert [17]. O envelope do sinal corresponde à norma do sinal analítico, que pode ser escrito como

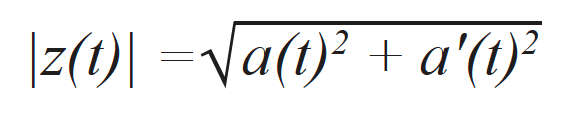
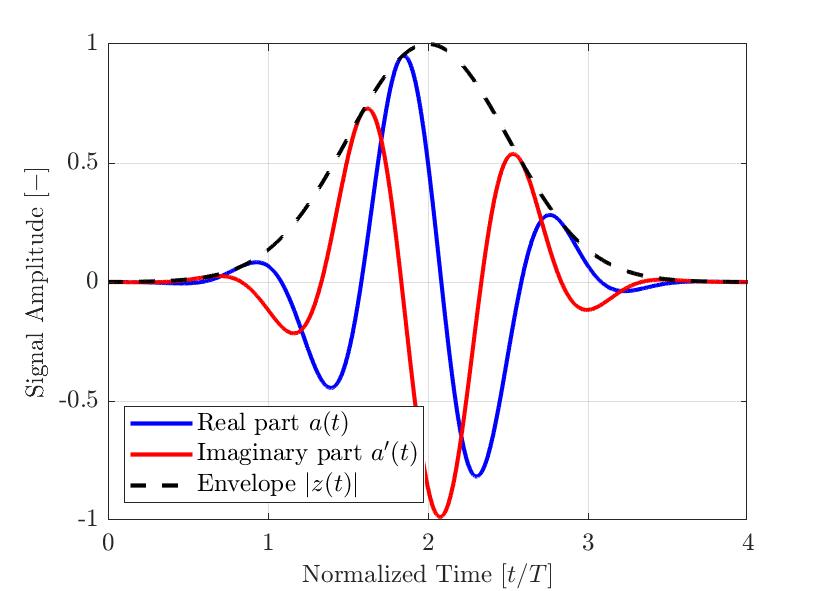
Figura 2 — Um pulso modulado gaussiano típico para aplicações de END. As partes reais e imaginárias e o envelope computado são mostrados. O eixo do tempo é normalizado com o período de frequência central selecionado do pulso.

A Figura 2 mostra um exemplo de um pulso modulado gaussiano simples a(t). O sinal real a(t) está em azul, sua parte imaginária da transformada de Hilbert a’(t) está em vermelho e o envelope resultante |z(t)| é uma linha tracejada. Como visto na equação acima, o envelope de sinal |z(t)| não é afetado pela fase instantânea θ(t) do sinal. Portanto, sinais com diferentes compensações de fase ϕ podem ter o mesmo envelope. A Figura 3 ilustra vários pulsos modulados gaussianos com diferentes deslocamentos de fase ϕ e seu envelope resultante. Portanto, a amplitude máxima medida do sinal é mais robusta quando se usa o envelope do sinal que o valor absoluto do componente real do sinal analítico.

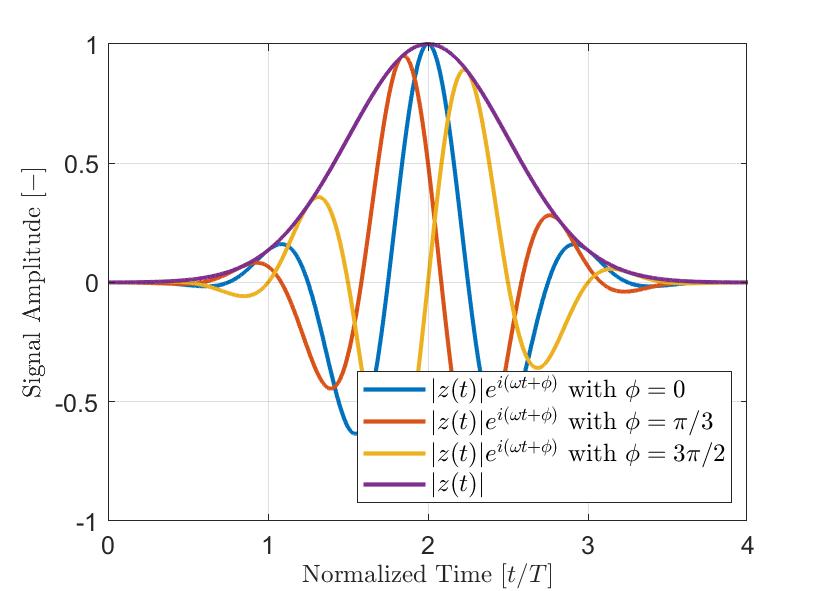
Figura 3 — Pulsos típicos de modulação gaussiana (|z(t)| e ^i(ωt+ϕ)) com diferentes desvios de fase ϕ. O envelope |z(t)| dos sinais é claramente independente da fase instantânea do sinal analítico.

O mesmo processo pode ser usado para obter o envelope de um A-scan empírico. A Figura 4 mostra um A-scan elementar típico adquirido através do FMC, enquanto a Figura 5 mostra o mesmo A-scan (azul) com sua transformada de Hilbert (vermelho) e o envelope calculado (linha tracejada). Todos os sinais mostrados são normalizados ao máximo do envelope de amplitude.

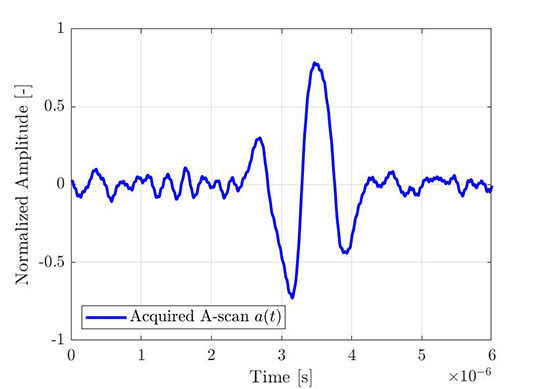Figura 4 — Parte de um A-scan elementar adquirido (de uma aquisição FMC).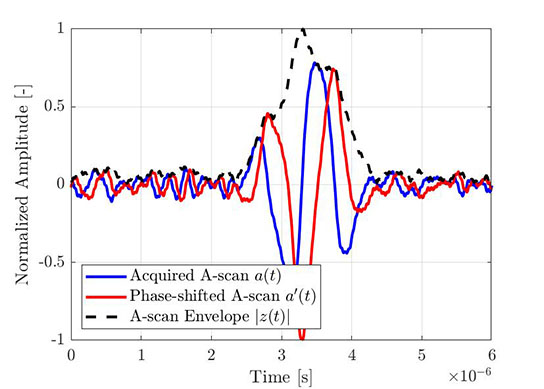

Figura 5 — O mesmo A-scan elementar com sua transformada de Hilbert e o envelope computado.

A imagem do envelope do TFM — com índices de pontos de grade individuais (k, l) — é calculada usando os sinais analíticos de todos os seus A-scans associados [15]. De fato, é o resultado do cálculo da norma de uma imagem analítica do TFM y(k,l) composta pelo quadro do TFM padrão x(k,l) calculado usando os dados adquiridos FMC padrão e um quadro do TFM x’(k,l) computado com a transformada de Hilbert dos dados FMC. O mesmo conjunto de atrasos é usado nos dois casos. O envelope do TFM é então calculado usando a seguinte expressão

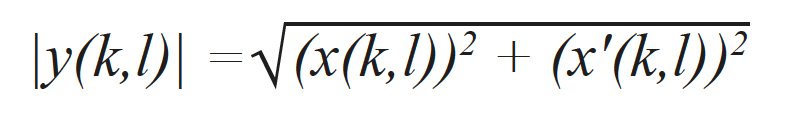
Uma imagem de envelope do TFM é, portanto, o resultado de uma combinação de duas imagens do TFM (veja a Figura 6): uma do componente real dos A-scans elementares e a outra do componente imaginário calculado com os A-scans elementares. Embora esse processo aumente a carga computacional e reduza a velocidade de aquisição do instrumento END, demonstramos na próxima seção que a resolução da grade necessária pode ser reduzida significativamente sem afetar a fidelidade da amplitude, aumentando a velocidade de aquisição para uma taxa mais alta do que ao usar o TFM padrão.

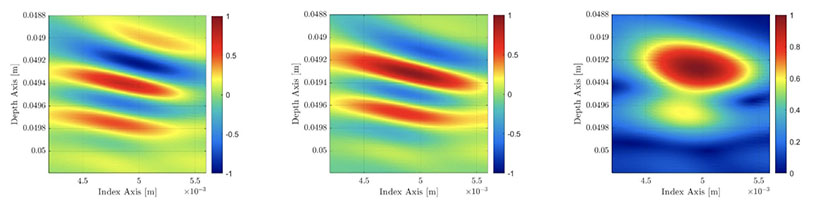
Figura 6 — Esquerda: quadro do TFM padrão (não no valor absoluto). Centro: quadro do TFM calculado usando a transformada de Hilbert da captura completa da matriz. Direita: imagem resultante do envelope do TFM.

Vantagens da utilização do envelope do TFM

Nesta seção, demonstramos as vantagens do envelope do TFM comparando vários quadros do TFM com diferentes taxas de resolução de grade, variando de λ/9,3 a λ/4,0, e monitorando várias métricas críticas de inspeção. Os resultados foram obtidos usando uma sonda 5L32-A31 e um calço SA31-N55S-IHC em um bloco de aço com um furo lateral de 1 mm de diâmetro (SDH) (veja a Figura 7). Um gel de acoplamento (Sonotech Ultragel II) é usado entre o calço e o bloco de aço. Os dados são adquiridos usando o detector de defeitos OmniScan™ X3, da Olympus. O trajeto acústico do pulso-eco (T-T) é selecionado e o tamanho da zona é de 20 mm × 20 mm. O comprimento de onda associado à peça e ao caminho acústico selecionado é λ = 0,648 mm. A resolução da grade é anotada em termos da fração do comprimento de onda.

Figura 7 — Uma foto da configuração usada para adquirir as imagens do TFM na Tabela 1. O retângulo azul corresponde a toda a região de interesse (20 mm × 20 mm) enquanto o retângulo vermelho corresponde à região de interesse ampliada (5 mm × 5 mm) mostrado nas imagens da Tabela 1. Utilizamos uma sonda 5L32-A31 e um calço SA31-N55S-IHC. O bloco de aço tem espessura de 40 mm.

A Tabela 1 mostra as imagens do TFM resultantes para quatro valores diferentes de resolução de grade, variando de λ/9,3 a λ/4,0, tanto para o envelope padrão do TFM quanto para o TFM. O valor da fidelidade da amplitude calculada [3] e a taxa de aquisição resultante são indicados em cada uma das imagens do TFM.

Resolução da grade	TFM padrão	Envelope TFM
λ/9,3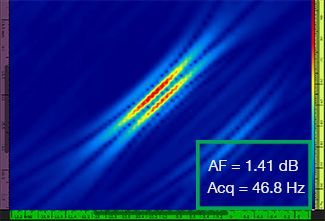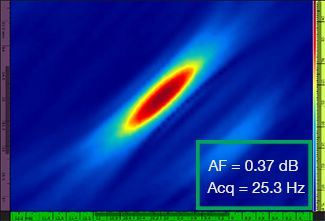
λ/8,1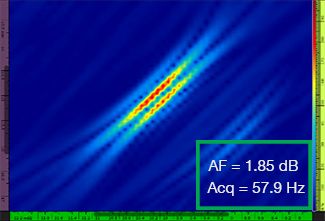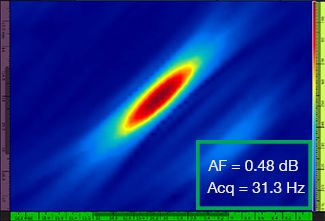
λ/5,9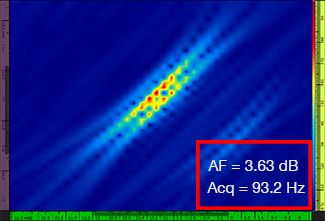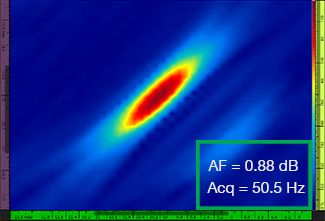
λ/4,0

Os códigos e padrões recentemente disponíveis [1, 2] exigem que o valor da fidelidade da amplitude seja de 2 dB ou menos. Portanto, apenas os dois primeiros valores de resolução da grade (λ/9,3, λ/8,1) são compatíveis com a norma ao usar o TFM padrão. O envelope do TFM permite uma resolução de grade mais espessa (λ/4,0), mantendo uma fidelidade de amplitude compatível com a norma. Por sua vez, o uso do envelope do TFM com uma grade mais espessa induz um aumento na velocidade de aquisição de aproximadamente 37% em relação à maior taxa de aquisição alcançada pelo padrão do TFM em conformidade com a norma (57,9 Hz em λ/8,1).

Conclusão

O método para calcular o envelope de uma imagem do TFM foi apresentado e ilustrado usando exemplos simples. Demonstramos que o envelope de um sinal é independente de sua fase instantânea e, portanto, fornece uma base mais robusta para técnicas de dimensionamento baseadas em amplitude (como o método de queda de 6 dB). O envelope de sinal não é meramente uma uniformização da imagem e não deve ser considerado como um filtro, que pode gerar perdas de dados. As vantagens de se usar o envelope na imagem do TFM foram demonstradas através de comparações de imagens do TFM, com e sem o envelope, para diferentes valores de resolução da grade. Embora duas imagens do TFM devam ser calculadas para obter o envelope do TFM resultante, a carga de processamento pode ser reduzida significativamente usando uma resolução de grade mais grossa, mantendo a conformidade com a norma. Isso se deve à robustez do envelope em relação à variação de amplitude. O resultado é uma imagem mais adaptada ao dimensionamento da amplitude, mas obtida em um ritmo mais rápido que a imagem equivalente processada usando o TFM padrão.

Referências

[1] ASME Committee, “ASME BPVC.V Article 4 Mandatory Appendix XI Full Matric Capture.” ASME, 2019.

[2] ASME Committee, “ASME BPVC.V Article 4 Nonmandatory Appendix F — Examination of Welds Using Full Matric Capture.” ASME, 2019.

[3] N. Badeau, A. Le Duff, and C.-H. Kwan, “Theoretical Model for Amplitude Fidelity Reading (submitted),” apresentado no ASNT Research Symposium, 2020.

[4] A. C. Clay, S.-C. Wooh, L. Azar e J.-Y. Wang, “Experimental Study of Phased Array Beam Steering Characteristics,” Journal of Nondestructive Evaluation, vol. 18, no. 2, p. 13, 1999.

[5] L. J. Bond, “Fundamentals of Ultrasonic Inspection,” ASM Handbook, vol. 17, no. Nondestructive Evaluation of Material, pp. 155–168, 2018.

[6] S.-J. Song, H. J. Shin, and Y. H. Jang, “Development of an ultra sonic phased array system for nondestructive tests of nuclear power plant components,” Nuclear Engineering and Design, vol. 214, no. 1–2, pp. 151–161, maio de 2002, doi: 10.1016/S0029-5493(02)00024-9.

[7] S. Mahaut, O. Roy, C. Beroni e B. Rotter, “Development of phased array techniques to improve characterization of defect located in a component of complex geometry,” Ultrasonics, vol. 40, no. 1–8, pp. 165–169, maio de 2002, doi: 10.1016/S0041-624X(02)00131-2.

[8] S. C. Mondal, P. D. Wilcox, and B. W. Drinkwater, “Design of Two-Dimensional Ultrasonic Phased Array Transducers,” Journal of Pressure Vessel Technology, vol. 127, no. 3, pp. 336–344, agosto de 2005, doi: 10.1115/1.1991873.

[9] S.-C. Wooh and Y. Shi, “Influence of phased array element size on beam steering behavior,” Ultrasonics, vol. 36, no. 6, pp. 737–749, abril de 1998, doi: 10.1016/S0041-624X(97)00164-9.

[10] Joon-Hyun Lee and Sang-Woo Choi, “A parametric study of ultrasonic beam profiles for a linear phased array transducer,” IEEE Trans. Ultrason., Ferroelect., Freq. Contr., vol. 47, no. 3, pp. 644–650, maio de 2000, doi: 10.1109/58.842052.

[11] R. Ahmad, T. Kundu, and D. Placko, “Modeling of phased array transducers,” The Journal of the Acoustical Society of America, vol. 117, no. 4, pp. 1762–1776, abril de 2005, doi: 10.1121/1.1835506.

[12] B. W. Drinkwater and P. D. Wilcox, “Ultrasonic arrays for non-destructive evaluation: A review,” NDT & E International, vol. 39, no. 7, pp. 525–541, outubro de 2006, doi: 10.1016/j.ndteint.2006.03.006.

[13] P. D. Wilcox, “Exploiting the Full Data Set from Ultrasonic Arrays by Post-Processing,” in AIP Conference Proceedings, Brunswick, Maine (USA), 2006, vol. 820, pp. 845–852, doi: 10.1063/1.2184614.

[14] J. Zhang, B. W. Drinkwater, and P. D. Wilcox, “Effects of array transducer inconsistencies on total focusing method imaging performance,” NDT & E International, vol. 44, no. 4, pp. 361–368, julho de 2011, doi: 10.1016/j.ndteint.2011.03.001.

[15] C. Holmes, B. W. Drinkwater, and P. D. Wilcox, “Advanced post-processing for scanned ultrasonic arrays: Application to defect detection and classification in non-destructive evaluation,” Ultrasonics, vol. 48, no. 6–7, pp. 636–642, novembro de 2008, doi: 10.1016/j.ultras.2008.07.019.

[16] C. Holmes, B. W. Drinkwater, and P. D. Wilcox, “Post-processing of the full matrix of ultrasonic transmit–receive array data for non-destructive evaluation,” NDT & E International, vol. 38, no. 8, pp. 701–711, dezembro de 2005, doi: 10.1016/j.ndteint.2005.04.002.

[17] D. Gabor, “Theory of Communication,” Journal of the Institution of Electrical Engineers, vol. 96, pp. 429–441, 1946.